Teil B – Pflichtaufgaben
Aufgabe 1
Die Geschwister Jule, Paul und Anton verfügen jeder über ein Sparbuch. Der Zinssatz für das Jahr 2015 ist für alle drei Sparbücher gleich und beträgt  pro Jahr.
pro Jahr.
Die Zinsen für die Spareinlagen werden immer zum 31. Dezember des jeweiligen Kalenderjahres gutgeschrieben.
Die Zinsen für die Spareinlagen werden immer zum 31. Dezember des jeweiligen Kalenderjahres gutgeschrieben.
a)
Jule zahlte am 1. Mai 2015 einen Betrag von  auf ihr Sparbuch ein.
auf ihr Sparbuch ein.
Berechne die Zinsen, die sie bis zum Jahresende für diesen Betrag erhielt.
Berechne die Zinsen, die sie bis zum Jahresende für diesen Betrag erhielt.
b)
Paul legte für das gesamte Jahr 2015 einen bestimmten Betrag auf seinem Sparbuch an.
Er erhielt am Ende des Jahres dafür Zinsen gutgeschrieben.
Zinsen gutgeschrieben.
Berechne die Höhe des angelegten Betrages.
Er erhielt am Ende des Jahres dafür
Berechne die Höhe des angelegten Betrages.
c)
Anton hatte 2015 für einige Monate einen Betrag von  auf seinem Sparbuch angelegt. Er erhielt dafür
auf seinem Sparbuch angelegt. Er erhielt dafür  Zinsen.
Zinsen.
Ermittle, wie viel Monate Anton diesen Betrag auf seinem Sparbuch hatte.
Ermittle, wie viel Monate Anton diesen Betrag auf seinem Sparbuch hatte.
Für Aufgabe 1 erreichbare BE: 6
Aufgabe 2
Gegeben ist die Funktion  durch die Gleichung
durch die Gleichung 
a)
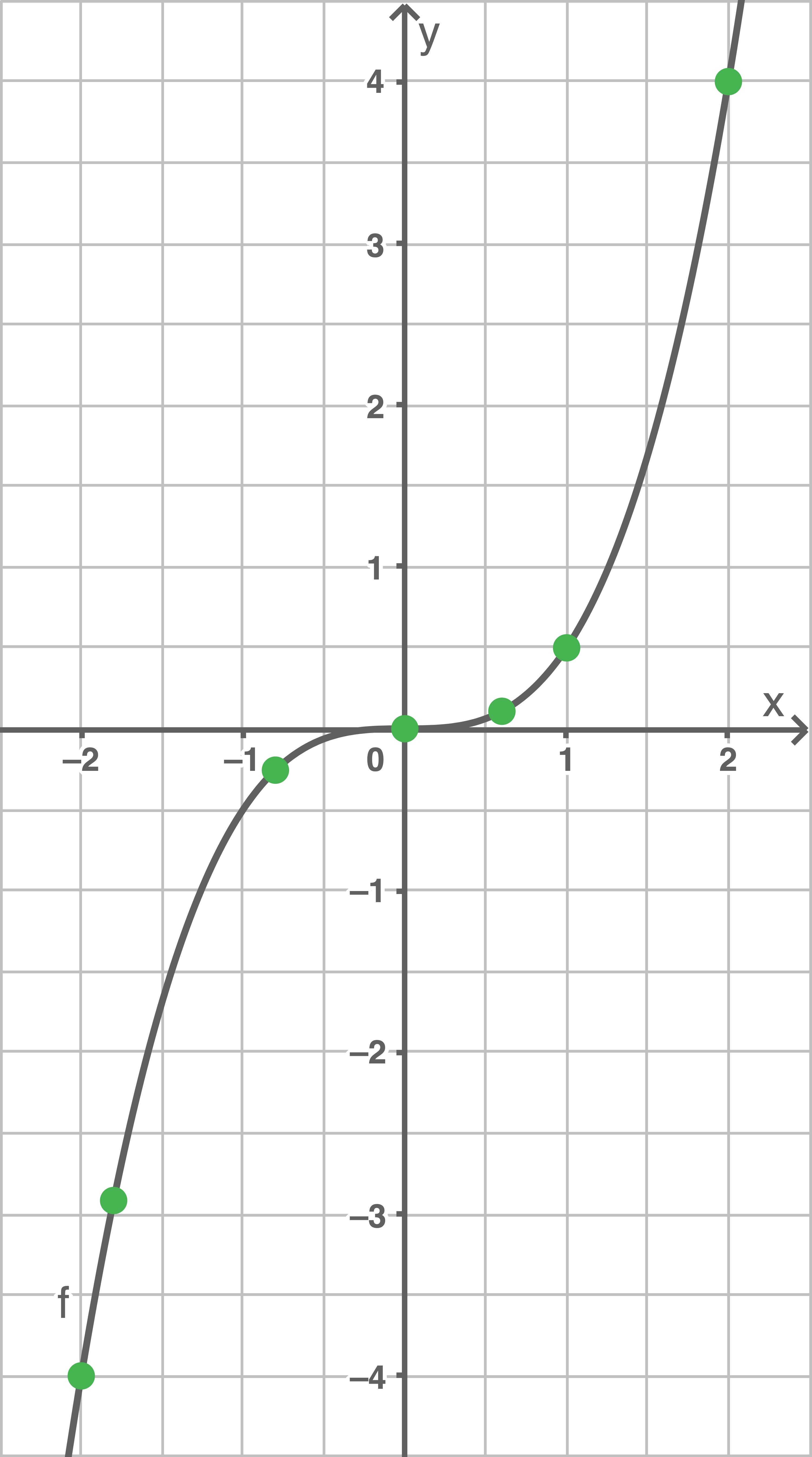
Übernimm die Wertetabelle und vervollständige diese.
Zeichne den Graphen der Funktion  mindestens im Intervall
mindestens im Intervall  in ein rechtwinkliges Koordinatensystem.
in ein rechtwinkliges Koordinatensystem.
b)
Der Punkt  liegt auf dem Graphen einer Funktion
liegt auf dem Graphen einer Funktion 
Gib den Wert für an.
an.
Gib den Wert für
Für Aufgabe 2 erreichbare BE: 5
Aufgabe 3
Für eine Gartenschau wird ein altes Bahnhofsgelände umgestaltet. Dazu gehört auch der Platz mit der ehemaligen Drehscheibe.
Der Platz kann als zusammengesetzte Fläche aus einem Parallelogramm und einem Trapez betrachtet werden (siehe Abbildung).
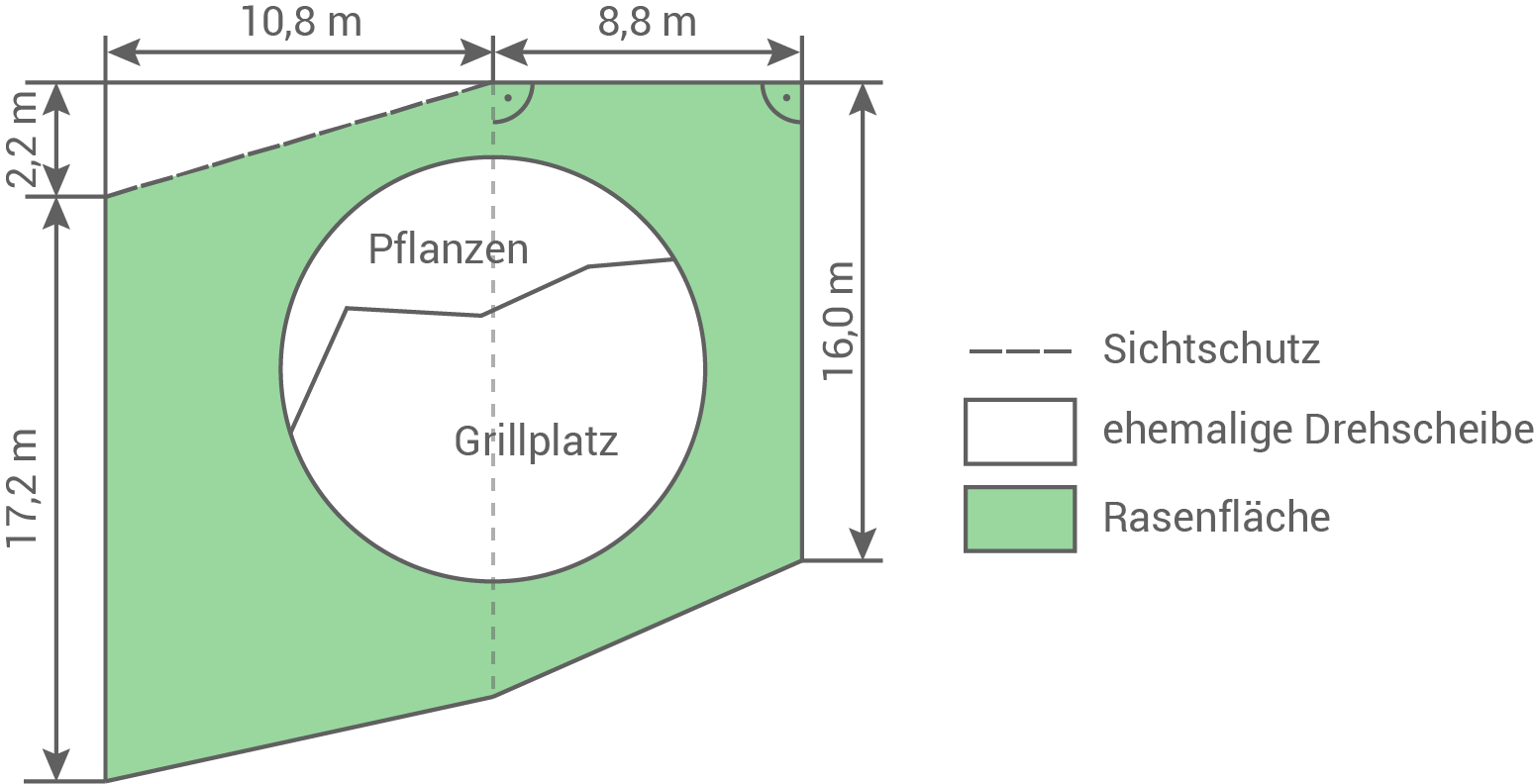 Die ehemalige Drehscheibe hat einen Flächeninhalt von
Die ehemalige Drehscheibe hat einen Flächeninhalt von 

Abbildung (nicht maßstäblich)
a)
Bepflanzt werden  der ehemaligen Drehscheibe. Pro Quadratmeter plant der Gärtner fünf Pflanzen.
der ehemaligen Drehscheibe. Pro Quadratmeter plant der Gärtner fünf Pflanzen.
Berechne, wie viele Pflanzen der Gärtner einplanen muss.
Berechne, wie viele Pflanzen der Gärtner einplanen muss.
b)
Als Sichtschutz wird eine hohe Hecke gepflanzt.
Berechne die Länge des Sichtschutzes.
Berechne die Länge des Sichtschutzes.
c)
Um die ehemalige Drehscheibe wird eine Rasenfläche angelegt.
Berechne den Flächeninhalt der Rasenfläche.
Berechne den Flächeninhalt der Rasenfläche.
Für Aufgabe 3 erreichbare BE: 7
Aufgabe 4
Ilja untersucht im Rahmen eines Projektes seine tägliche Fahrzeit zur Schule.
Er notiert die Fahrzeiten von zwei Schulwochen der Reihe nach und erhält die folgende Urliste: 23 min; 25 min; 23 min; 24 min; 23 min;
23 min; 48 min; 34 min; 23 min; 54 min
Er notiert die Fahrzeiten von zwei Schulwochen der Reihe nach und erhält die folgende Urliste: 23 min; 25 min; 23 min; 24 min; 23 min;
23 min; 48 min; 34 min; 23 min; 54 min
a)
Berechne das arithmetische Mittel der Fahrzeiten.
b)
Ermittle den Zentralwert der Fahrzeiten.
c)
Gib den Modalwert der Fahrzeiten an.
d)
Ilja hat die Fahrzeiten in einem Diagramm dargestellt.
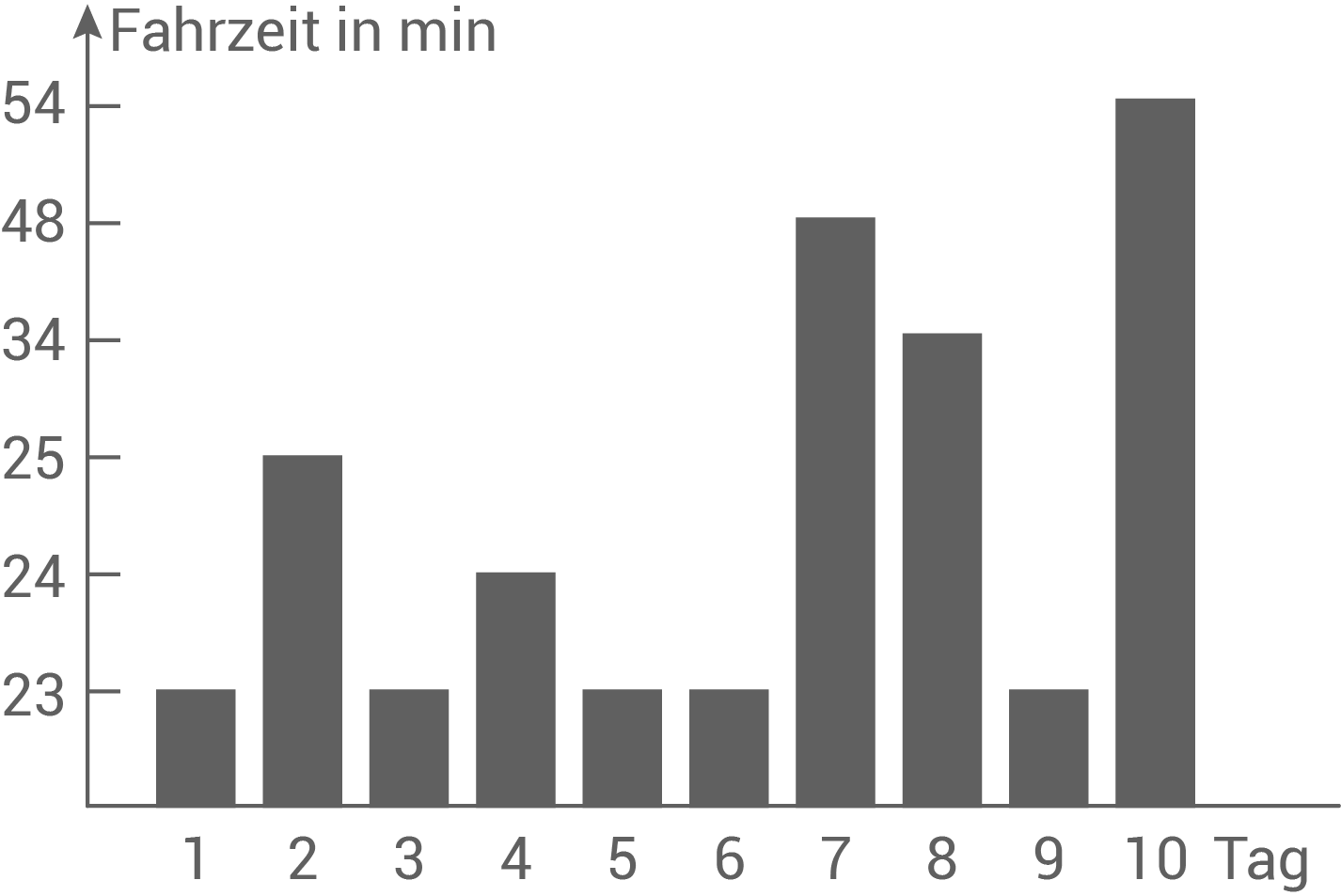 Begründe, warum dieses Diagramm den Sachverhalt falsch veranschaulicht.
Begründe, warum dieses Diagramm den Sachverhalt falsch veranschaulicht.

Für Aufgabe 4 erreichbare BE: 6
Aufgabe 5
Gold ist eine Wertanlage. Man kann es in Barren oder Münzen verschiedener Größen erwerben. Ein Kubikzentimeter Gold hat eine Masse von  Gramm.
Gramm.
a)
Ein Goldbarren hat eine Masse von 
- Berechne das Volumen dieses Goldbarrens auf hundertstel Kubikzentimeter genau.
- Dieser Goldbarren wird zu einem Tagespreis von
gehandelt.
Gib an, für wie viel Euro ein Kubikzentimeter Gold an diesem Tag gehandelt wird.
b)
Ein anderer Goldbarren hat ein Volumen von 
Aus ihm sollen gleiche, zylinderförmige Goldmünzen mit einem Durchmesser von
gleiche, zylinderförmige Goldmünzen mit einem Durchmesser von  gegossen werden.
gegossen werden.
 Berechne die Höhe einer solchen Goldmünze in Millimeter.
Berechne die Höhe einer solchen Goldmünze in Millimeter.
Aus ihm sollen

Für Aufgabe 5 erreichbare BE: 6
Lösung 1
a)
Zinsen für ein Jahr berechnen
 Monaten.
Monaten.




![\(\begin{array}{rcl}
12 & \mathrel{\widehat{=}}& 5,85\,€\\[5pt]
1& \mathrel{\widehat{=}}& \dfrac{5,85}{12}\,€\\[5pt]
8& \mathrel{\widehat{=}}& \dfrac{5,85}{12}\cdot 8\,€
\end{array}\)](https://www.schullv.de/resources/formulas/d75d42f23fefad80576ddeca1dba7907eb024804f6fbf8dd3a9a92c6e893c496_light.svg)




 Jule erhielt
Jule erhielt  Zinsen.
Zinsen.
Lösungsweg über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 650\,€\\[5pt]
1\,\% & \mathrel{\widehat{=}}& \dfrac{650}{100}\,€\\[5pt]
0,90\,\% & \mathrel{\widehat{=}}& \dfrac{650}{100}\cdot 0,90\,€
\end{array}\)](https://www.schullv.de/resources/formulas/8c6c0ca6f643aa742d0310511ea11d3be2c8b5a17a0dc4e396f7b990902de87a_light.svg)





Lösungsweg über die Verhältnisformel
![\(\begin{array}[t]{rll}
\dfrac{x}{0,90\,\%}&=&\dfrac{650\,€}{100\,\%} &\quad \scriptsize \mid\;\cdot 0,90\,\% \\[5pt]
x&=&\dfrac{650\,€}{100\,\%}\cdot 0,90\,\% \\[5pt]
x&=&5,85\,€
\end{array}\)](https://www.schullv.de/resources/formulas/d2847404cbdc8f37eabf77245bdb6f53c4355048c5ad85474ec3ae6911fa3acc_light.svg)
Lösungsweg über die Zinsformel
![\(\begin{array}[t]{rll}
Z&=&\dfrac{K\cdot p}{100} \\[5pt]
Z&=&\dfrac{650\,€\cdot 0,90}{100} \\[5pt]
Z&=&5,85\,€
\end{array}\)](https://www.schullv.de/resources/formulas/2c5bb085648104c32d464368ea7e72025d32d02919e0864a97f6fe9fd41b467b_light.svg)
Lösungsweg über den Dezimalbruch

Zinsen für den Zeitraum 01.05. bis 31.12. berechnen
Dieser Zeitraum besteht aus
b)
Die Höhe des angelegten Betrags kann wieder über den Dreisatz, die Verhältnisgleichung, die Zinsformel oder den Dezimalbruch berechnet werden.
Beispielhafter Lösungsweg über die Zinsformel
![\(\begin{array}[t]{rll}
K&=& \dfrac{Z\cdot 100}{p} \\[5pt]
K&=& \dfrac{4,23\,€ \cdot 100}{0,90} \\[5pt]
K&=& \underline{\underline{ 470,00\,€ }}
\end{array}\)](https://www.schullv.de/resources/formulas/2c8488190ab5468a20dbba3d475b3074aef39abed9859878ba84dd9b0af527d4_light.svg) Paul hat
Paul hat  angelegt.
angelegt.
c)
Zunächst werden die Zinsen für ein Jahr benötigt. Diese können wieder über den Dreisatz, die Verhältnisgleichung, die Zinsformel oder den Dezimalbruch berechnet werden.
Beispielhafter Lösungsweg über die Zinsformel
![\(\begin{array}[t]{rll}
Z&=& \dfrac{K\cdot p}{100} \\[5pt]
Z&=& \dfrac{550\,€\cdot 0,90}{100} \\[5pt]
Z&=& 4,95\,€
\end{array}\)](https://www.schullv.de/resources/formulas/9197d6cfcc5918737360e7d7bff1656a35f57f9d221714acdfc001cc84cb105b_light.svg) Damit kann die Anzahl der Monate berechnet werden:
Beispielhafter Lösungsweg über den Dreisatz
Damit kann die Anzahl der Monate berechnet werden:
Beispielhafter Lösungsweg über den Dreisatz




![\(\begin{array}{rcl}
4,95\,€ & \mathrel{\widehat{=}}& 12\\[5pt]
1\,€ & \mathrel{\widehat{=}}& \dfrac{12}{4,95}\\[5pt]
1,65\,€ & \mathrel{\widehat{=}}& \dfrac{12}{4,95}\cdot 1,65\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/674e7010c753a5060acd7f6f5592c79b8bd9afce842c7eb0074c3a04104fd19e_light.svg)




 Anton hatte 2015 für
Anton hatte 2015 für  Monate sein Geld angelegt.
Monate sein Geld angelegt.
Lösung 2
a)
Wertetabelle übernehmen und vervollständigen
Graphen der Funktion zeichnen

b)
Um den Wert für  anzugeben, werden die
anzugeben, werden die  - und
- und  -Koordinate von
-Koordinate von  in die Funktionsgleichung eingesetzt:
in die Funktionsgleichung eingesetzt:
![\(\begin{array}[t]{rll}
y&=&ax^3 \\[5pt]
4&=&a\cdot 1^3 \\[5pt]
a&=&\underline{\underline{ 4}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/cf57d35166e7ec9134923954136488d4856f5e414996652456833ff5dd193b8b_light.svg) Der Wert für
Der Wert für  lautet
lautet 
Lösung 3
a)
Zunächst wird die Fläche, die bepflanzt wird, in Quadratmeter benötigt. Diese kann über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.
Beispielhafter Lösungsweg über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 123\,\text{m}^2\\[5pt]
1\,\% & \mathrel{\widehat{=}}& \dfrac{123}{100}\,\text{m}^2\\[5pt]
26\,\% & \mathrel{\widehat{=}}& \dfrac{123}{100}\cdot 26\,\text{m}^2\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7664ac8e4b58e68934123a5537dd6485d4034e7185c44fe91466ec3ecfc1724a_light.svg)




 Damit kann die Anzahl der Pflanzen berechnet werden:
Damit kann die Anzahl der Pflanzen berechnet werden:
 Der Gärtner muss
Der Gärtner muss  Pflanzen einplanen.
Pflanzen einplanen.
b)
Satz des Pythagoras anwenden:
![\(\begin{array}[t]{rll}
c^2&=&(10,8\,\text{m})^2+(2,2\,\text{m})^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
c&=&\sqrt{(10,8\,\text{m})^2+(2,2\,\text{m})^2} \\[5pt]
c&\approx&\underline{\underline{ 11,0\,\text{m}}}
\end{array}\)](https://www.schullv.de/resources/formulas/0fbb138e9b0e1a14f7f27ffb1abc11a200cbf686f8d8c4b41676b41ffacf1ccd_light.svg) Die Länge des Sichtschutzes beträgt etwa
Die Länge des Sichtschutzes beträgt etwa 
c)
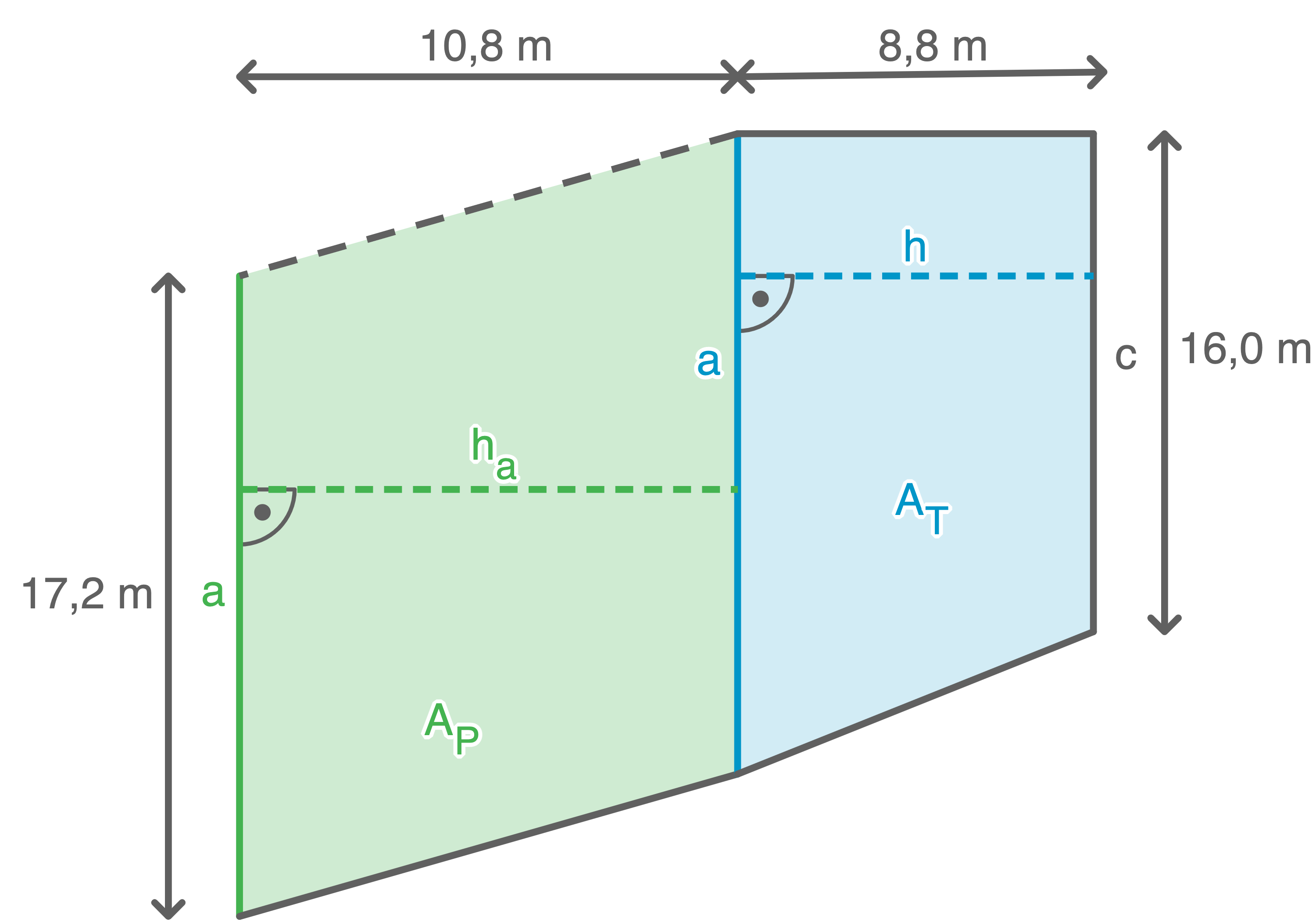
Lösung 4
a)
b)
Um den Zentralwert zu ermitteln, werden die Fahrzeiten zunächst der Größe nach sortiert:
Da die Liste eine gerade Anzahl an Werten beinhaltet, werden die beiden Werte in der Mitte addiert und das Ergebnis durch zwei geteilt:

c)
Der Modalwert ist der Wert, der am häufigsten vorkommt.

d)
Die Höhen der Säulen entsprechen nicht den Größen der Daten aus der Urliste. Grund dafür ist die falsche Einteilung der  -Achse: Sie beginnt nicht bei
-Achse: Sie beginnt nicht bei  und die Abstände sind nicht regelmäßig. Dadurch veranschaulicht das Diagramm den Sachverhalt falsch.
und die Abstände sind nicht regelmäßig. Dadurch veranschaulicht das Diagramm den Sachverhalt falsch.
Lösung 5
a)
Volumen des Goldbarrens auf hundertstel Kubikzentimeter genau berechnen
 Das Volumen des Goldbarrens beträgt etwa
Das Volumen des Goldbarrens beträgt etwa  Für wie viel Euro wird ein Kubikzentimeter Gold an diesem Tag gehandelt?
Für wie viel Euro wird ein Kubikzentimeter Gold an diesem Tag gehandelt?
 An diesem Tag wird ein Kubikzentimeter Gold für
An diesem Tag wird ein Kubikzentimeter Gold für  gehandelt.
gehandelt.
b)
Volumen einer Münze berechnen
 Flächeninhalt der kreisförmigen Grundfläche einer Münze berechnen
Flächeninhalt der kreisförmigen Grundfläche einer Münze berechnen
![\(\begin{array}[t]{rll}
A_G&=&\pi\cdot r^2 \\[5pt]
A_G&=&\pi\cdot \left(\dfrac{d}{2}\right)^2 \\[5pt]
A_G&=&\pi\cdot \left(\dfrac{3,28\,\text{cm}}{2}\right)^2 \\[5pt]
A_G&\approx&8,45\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/3bfdccc9f3384fb94997a2ba92f193d7ef9d5e62e102058d86f4b772afbc3443_light.svg) Höhe einer Münze berechnen
Höhe einer Münze berechnen
![\(\begin{array}[t]{rll}
V&=&A_G\cdot h &\quad \scriptsize \mid\;:A_G \\[5pt]
\dfrac{V}{A_G}&=&h\\[5pt]
h&=&\dfrac{V}{A_G} \\[5pt]
h&=&\dfrac{2,2\,\text{cm}^3}{8,45\,\text{cm}^2 } \\[5pt]
h&\approx&0,26\,\text{cm} \\[5pt]
h&=&\underline{\underline{ 2,6\,\text{mm}}}
\end{array}\)](https://www.schullv.de/resources/formulas/1ab45393d2f2d9b51aaac04fad1882d5c192d88289c990f078260d034f3636ea_light.svg) Die Höhe einer Goldmünze beträgt etwa
Die Höhe einer Goldmünze beträgt etwa 