Teil A – Arbeitsblatt
1.
a)
b)
c)
d)
2.
Im Erzgebirge steht der längste Tisch aus nur einem Baumstamm.
Der Tisch ist lang. An dem Tisch saßen zur Einweihung
lang. An dem Tisch saßen zur Einweihung  Erwachsene gleichzeitig.
Erwachsene gleichzeitig.
Schätze, wie viel Platz jeder am Tisch hatte.
Der Tisch ist
Schätze, wie viel Platz jeder am Tisch hatte.

3.
Wahr oder falsch? Kreuze an.
| wahr | falsch | |
| Die Funktion |
||
| Zwischen den Zahlen |
4.
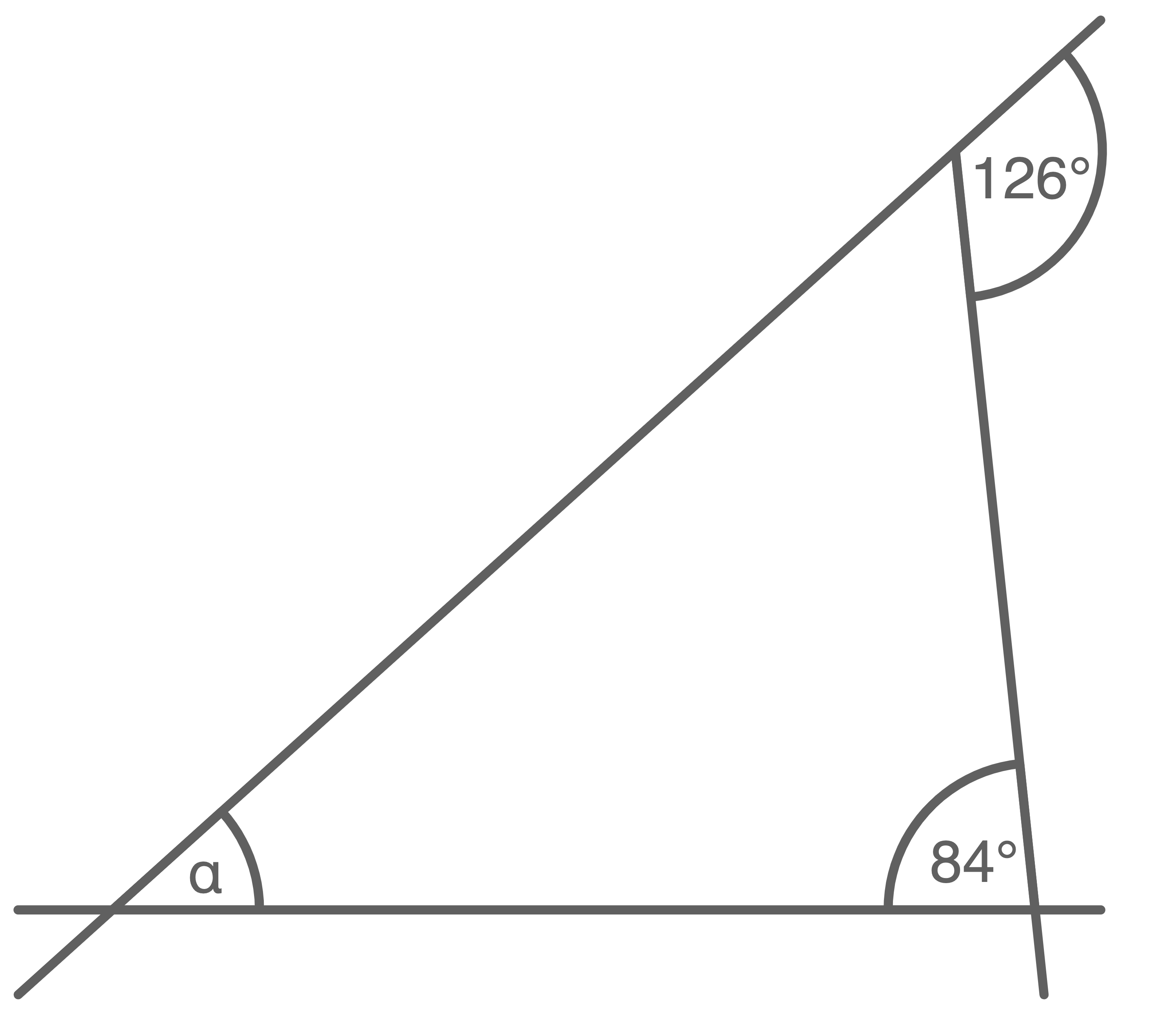
Abbildung (nicht maßstäblich)
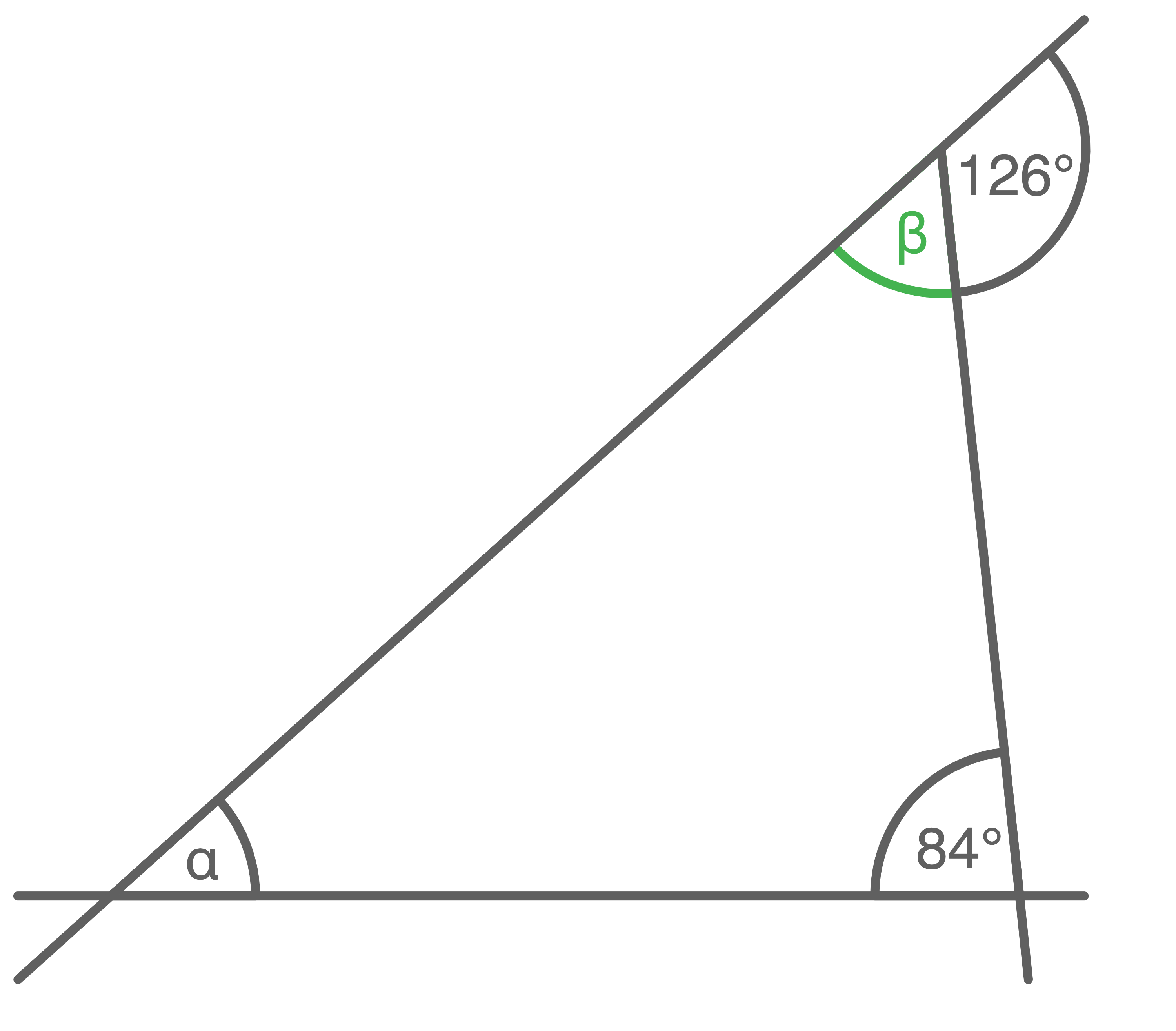
Gib die Größe des Winkels  an.
an.
5.
Markiere und beschrifte  auf der Zahlengerade.
auf der Zahlengerade.


6.
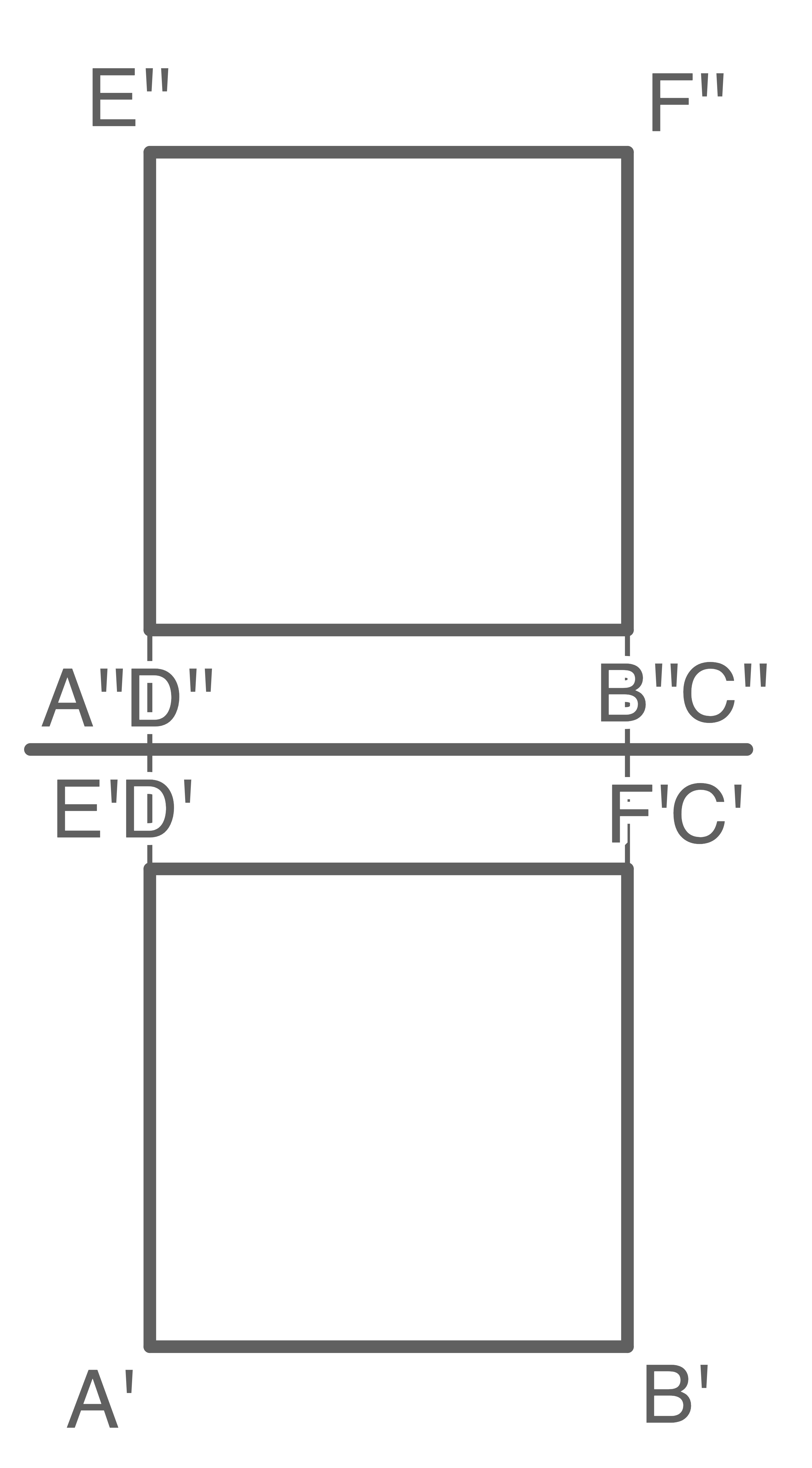
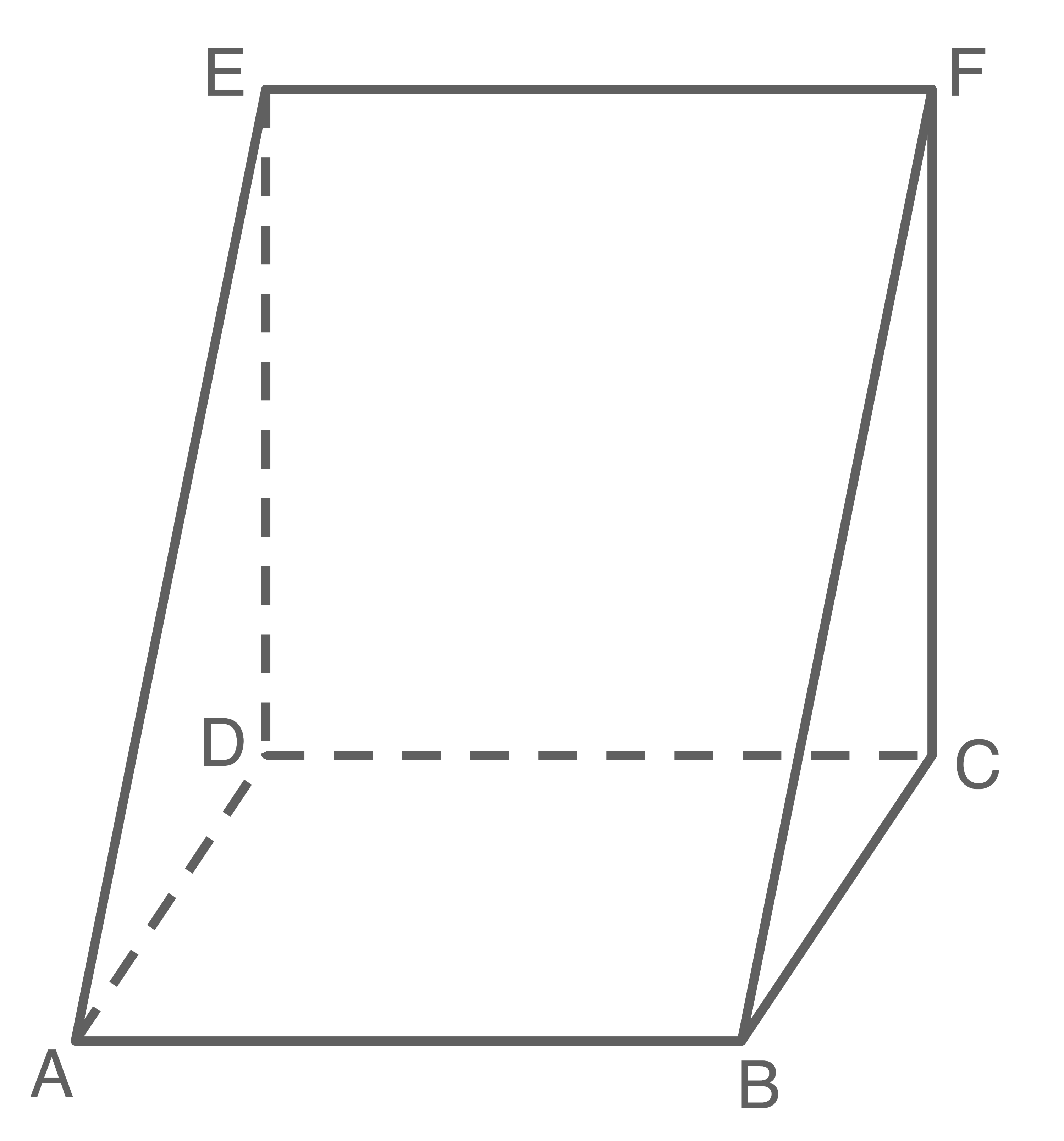
Im senkrechten Zweitafelbild ist ein Prisma dargestellt.
Beschrifte im Schrägbild die Eckpunkte dieses Prismas.
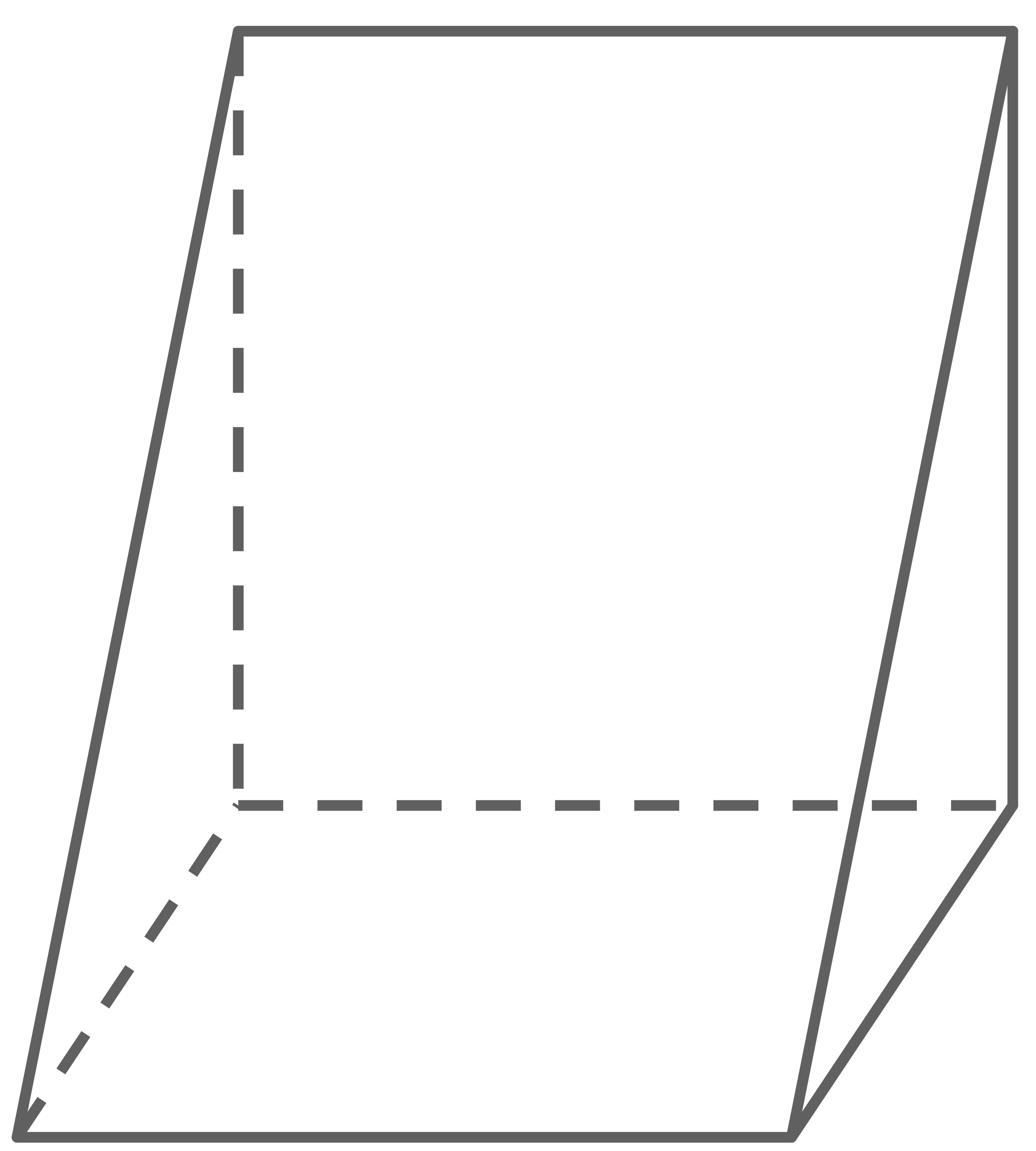
Beschrifte im Schrägbild die Eckpunkte dieses Prismas.

7.
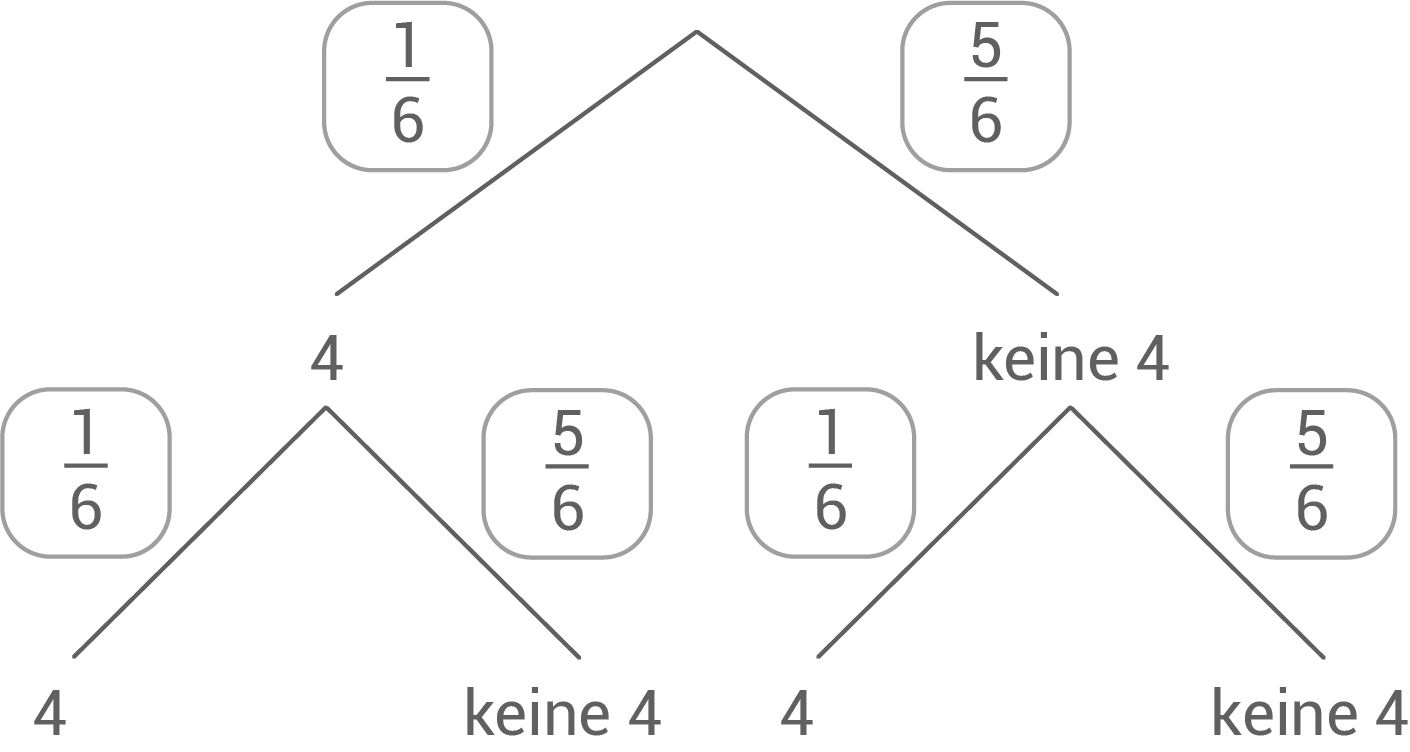
Ein idealer Würfel mit den Augenzahlen eins bis sechs wird zweimal nacheinander geworfen.
Es interessiert, ob die Augenzahl oben liegt oder nicht.
oben liegt oder nicht.
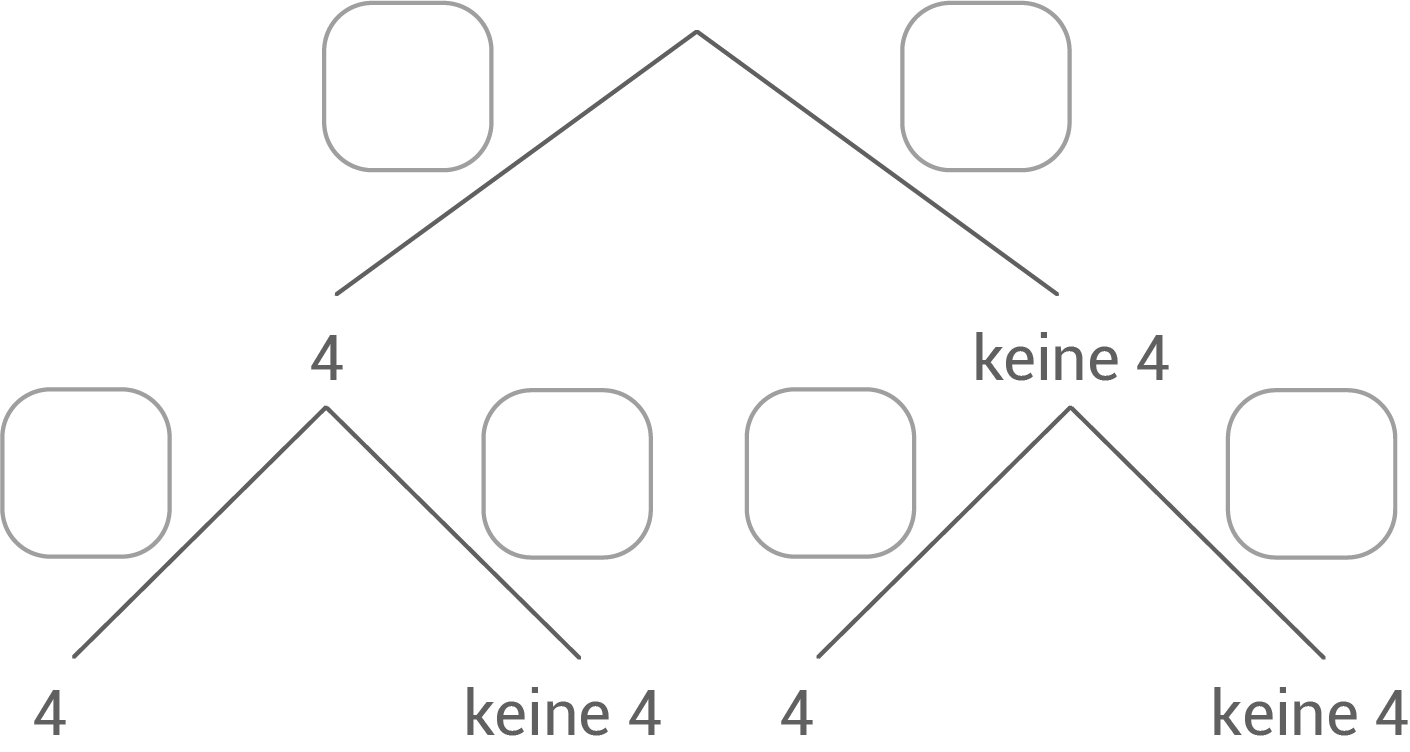 Beschrifte alle Pfade mit ihren Wahrscheinlichkeiten.
Beschrifte alle Pfade mit ihren Wahrscheinlichkeiten.
Es interessiert, ob die Augenzahl

8.
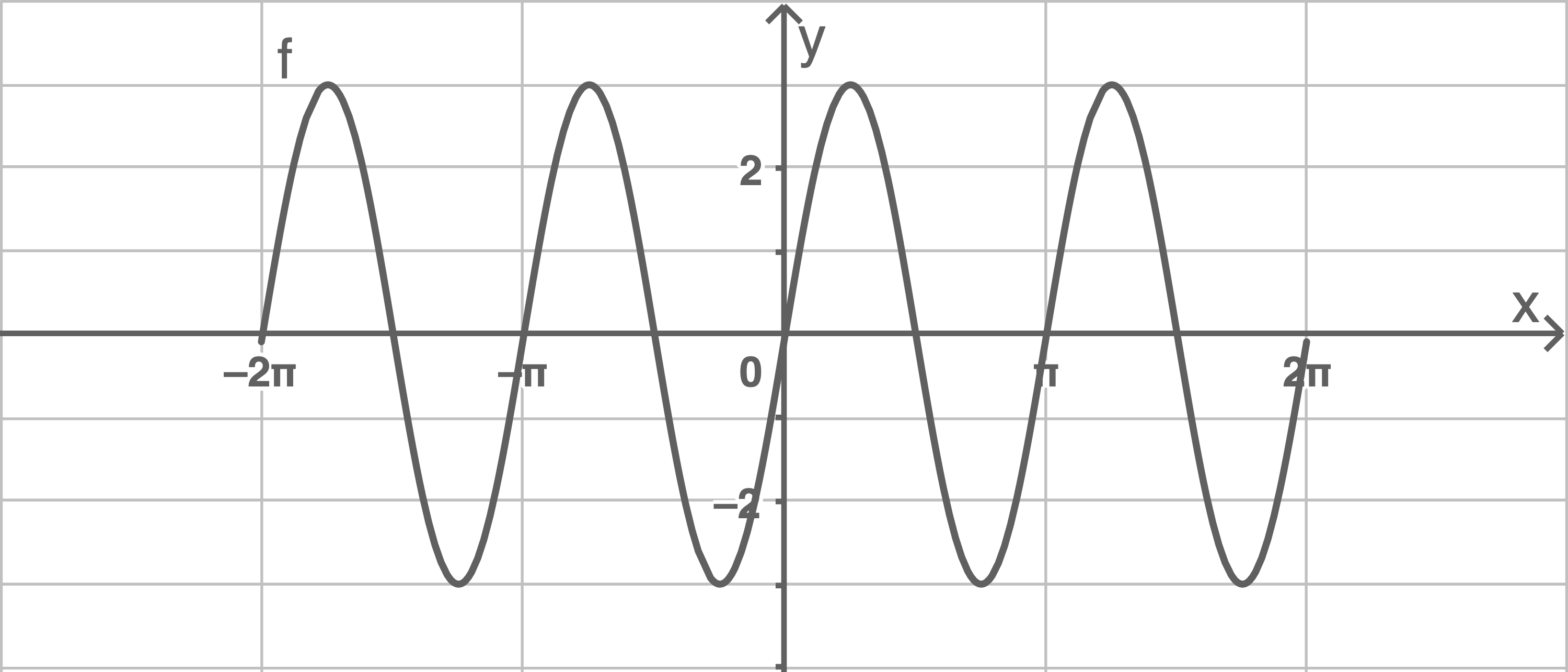
Gib den größten Funktionswert der Funktion  im abgebildeten Intervall an.
im abgebildeten Intervall an.

9.
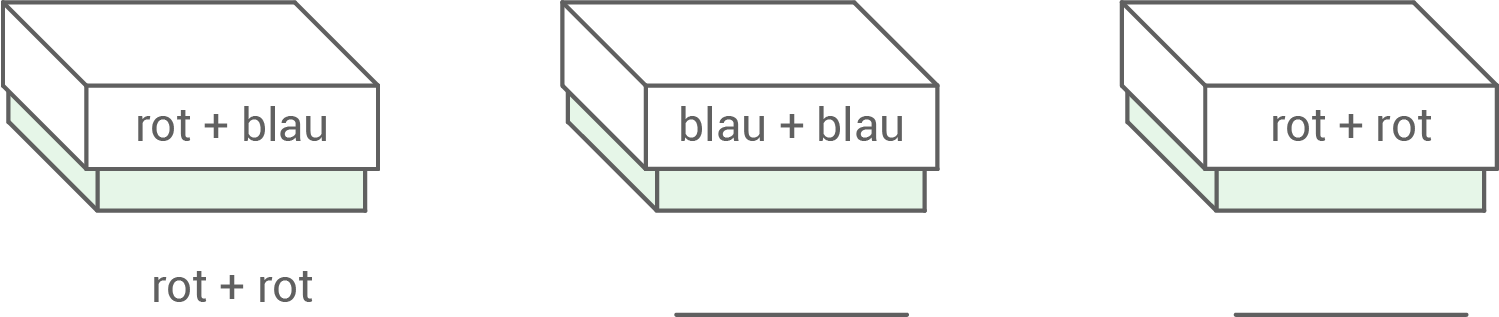
In jeder Schachtel sind genau zwei Kugeln. Bei keiner Schachtel stimmt die Beschriftung mit dem Inhalt überein.
Maren öffnet die Schachtel „rot + blau" und findet in der Schachtel zwei rote Kugeln. Gib an, welche Farben die Kugeln in den beiden anderen Schachteln haben.
Für Teil A erreichbare BE: 12
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
b)
c)
d)
2.
Da an beiden Längenseiten des Tisches Personen sitzen können, saßen an einer Seite des Tisches  Erwachsene.
Der Tisch hat eine Länge von etwa
Erwachsene.
Der Tisch hat eine Länge von etwa  Da 40 knapp die Hälfte von 85 ist, kann abgeschätzt werden, dass jeder am Tisch etwas weniger als einen halben Meter, also etwas weniger als 50 cm, Platz hatte.
Da 40 knapp die Hälfte von 85 ist, kann abgeschätzt werden, dass jeder am Tisch etwas weniger als einen halben Meter, also etwas weniger als 50 cm, Platz hatte.
3.
| wahr | falsch | |
| Die Funktion |
||
| Zwischen den Zahlen |
4.
5.

6.
7.
8.
Der größte Funktionswert der Funktion  ist
ist 
9.
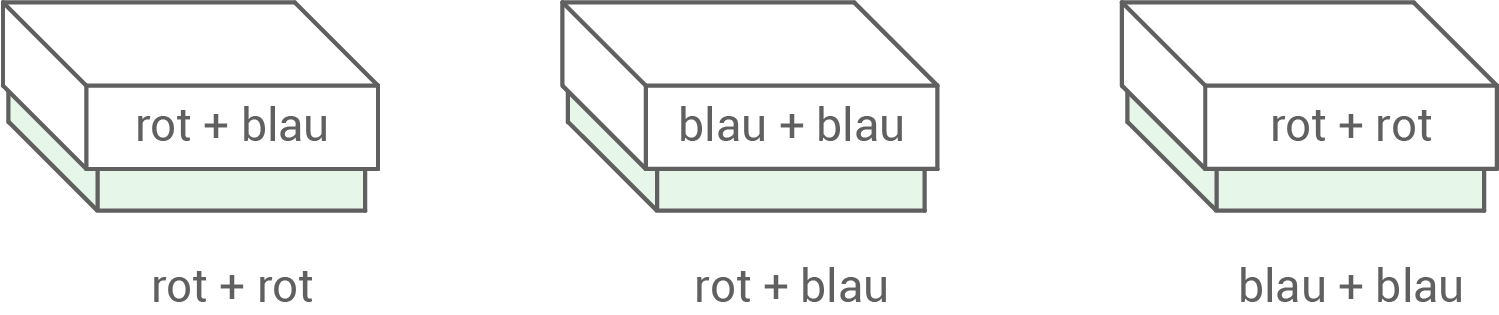
- rot + blau
- blau + blau