Teil B – Wahlaufgaben
Wahlaufgabe 6.1
Gegeben sind drei lineare Funktionen 
 und
und  durch ihre Gleichungen.
durch ihre Gleichungen.
a)
Gib an, welche dieser Funktionen den größten Anstieg hat.
b)
Der Punkt  liegt auf dem Graphen der Funktion
liegt auf dem Graphen der Funktion 
Gib den Funktionswert von Punkt an.
an.
Gib den Funktionswert von Punkt
c)
Die Graphen der Funktionen  und
und  schneiden einander im Punkt
schneiden einander im Punkt 
Berechne die Koordinaten des Punktes
Berechne die Koordinaten des Punktes
d)
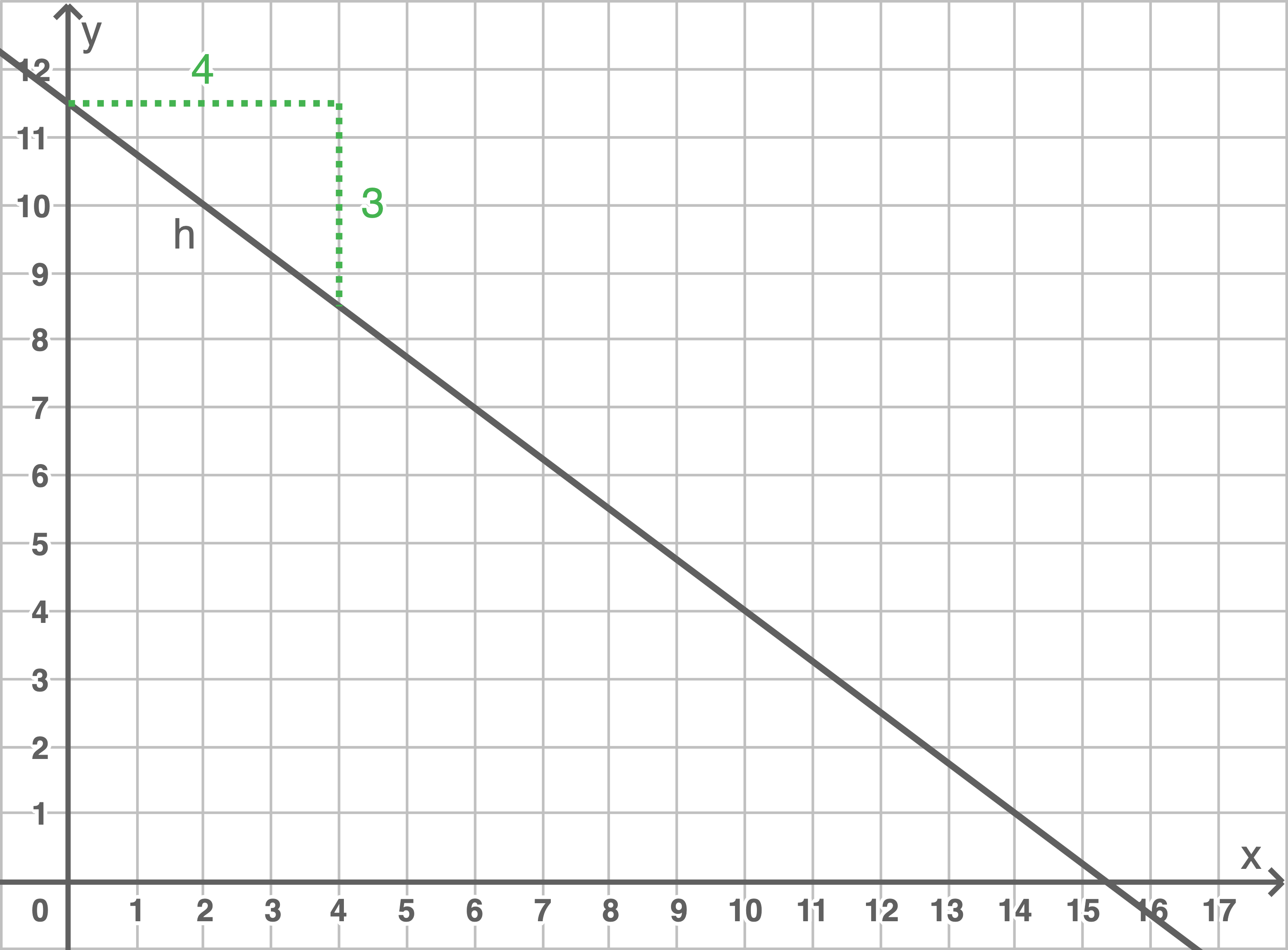
- Zeichne den Graphen der Funktion
in ein Koordinatensystem (Längeneinheit im Koordinatensystem
).
- Der Punkt
liegt auf dem Graphen der Funktion
im ersten Quadranten. Zum Punkt
hat dieser Punkt
einen Abstand von
Berechne die Koordinaten des Punktes
Für Wahlaufgabe 6.1 erreichbare BE: 8
Wahlaufgabe 6.2
Ein Werkstück setzt sich aus einer Halbkugel und einem aufgesetzten Kreiskegel zusammen (siehe Abbildung).
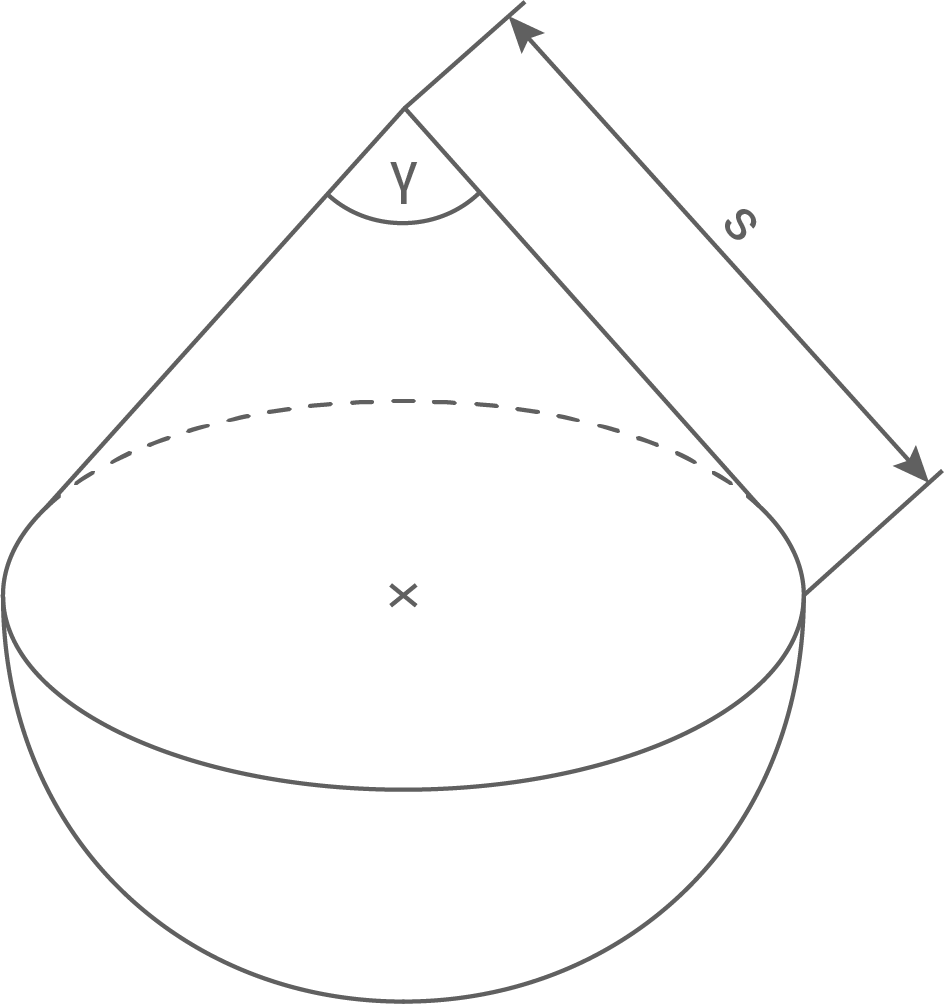 Der Öffnungswinkel
Der Öffnungswinkel  beträgt
beträgt  die Mantellinie
die Mantellinie  hat eine Länge von
hat eine Länge von 

Abbildung (nicht maßstäblich)
a)
Berechne den Radius der Grundfläche des Kreiskegels.
b)
Zeichne ein Zweitafelbild des Werkstückes.
c)
Berechne das Volumen des Werkstückes.
d)
Es werden  dieser Werkstücke aus dem gleichen Material hergestellt. Sie haben zusammen eine Masse von
dieser Werkstücke aus dem gleichen Material hergestellt. Sie haben zusammen eine Masse von 
Gib an, aus welchem der angegebenen Materialien diese Werkstücke bestehen.
| Material | Dichte in |
|---|---|
| Beton | |
| Aluminium | |
| Stahl | |
| Messing |
Für Wahlaufgabe 6.2 erreichbare BE: 8
Wahlaufgabe 6.3
Im Jahr 2016 hatte Artur für sein Office einen Energiebedarf von  Dafür zahlte er
Dafür zahlte er  ohne Grundgebühr an das örtliche Energieunternehmen.
Artur nutzt zur Beleuchtung seines Offices zwölf Glühlampen, auf die
ohne Grundgebühr an das örtliche Energieunternehmen.
Artur nutzt zur Beleuchtung seines Offices zwölf Glühlampen, auf die  des Energiebedarfs des Offices entfallen.
des Energiebedarfs des Offices entfallen.

a)
Gib den Preis für eine Kilowattstunde bei diesem Energieunternehmen an.
b)
Gib an, wie viel Euro Artur 2016 für die Beleuchtung seines Offices bezahlt hat.
c)
Artur möchte die bisherigen  -Watt-Glühlampen durch
-Watt-Glühlampen durch  -Watt-LED-Lampen ersetzen. Er vergleicht für beide Lampenarten die Kosten für die Beleuchtung des Offices bei gleichem Nutzungsverhalten in einem Jahr.
-Watt-LED-Lampen ersetzen. Er vergleicht für beide Lampenarten die Kosten für die Beleuchtung des Offices bei gleichem Nutzungsverhalten in einem Jahr.
- Berechne, wie viel Euro Artur durch den Austausch der zwölf Lampen weniger an das Energieunternehmen pro Jahr bezahlen muss.
- Eine solche LED-Lampe kostet
in der Anschaffung.
Ermittle, nach wie vielen Monaten er die Anschaffungskosten durch den geringeren Energiebedarf eingespart hat.
d)
Entscheide, ob die Aussage im Werbeplakat wahr oder falsch ist.
Begründe deine Entscheidung rechnerisch.
Begründe deine Entscheidung rechnerisch.

Für Wahlaufgabe 6.3 erreichbare BE: 8
Lösung 6.1
a)
Funktion  hat den größten Anstieg.
hat den größten Anstieg.
b)
c)
Gleichsetzungsverfahren anwenden:
![\(\begin{array}[t]{rll}
\dfrac{1}{2}x+4&=&-\dfrac{3}{4}x+11,5 &\quad \scriptsize \mid\;+\dfrac{3}{4}x \\[5pt]
\dfrac{5}{4}x+4&=&11,5 &\quad \scriptsize \mid\;-4 \\[5pt]
\dfrac{5}{4}x&=&7,5 &\quad \scriptsize \mid\;\cdot 4 \\[5pt]
5x&=&30&\quad \scriptsize \mid\;:5 \\[5pt]
x&=&\underline{\underline{ 6}}
\end{array}\)](https://www.schullv.de/resources/formulas/51147a53b445cf99d2f66990e73c0784f9675917fae393158ca98aad5e5f282e_light.svg)
 in Gleichung
in Gleichung  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=&\dfrac{1}{2}x+4 \\[5pt]
y&=&\dfrac{1}{2}\cdot 6+4 \\[5pt]
y&=&\underline{\underline{ 7}}
\end{array}\)](https://www.schullv.de/resources/formulas/899c0f6dedeed1a7894602b0c0a430de4f01973e93a1bab0790ea864b2032c70_light.svg) Der Schnittpunkt hat die Koordinaten
Der Schnittpunkt hat die Koordinaten 
d)
Graphen der Funktion  zeichnen
zeichnen
 Koordinaten des Punktes
Koordinaten des Punktes  berechnen
berechnen
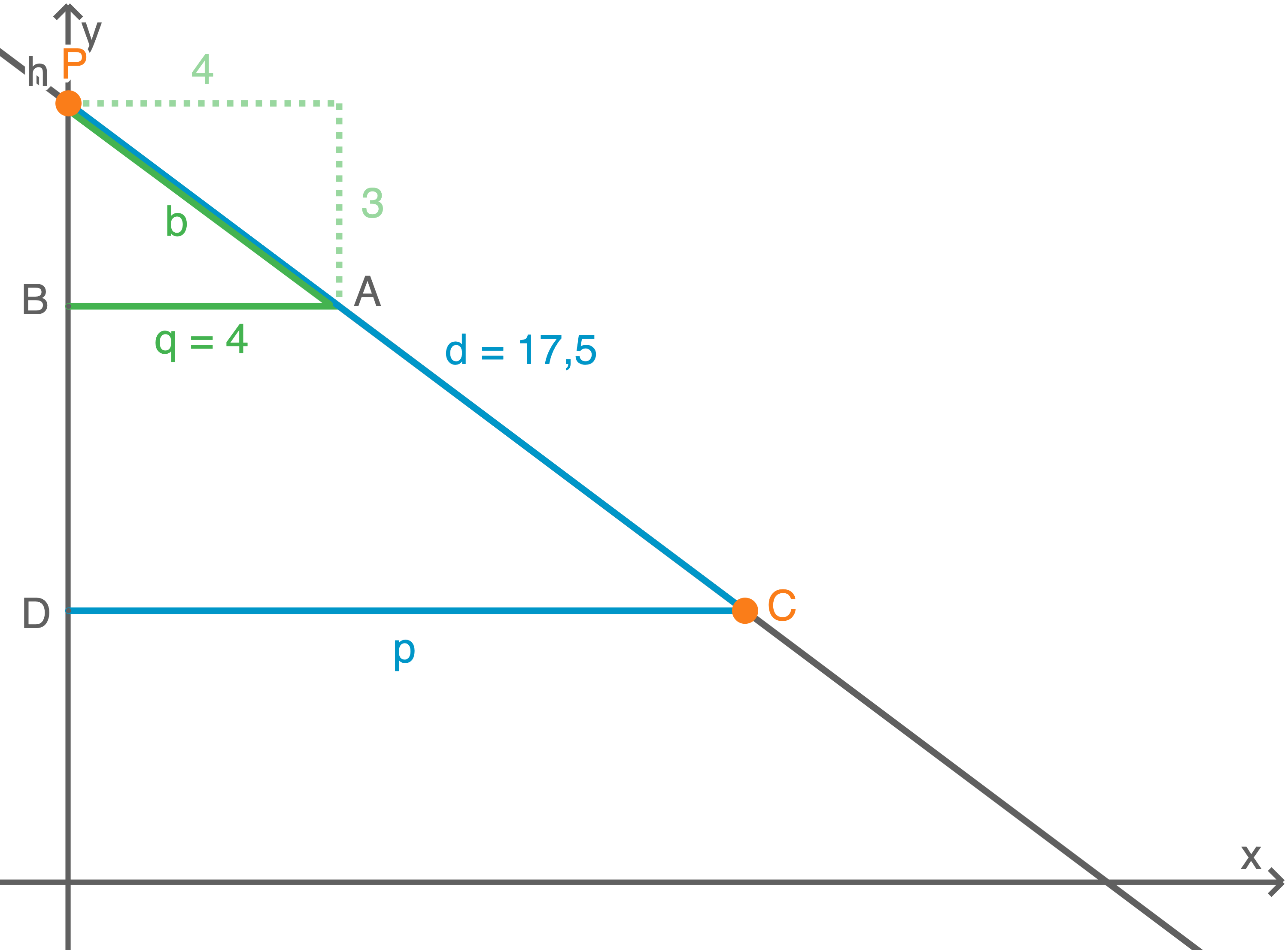 Länge der Hypotenuse
Länge der Hypotenuse  berechnen
Satz des Pythagoras anwenden:
berechnen
Satz des Pythagoras anwenden:
![\(\begin{array}[t]{rll}
b^2&=& 3^2+4^2&\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
b&=& \sqrt{3^2+4^2} \\[5pt]
b&=& \sqrt{25} \\[5pt]
b&=&5
\end{array}\)](https://www.schullv.de/resources/formulas/09223dd9895c08f125a065ef17862de923f5d8af701aebebb577cba990307218_light.svg) Länge der Seite
Länge der Seite  berechnen
Verhältnisgleichung anwenden:
berechnen
Verhältnisgleichung anwenden:
![\(\begin{array}[t]{rll}
\dfrac{p}{d}&=&\dfrac{q}{b} &\quad \scriptsize \mid\;\cdot d \\[5pt]
p&=&\dfrac{q}{b}\cdot d \\[5pt]
p&=&\dfrac{4}{5}\cdot 17,5 \\[5pt]
p&=&14
\end{array}\)](https://www.schullv.de/resources/formulas/25914d5b19c4180fd42220e77a96366eb2b4b58275db89d7a1bc09b32a16ae2d_light.svg) Der berechnete Wert
Der berechnete Wert  entspricht der
entspricht der  -Koordinate des Punktes
-Koordinate des Punktes 
 in Gleichung
in Gleichung  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
y&=&-\dfrac{3}{4}x+11,5 \\[5pt]
y&=&-\dfrac{3}{4}\cdot 14+11,5 \\[5pt]
y&=&1
\end{array}\)](https://www.schullv.de/resources/formulas/a5c7d60f7fe7b9f5f275c9e54f8dcc8ba22c3e4da4cf66fc6be436a877cbbc00_light.svg) Der Punkt
Der Punkt  hat die Koordinaten
hat die Koordinaten 


Lösung 6.2
a)
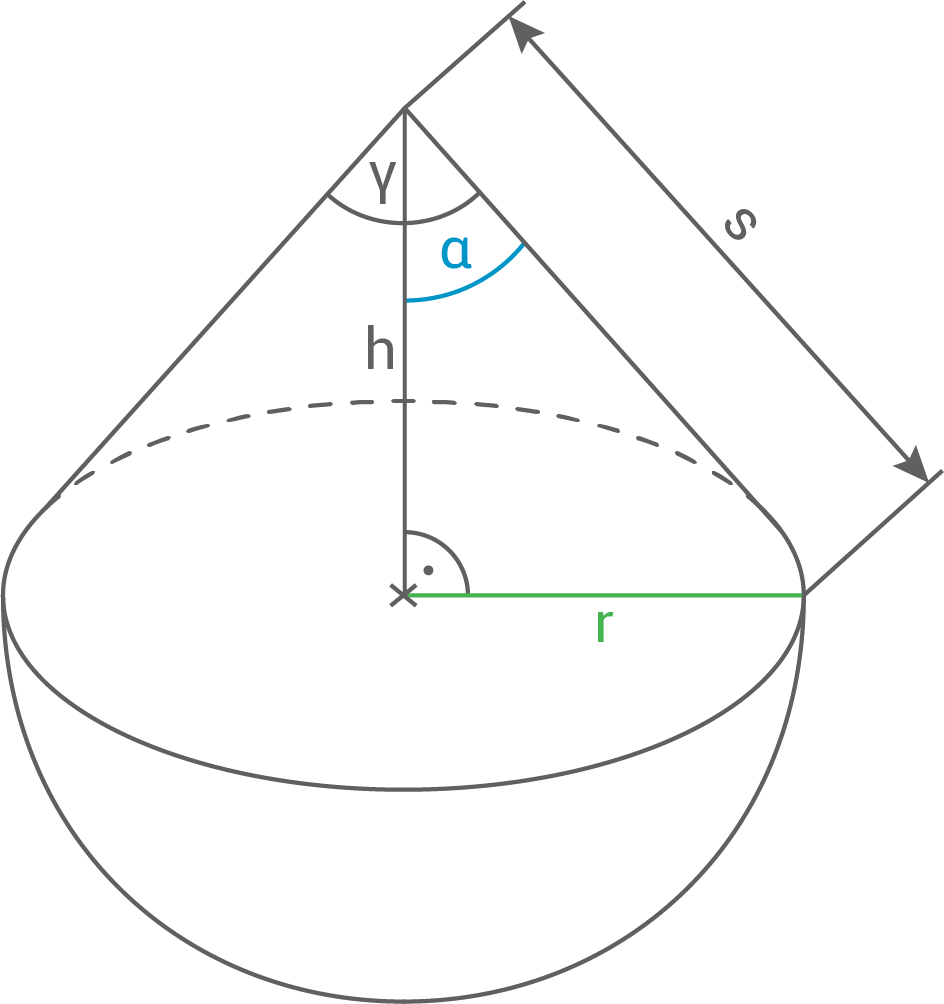
b)
Für das Zweitafelbild wird zunächst die Höhe  des Kreiskegels benötigt:
des Kreiskegels benötigt:
![\(\begin{array}[t]{rll}
h^2+r^2&=& s^2&\quad \scriptsize \mid\;-r^2 \\[5pt]
h^2&=& s^2-r^2&\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
h&=& \sqrt{s^2-r^2} \\[5pt]
h&=& \sqrt{(4,0\,\text{cm})^2-(3,1\,\text{cm})^2} \\[5pt]
h&\approx & 2,5\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/3c79e22f3bebecfe3b21c6991c7cf4ee7c5812354e5f6fd4724ed61071a49ed1_light.svg) Mit dieser Angabe kann das Zweitafelbild gezeichnet werden:
Mit dieser Angabe kann das Zweitafelbild gezeichnet werden:
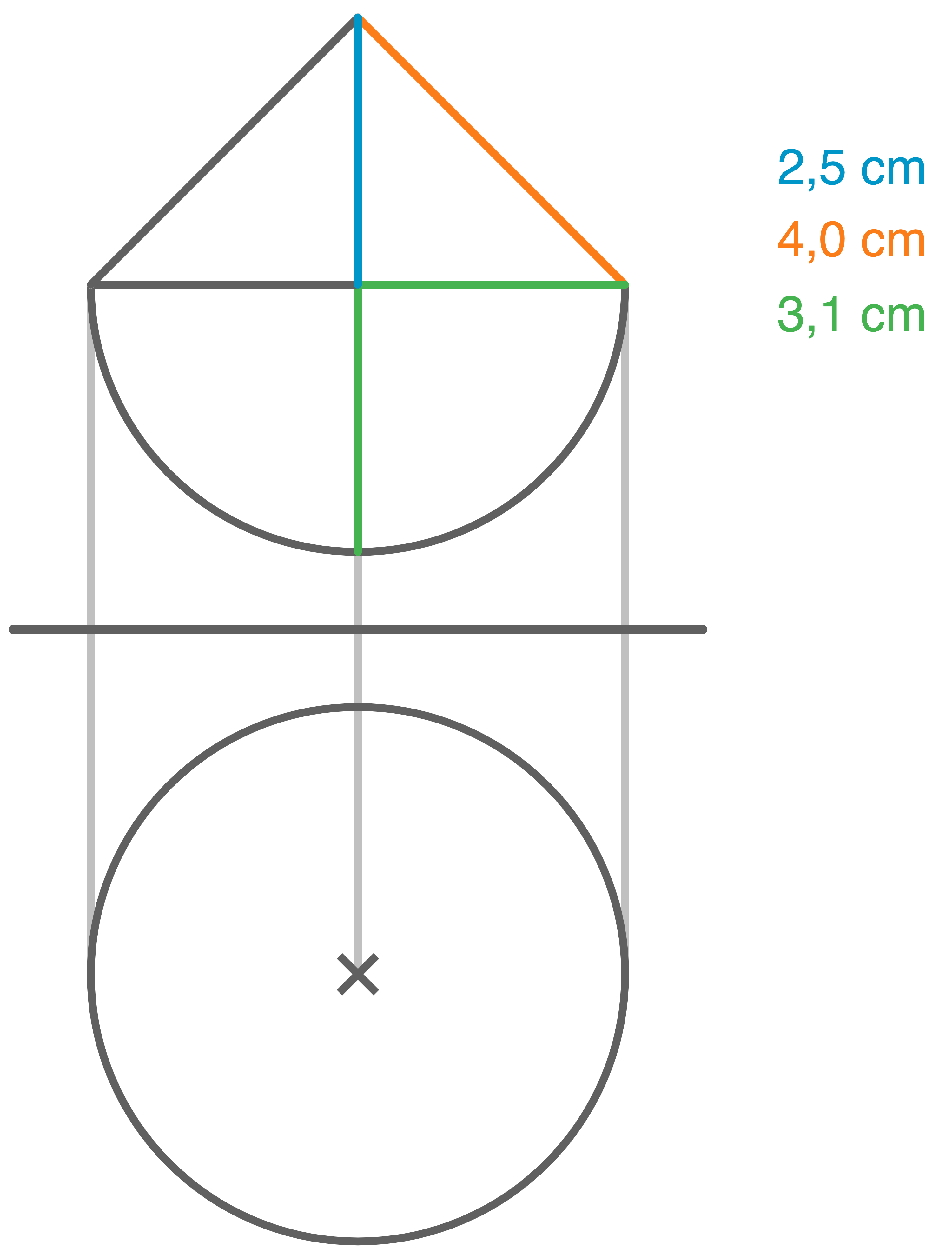

c)
Volumen des Kreiskegels berechnen
![\(\begin{array}[t]{rll}
V_K&=&\dfrac{1}{3}\cdot \pi \cdot r^2\cdot h \\[5pt]
V_K&=&\dfrac{1}{3}\cdot \pi \cdot (3,1\,\text{cm})^2\cdot 2,5\,\text{cm} \\[5pt]
V_K&\approx&25,2\,\text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/63e771bd117ac78e24fbdbc676eda5504022dfedad28170253c1963478163f6c_light.svg) Volumen der Halbkugel berechnen
Volumen der Halbkugel berechnen
![\(\begin{array}[t]{rll}
V_H&=&\dfrac{1}{2}\cdot \dfrac{4}{3}\cdot \pi\cdot r^3 \\[5pt]
V_H&=&\dfrac{1}{2}\cdot \dfrac{4}{3}\cdot \pi\cdot (3,1\,\text{cm})^3 \\[5pt]
V_H&\approx&62,4\,\text{cm}^3 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4f8807cea9cd3a675394b1e0755c217e569b56dd39d579a2f5e49d4a1c3a2ebc_light.svg) Volumen des Werkstückes berechnen
Volumen des Werkstückes berechnen
![\(\begin{array}[t]{rll}
V_W&=& V_K+V_H \\[5pt]
V_W&=& 25,2\,\text{cm}^3+62,4\,\text{cm}^3 \\[5pt]
V_W&=& \underline{\underline{ 87,6\,\text{cm}^3}}
\end{array}\)](https://www.schullv.de/resources/formulas/76bc3c6825a168d9ab183e6b05a5e84c5c1b9381901eed1d6d21e34884d3793b_light.svg)
d)
Masse eines Werkstückes berechnen
 Dichte des Materials berechnen
Dichte des Materials berechnen
 Da laut Tabelle Aluminium eine Dichte von
Da laut Tabelle Aluminium eine Dichte von  hat, muss das Werkstück aus Aluminium bestehen.
hat, muss das Werkstück aus Aluminium bestehen.
Lösung 6.3
a)
b)
c)
Wie viel Euro muss Artur durch den Austausch weniger an das Energieunternehmen pro Jahr bezahlen?
Die Kosten für die  -Watt-LED-Lampen können über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.
Beispielhafter Lösungsweg über den Dreisatz
-Watt-LED-Lampen können über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.
Beispielhafter Lösungsweg über den Dreisatz




![\(\begin{array}{rcl}
60\,\text{W}& \mathrel{\widehat{=}}& 76,87\,€\\[5pt]
1\,\text{W}& \mathrel{\widehat{=}}& \dfrac{76,87}{60}\,€\\[5pt]
11\,\text{W}& \mathrel{\widehat{=}}& \dfrac{76,87}{60}\cdot 11\,€\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/550a85bd675577d26b926e5d49afbd5a0fd6a5060129a119714e6b6d9912474c_light.svg)




 Daraus folgt:
Daraus folgt:
 Durch den Austausch muss Artus
Durch den Austausch muss Artus  pro Jahr weniger an das Energieunternehmen bezahlen.
Nach wie vielen Monaten hat Artur die Anschaffungskosten durch den geringeren Energiebedarf eingespart?
Die Anschaffungskosten der LED-Lampen betragen
pro Jahr weniger an das Energieunternehmen bezahlen.
Nach wie vielen Monaten hat Artur die Anschaffungskosten durch den geringeren Energiebedarf eingespart?
Die Anschaffungskosten der LED-Lampen betragen  Die Einsparung pro Monat beträgt
Die Einsparung pro Monat beträgt  Daraus folgt:
Daraus folgt:
 Nach 16 Monaten hat Artur die Anschaffungskosten durch den geringeren Energiebedarf eingespart.
Nach 16 Monaten hat Artur die Anschaffungskosten durch den geringeren Energiebedarf eingespart.
d)
Die tatsächliche Einsparung beträgt  Die Einsparung laut Werbeplakat kann über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.
Beispielhafter Lösungsweg über den Dreisatz
Die Einsparung laut Werbeplakat kann über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.
Beispielhafter Lösungsweg über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 60\,\text{W}\\[5pt]
1\,\% & \mathrel{\widehat{=}}& \dfrac{60}{100}\,\text{W}\\[5pt]
80\,\% & \mathrel{\widehat{=}}& \dfrac{60}{100}\cdot 80\,\text{W}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b60bb2a743b242b06f7daac507b2ceae953afb948fc79404d0a20e5c7e5f05a2_light.svg)




 Mit
Mit  Watt werden sogar mehr als
Watt werden sogar mehr als  Watt eingespart. Die Werbeaussage ist somit wahr.
Watt eingespart. Die Werbeaussage ist somit wahr.