Teil B – Pflichtaufgaben

Aufgabe 1

Der Flughafen Leipzig-Halle hat in den letzten Jahren seine Auslastung kontinuierlich gesteigert.

Die Tabelle zeigt die Entwicklung der Anzahl der Fluggäste.

Jahr	Anzahl der Fluggäste
2013	$2 \, 240 \, 860$
2015	$2 \, 321 \, 975$
2017	$2 \, 365 \, 141$

Berechne, auf wie viel Prozent die Anzahl der Fluggäste im Jahr 2017 gegenüber dem Jahr 2013 gestiegen ist.

Die Masse der transportierten Luftfracht im Jahr 2013 betrug $887\,100$ Tonnen.
Der Transport von Luftfracht ist im Jahr 2017 um $28,33\,\%$ gegenüber 2013 gestiegen.

Berechne die Masse der Luftfracht im Jahr 2017.

Im Jahr 2013 betrug die Anzahl der Flüge $61\,668.$ Das sind $88,33\,\%$ der Flüge des Jahres 2017.

Berechne die Anzahl der Flüge im Jahr 2017.

Für Aufgabe 1 erreichbare BE: 6

Aufgabe 2

Gegeben ist ein Rhombus $ABCD$ durch die Diagonalen $\overline{AC}=e=6,0\,\text{cm}$ und $\overline{BD}=f=8,0\,\text{cm}.$

Berechne den Flächeninhalt des Rhombus $ABCD.$

Konstruiere den Rhombus $ABCD.$

Der Verschiebungspfeil $\overrightarrow{AC}$ gibt die Richtung und die Länge einer Verschiebung an.

Zeichne den Bildpunkt $C_1$ des Punktes $C$ bei der Verschiebung $\overrightarrow{AC}$ .
Gib die Vierecksart der Figur $ABC_1D$ an.
Begründe, dass der Flächeninhalt $ABC_1D$ genau doppelt so groß ist wie der Flächeninhalt des Rhombus $ABCD.$

Für Aufgabe 2 erreichbare BE: 7

Aufgabe 3

Gegeben ist die Funktion $f$ durch die Gleichung $y=f(x)=x^{-1}\,(x\neq 0)$ .

Übernimm die Wertetabelle und vervollständige diese für die Funktion $f$ .

$\color{#ffffff}{x}$	$-4$	$-2$	$-1$	$-0,5$	$\dfrac{1}{4}$	$2,5$
$\color{#ffffff}{y}$							$\dfrac{1}{4}$

Zeichne den Graphen der Funktion $f$ in ein Koordinatensystem mindestens im Intervall $-4\leq x\leq 4.$

Eine weitere Funktion $g$ ist durch die Gleichung $y=g(x)=2x-1$ gegeben.

Zeichne den Graphen der Funktion $g$ in dasselbe Koordinatensystem.
Die Graphen der Funktion $f$ und $g$ haben zwei Schnittpunkte.
Gib die Koordinaten dieser beiden Schnittpunkte an.

Für Aufgabe 3 erreichbare BE: 6

Aufgabe 4

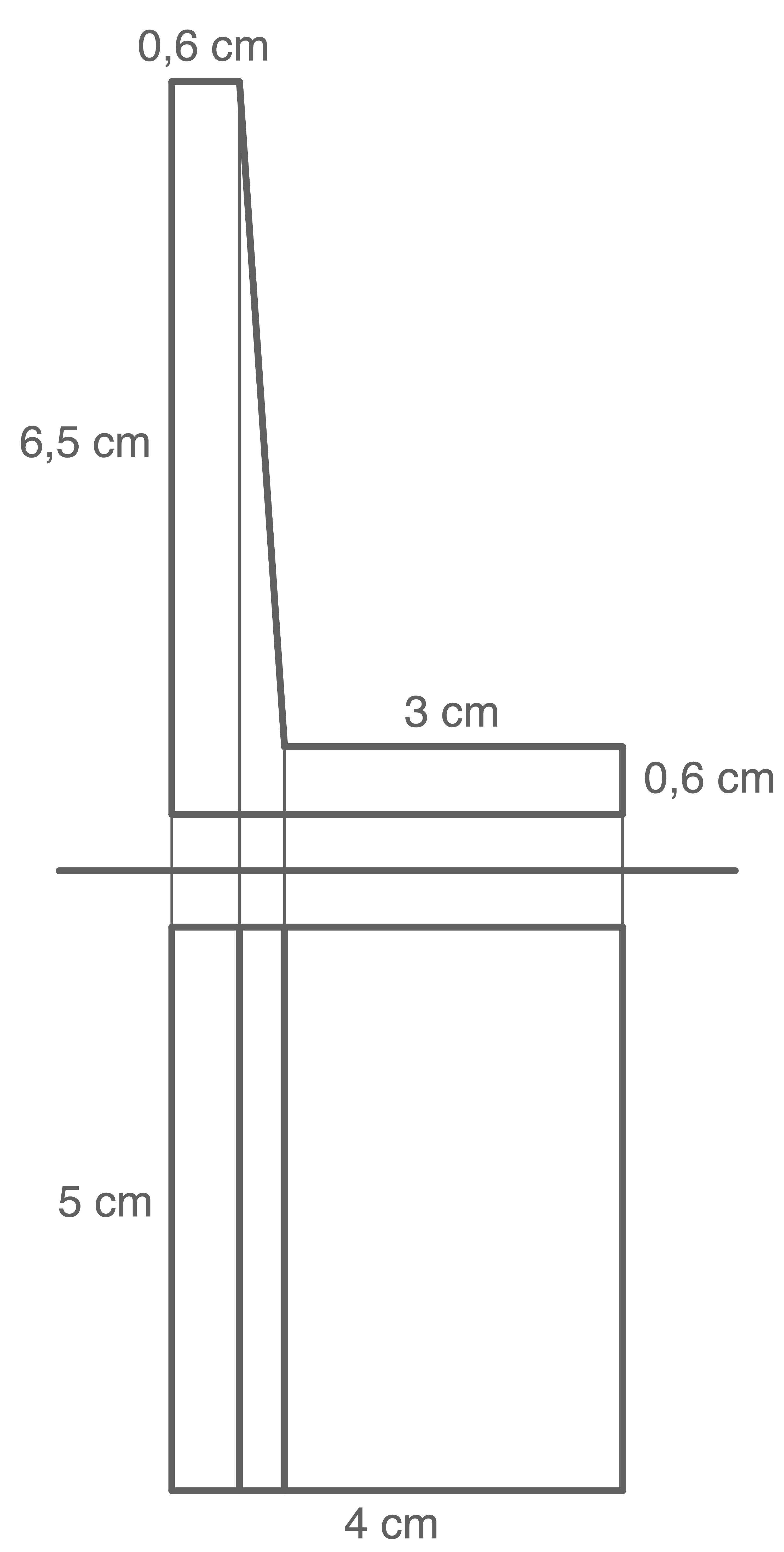
Eine Firma fertigt prismenförmige Stützen für den Straßenbau an (siehe Abbildung).

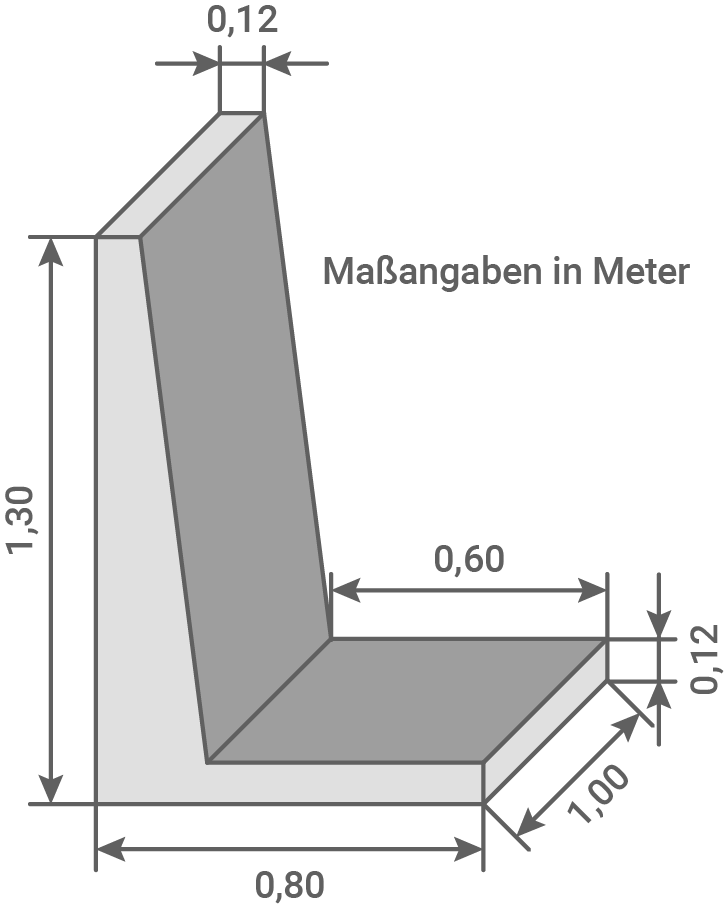
Abbildung (nicht maßstäblich)

Zeichne ein senkrechtes Zweitafelbild einer Stütze in einem geeigneten Maßstab.

Berechne das Volumen einer Stütze.

Die Stützen bestehen aus Beton mit einer Dichte von $2,60\,\dfrac{\text{t}}{\text{m}^3}$ .
Gib die Masse einer Stütze an.

Für Aufgabe 4 erreichbare BE: 6

Pflichtaufgabe 5

Ben und Carmen möchten aus Draht achsensymmetrische Figuren in Form von Fischen herstellen. Sie haben dafür eine Vorlage, mit der sie unterschiedlich große Figuren basteln können (siehe Abbildung).

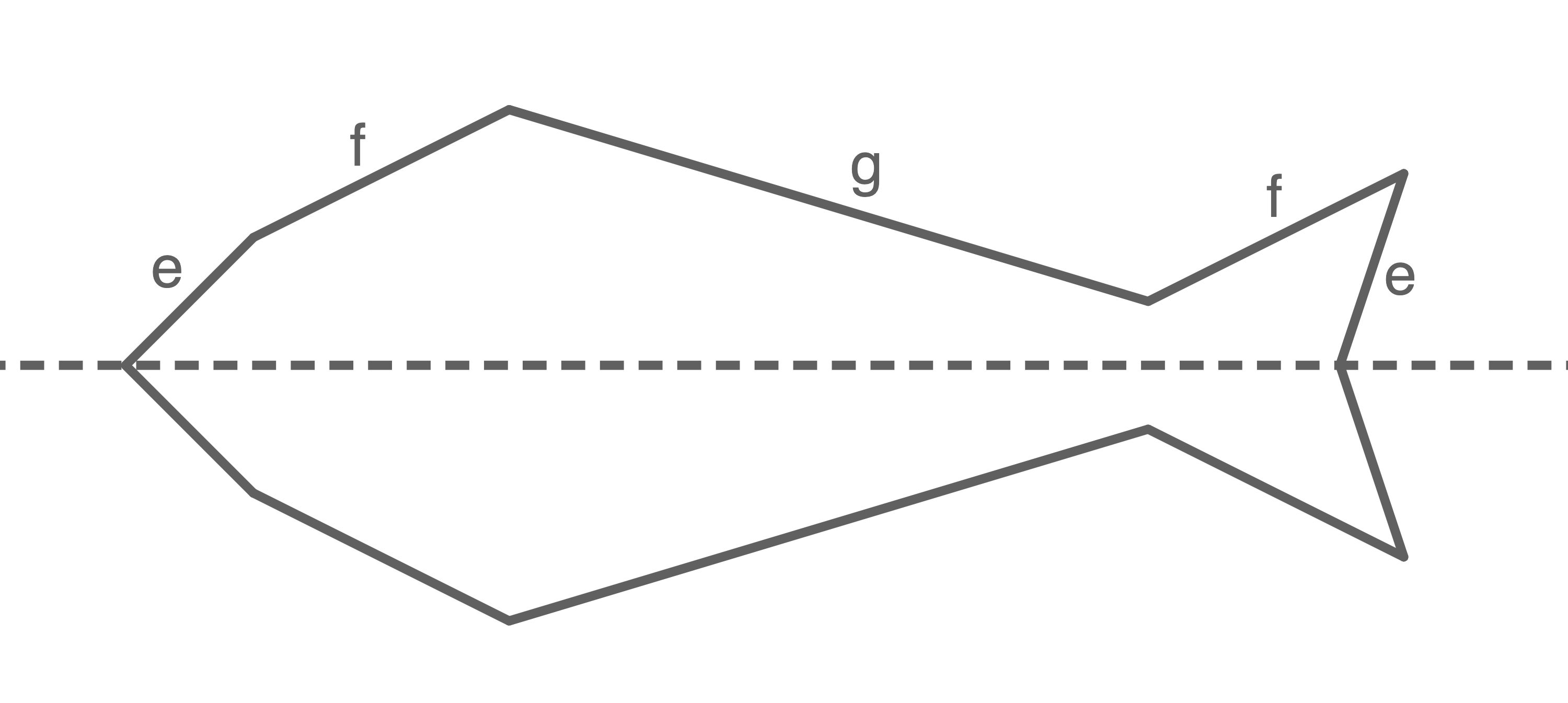
Abbildung (nicht maßstäblich)

Stelle einen Term für den Umfang der Figur mit den angegebenen Variablen auf.

In der Vorlage ist die Teilstrecke $f$ doppelt so lang wie die Teilstrecke $e$ und die Teilstrecke $g$ dreimal so lang wie die Teilstrecke $e.$

Ben wählt für $e$ eine Länge von $20\,\text{mm}.$
Berechne, wie viel Zentimeter Draht er für die Herstellung einer Figur mindestens benötigt.
Carmen hat für eine Figur genau $1,08\,\text{m}$ Draht verwendet.
Ermittle, wie lang sie die Teilstrecken $e,$ $f$ und $g$ gewählt hat.

Für Aufgabe 5 erreichbare BE: 5

Lösung 1

Lösungsweg über den Dreisatz

Dreisatz anzeigen

$2\,365\,141 \mathrel{\widehat{=}} \underline{\underline{ 105,55\,\%}}$

Lösungsweg über die Verhältnisgleichung

$\begin{array}[t]{rll} \dfrac{x}{ 2\,365\,141}&=&\dfrac{100\,\%}{2\,240\,860} &\scriptsize \mid\; \cdot 2\,365\,141\\[5pt] x&=&\dfrac{100\,\%}{2\,240\,860}\cdot 2\,365\,141 \\[5pt] x&\approx& \underline{\underline{ 105,55\,\%}} \end{array}$

Lösungsweg über die Prozentformel

$\begin{array}[t]{rll} p\,\%&=&\dfrac{W\cdot 100}{G} \,\%\\[5pt] p\,\%&=&\dfrac{2\,365\,141\cdot 100}{2\,240\,860} \,\% \\[5pt] p\,\%&\approx&\underline{\underline{ 105,55\,\%}} \end{array}$

Lösungsweg über den Dezimalbruch

$\dfrac{2\,365\,141}{2\,240\,860}\approx1,0555=\underline{\underline{ 105,55\,\%}}$

Die Anzahl der Fluggäste ist im Jahr 2017 gegenüber dem Jahr 2013 auf $105,55\,\%$ gestiegen.

Auch hier kann die Masse der Luftfracht über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.

Beispielhafter Lösungsweg über die Prozentformel

$\begin{array}[t]{rll} W&=&\dfrac{G\cdot p}{100} \\[5pt] W&=&\dfrac{887\,100\,\text{t}\cdot 128,33}{100} \\[5pt] W&\approx&\underline{\underline{ 1\,138\,415\,\text{t}}} \end{array}$

Die Masse der Luftfracht im Jahr 2017 betrug $1\,138\,415\,\text{t}.$

Die Anzahl der Flüge kann ebenfalls über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.

Beispielhafter Lösungsweg über die Prozentformel

$\begin{array}[t]{rll} G&=&\dfrac{W\cdot 100}{p} \\[5pt] G&=&\dfrac{61\,668\cdot 100}{88,33} \\[5pt] G&\approx&\underline{\underline{ 69\,815}} \end{array}$

Im Jahr 2017 betrug die Anzahl der Flüge $69\,815.$

Lösung 2

Skizze zur Veranschaulichung:

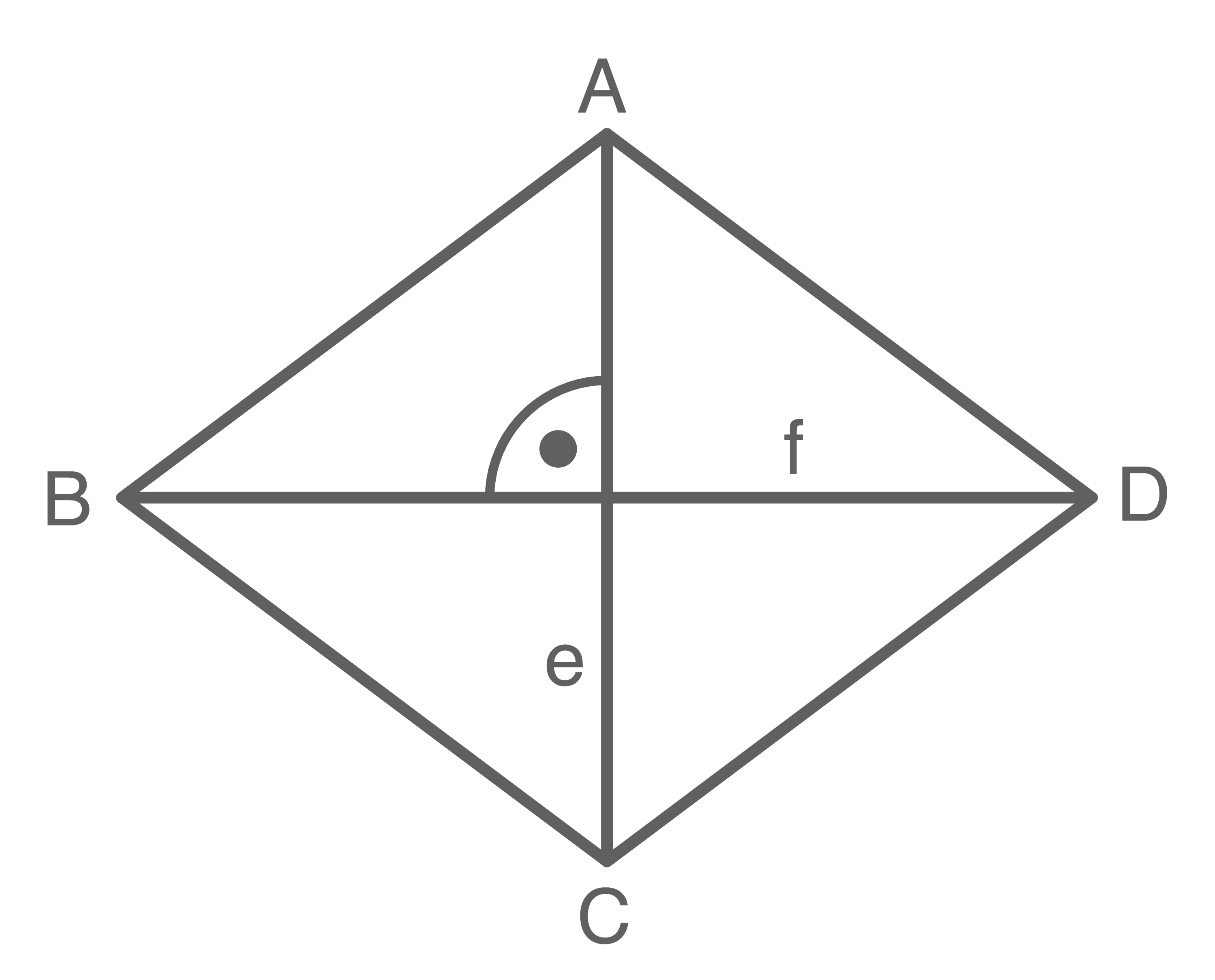
$\begin{array}[t]{rll} A_{ABCD}&=&\dfrac{1}{2}\cdot e\cdot f \\[5pt] A_{ABCD}&=&\dfrac{1}{2}\cdot 6,0\,\text{cm}\cdot 8,0\,\text{cm} \\[5pt] A_{ABCD}&=&\underline{\underline{ 24,0\,\text{cm}^2}} \end{array}$

Konstruktionsschritte:

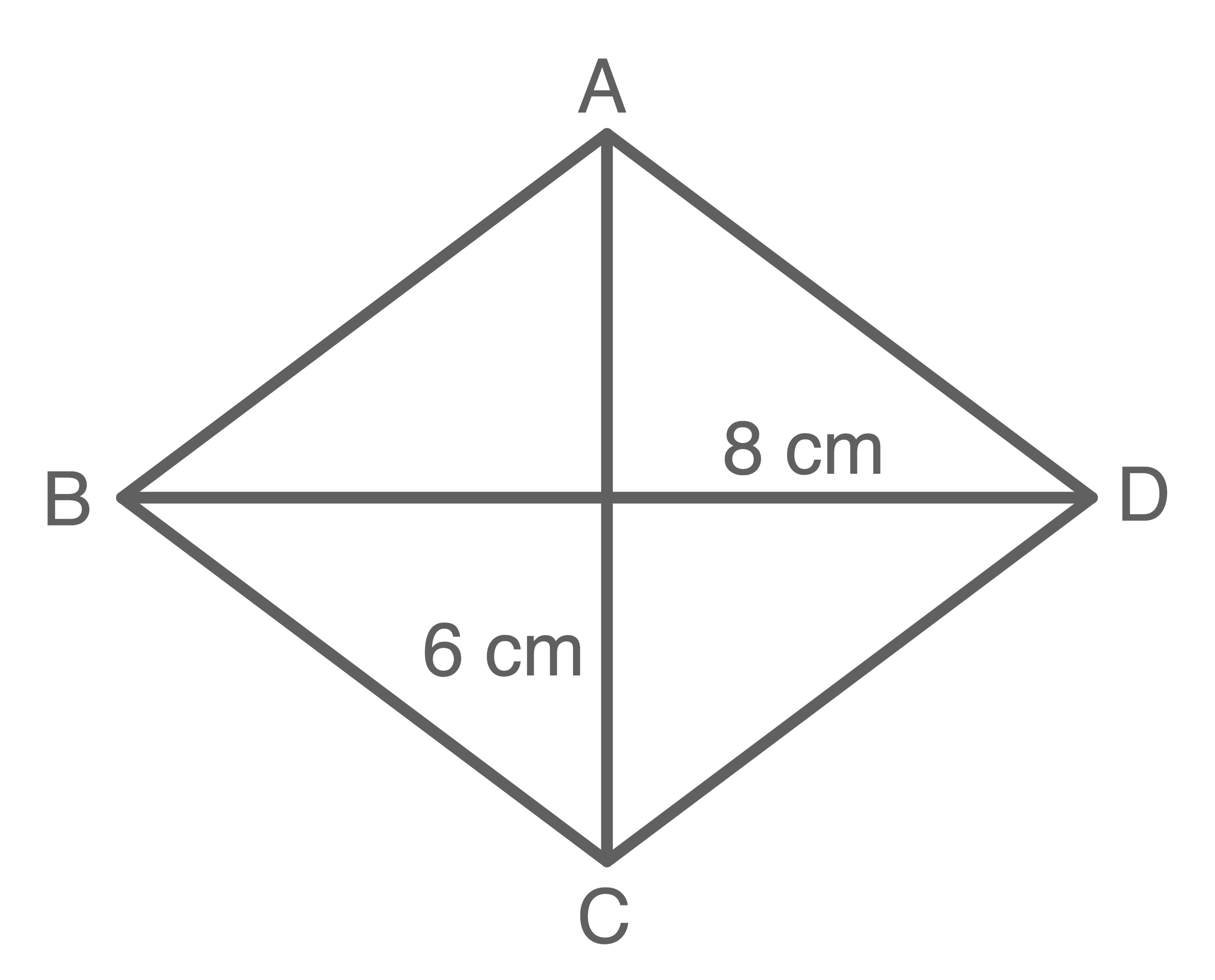
Strecke $\overline{BD}=8,0\,\text{cm}$ zeichnen.
Mittelsenkrechte zu $\overline{BD}$ mit der Länge $6,0\,\text{cm}$ zeichnen. Es entsteht die Strecke $\overline{AC}.$
Punkte verbinden.

Bildpunkt $\boldsymbol{C_1}$ bei der Verschiebung zeichnen

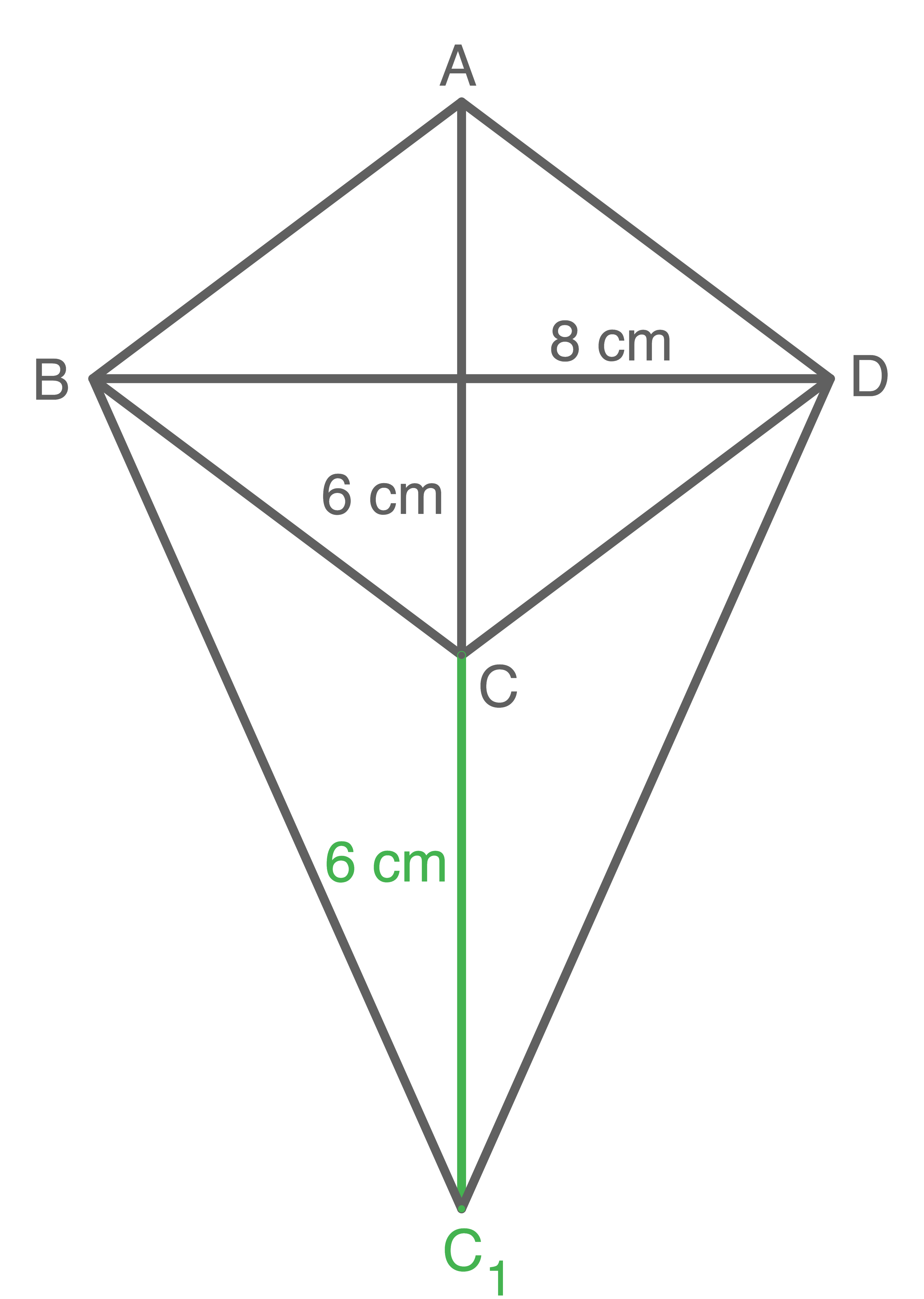Vierecksart angeben

Drachenviereck

Begründen, dass der Flächeninhalt $\boldsymbol{ABC_1D}$ genau doppelt so groß ist wie der Flächeninhalt des Rhombus $\boldsymbol{ABCD}$

$\begin{array}[t]{rll} A_{ABC_1D}&=&\dfrac{1}{2}\cdot 12\,\text{cm}\cdot 8\,\text{cm} \\[5pt] A_{ABC_1D}&=&\underline{\underline{ 48\,\text{cm}^2}} \end{array}$

Daraus folgt: $A_{ABC_1D}=2\cdot A_{ABCD}$

Mit $48\,\text{cm}^2$ ist der Flächeninhalt der Figur $ABC_1D$ genau doppelt so groß wie der Flächeninhalt der Figur $ABCD.$

Lösung 3

Wertetabelle übernehmen und vervollständigen

Es gilt: $x^{-1}=\dfrac{1}{x}$

Somit ordnet die Funktion $f$ jeder Zahl $x$ ihren Kehrwert zu.

$\color{#ffffff}{x}$	$-4$	$-2$	$-1$	$-0,5$	$\dfrac{1}{4}$	$2,5$	$4$
$\color{#ffffff}{y}$	$-0,25$	$-0,5$	$-1$	$-2$	$4$	$0,4$	$\dfrac{1}{4}$

Graphen der Funktion zeichnen

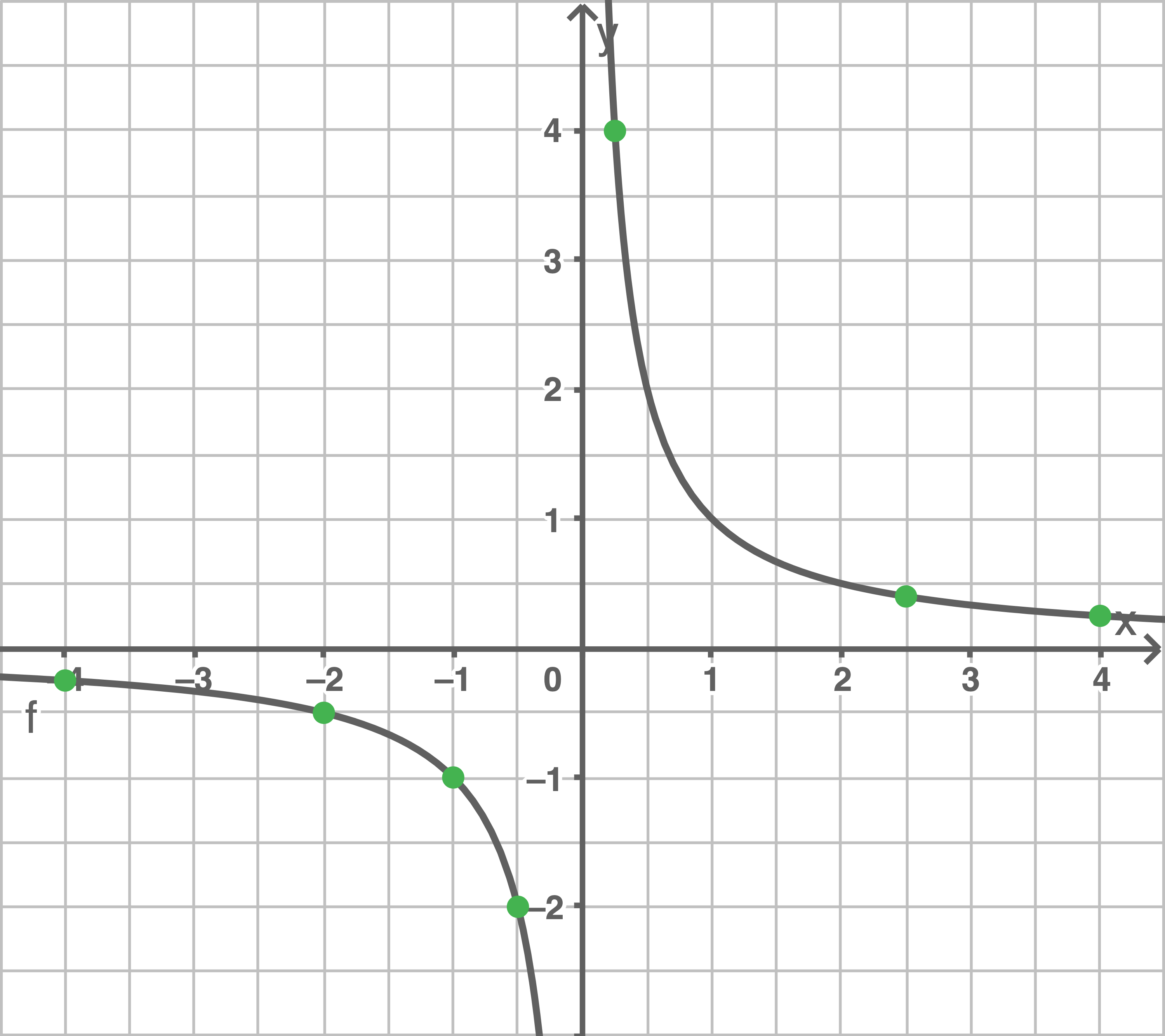
Graphen der Funktion $\boldsymbol{g}$ in dasselbe Koordinatensystem zeichnen

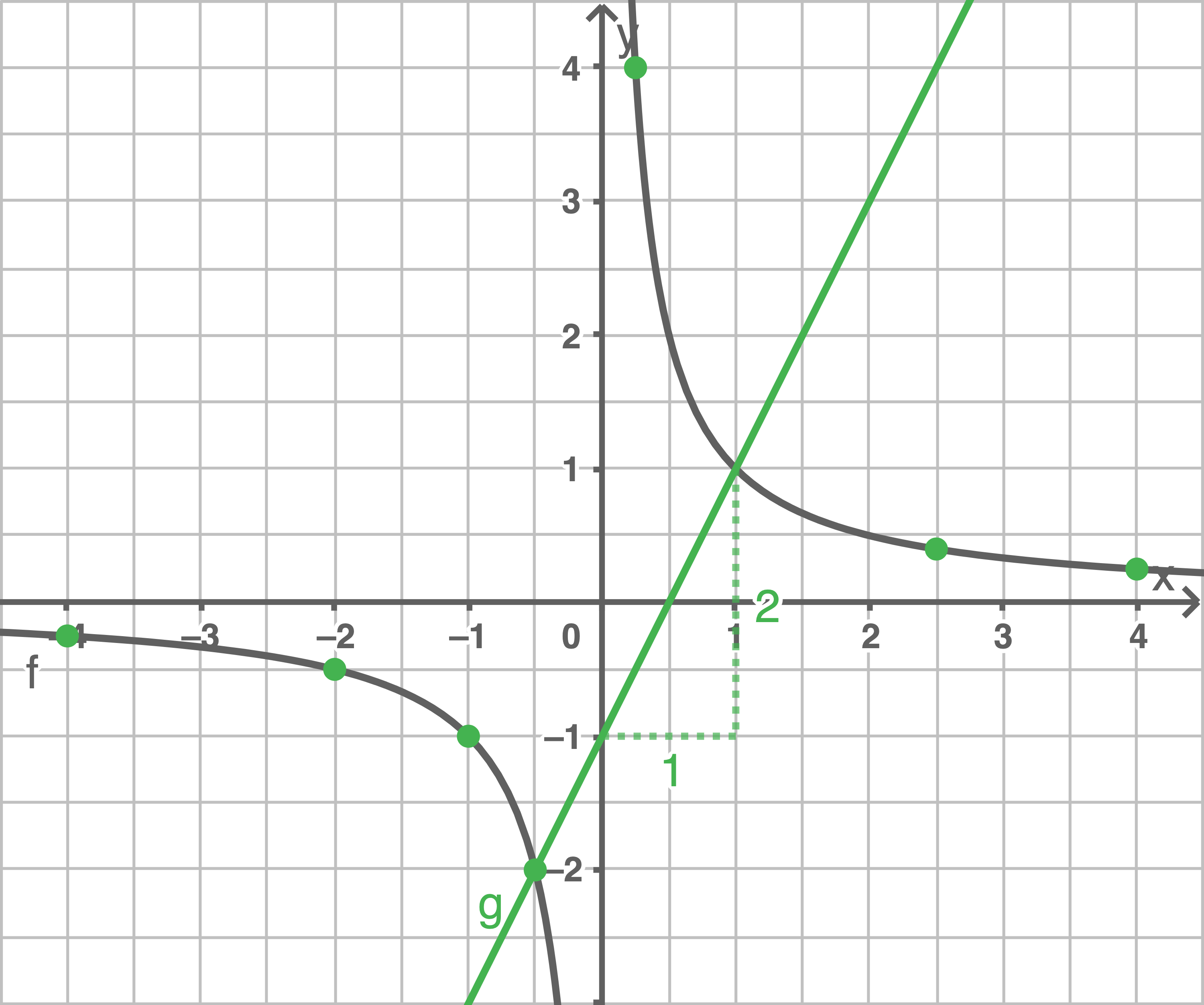Koordinaten der beiden Schnittpunkte angeben

$\underline{\underline{ S_1(-0,5\mid -2)}}$

$\underline{\underline{ S_2(1\mid 1)}}$

Lösung 4

Gewählter Maßstab: 1:20

Originallänge	Bildlänge im Maßstab 1:20
$1,30\,\text{m}=130\,\text{cm}$	$130\,\text{cm}:20=6,5\,\text{cm}$
$1,00\,\text{m}=100\,\text{cm}$	$100\,\text{cm}:20=5\,\text{cm}$
$0,80\,\text{m}=80\,\text{cm}$	$80\,\text{cm}:20=4\,\text{cm}$
$0,60\,\text{m}=60\,\text{cm}$	$60\,\text{cm}:20=3\,\text{cm}$
$0,12\,\text{m}=12\,\text{cm}$	$12\,\text{cm}:20=0,6\,\text{cm}$

Mit diesen Angaben kann das Zweitafelbild gezeichnet werden:

Um das Volumen zu berechnen, wird die Grundfläche in ein Rechteck und ein Trapez zerlegt:

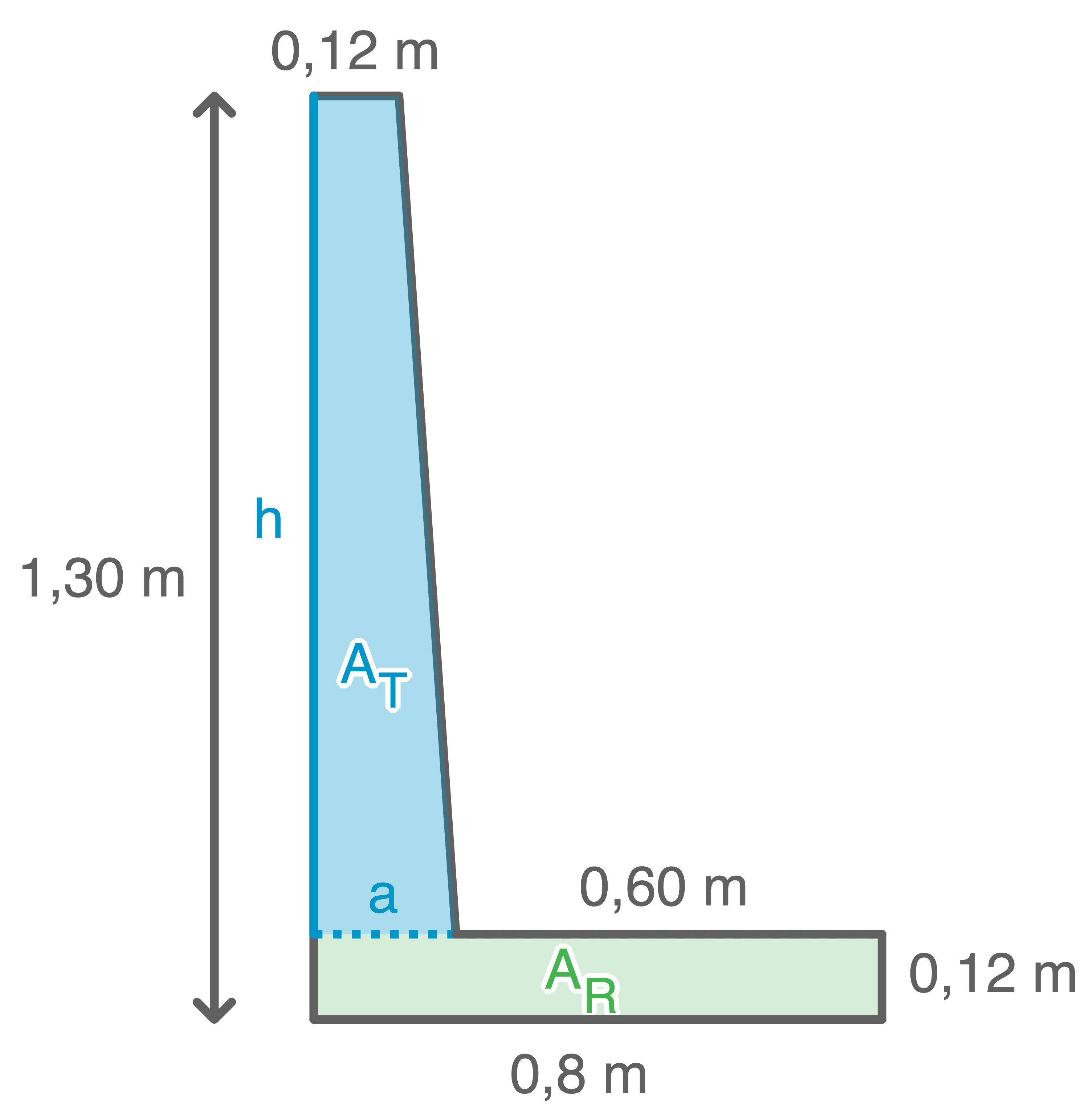Flächeninhalt des Rechtecks berechnen

$\begin{array}[t]{rll} A_R&=&0,80\,\text{m}\cdot 0,12\,\text{m}\\[5pt] A_R&=&0,096\,\text{m}^2 \end{array}$

Flächeninhalt des Trapezes berechnen

Für die Länge von $a$ gilt: $a=0,80\,\text{m}-0,60\,\text{m}=0,20\,\text{m}$

Für die Höhe $h$ gilt: $h=1,30\,\text{m}-0,12\,\text{m}=1,18\,\text{m}$

Damit folgt:

$\begin{array}[t]{rll} A_T&=&\dfrac{a+c}{2}\cdot h \\[5pt] A_T&=&\dfrac{0,20\,\text{m}+0,12\,\text{m}}{2}\cdot 1,18\,\text{m} \\[5pt] A_T&=&0,1888\,\text{m}^2 \\[5pt] \end{array}$

Grundflächeninhalt berechnen

$\begin{array}[t]{rll} A_G&=&A_R+A_T \\[5pt] A_G&=&0,096\,\text{m}^2+0,1888\,\text{m}^2 \\[5pt] A_G&=&0,2848\,\text{m}^2 \\[5pt] \end{array}$

Volumen berechnen

$\begin{array}[t]{rll} V&=&A_G\cdot h \\[5pt] V&=&0,2848\,\text{m}^2\cdot 1,00\,\text{m} \\[5pt] V&=&\underline{\underline{ 0,2848\,\text{m}^3 }} \end{array}$

Das Volumen einer Stütze beträgt $0,2848\,\text{m}^3.$

$\begin{array}[t]{rll} \rho&=& \dfrac{m}{V}&\quad \scriptsize \mid\;\cdot V \\[5pt] V\cdot \rho&=&m& \\[5pt] m&=&V\cdot \rho & \\[5pt] m&=&0,2848\,\text{m}^3\cdot 2,60\,\frac{\text{t}}{\text{m}^3}& \\[5pt] m&=&0,74048\,\text{t}\\[5pt] m&\approx&\underline{\underline{ 0,74\,\text{t}}} \end{array}$

Die Masse einer Stütze beträgt etwa $0,74\,\text{t}.$

Lösung 5

$\begin{array}[t]{rll} u&=&2e+2f+2g+2f+2e \\[5pt] u&=&\underline{\underline{ 4e+4f+2g}} \end{array}$

Wie viel Zentimeter Draht benötigt Ben mindestens?

Es gilt:

Länge von $e$ : $e=20\,\text{mm}$
Länge von $f$ : $f=2e=2\cdot 20\,\text{mm}=40\,\text{mm}$
Länge von $g$ : $g=3e=3\cdot 20\,\text{mm}=60\,\text{mm}$

Daraus folgt:

$\begin{array}[t]{rll} u&=&4e+4f+2g\\[5pt] u&=&4\cdot 20\,\text{mm}+4\cdot 40\,\text{mm}+2\cdot 60\,\text{mm}\\[5pt] u&=&360\,\text{mm}\\[5pt] u&=&\underline{\underline{ 36\,\text{cm}}} \end{array}$

Ben benötigt mindestens $36\,\text{cm}$ Draht.

Wie lang hat Carmen die Teilstrecken gewählt?

Formel zur Berechnung des Umfangs nach $e$ umformen:

$\begin{array}[t]{rll} u&=&4e+4f+2g\\[5pt] u&=&4e+4\cdot 2e+2\cdot 3e\\[5pt] u&=&18e &\quad \scriptsize \mid\;:18 \\[5pt] \dfrac{u}{18}&=&e \\[5pt] e&=&\dfrac{u}{18} \\[5pt] e&=&\dfrac{1,08\,\text{m}}{18} \\[5pt] e&=&0,06\,\text{m} \\[5pt] e&=&\underline{\underline{ 6\,\text{cm}}} \\[5pt] \end{array}$

Damit folgt für die anderen Teilstrecken:

$f=2e=2\cdot 6\,\text{cm}=\underline{\underline{ 12\,\text{cm}}}$
$g=3e=3\cdot 6\,\text{cm}=\underline{\underline{ 18\,\text{cm}}}$

Carmen hat für die Teilstrecken die folgenden Maße verwendet: $e=6\,\text{cm}, f=12\,\text{cm}$ und $g=18\,\text{cm}.$