Teil B – Pflichtaufgaben

Aufgabe 1

Auf dem Dach einer Oberschule wird mit einer Solaranlage elektrische Energie erzeugt.
Folgende Werte wurden in den einzelnen Zeiträumen für ein Jahr ermittelt.

Zeitraum	Energie in kWh
Frühlingsmonate
Sommermonate	$7\,716$
Herbstmonate	$4\,627$
Wintermonate
Gesamt	$22\,528$

Berechne, wie viel Prozent der gesamten Energie in den Sommermonaten erzeugt wurde.

In den Frühlingsmonaten wurden $35 \,\%$ der gesamten Energie erzeugt.

Berechne, wie viele Kilowattstunden Energie in diesen Monaten erzeugt wurden.
Stelle in einem Kreisdiagramm die Anteile der Energien der vier Zeiträume an der gesamten Energie dar.

Für Aufgabe 1 erreichbare BE: 6

Aufgabe 2

Gegeben sind zwei Funktionen $f$ und $g.$

$\begin{aligned} & y=f(x)=x^{-2} \quad(x \neq 0) \\ & y=g(x)=(x+1)^2-3\end{aligned}$

Übernimm die Wertetabelle für die Funktion $f$ und trage die fehlenden Werte ein.

$\color{#ffffff}{x}$	$\color{#ffffff}{y=f(x)}$
$-3$
$-2$
$-0,4$
$0,5$
$1$
$3$

Zeichne den Graphen der Funktion $f$ mit Hilfe der berechneten Wertepaare in ein rechtwinkliges Koordinatensystem.

Gib die Koordinaten des Scheitelpunktes der Funktion $g$ an.

Die Graphen der Funktionen $f$ und $g$ haben zwei Schnittpunkte $P$ und $Q.$
Der Schnittpunkt $P$ liegt im I. Quadranten.
Ermittle die Koordinaten des Schnittpunktes $P.$

Für Aufgabe 2 erreichbare BE: 6

Aufgabe 3

Löse die folgende Gleichung. Führe eine Probe durch.
$5+6(x-2)=35$

Gib die Lösungen der quadratischen Gleichung an.
$(x+3)(x-2)=0$

Ermittle einen Term zur Berechnung des Umfangs der abgebildeten achsensymmetrischen Figur und fasse diesen soweit wie möglich zusammen.

Abbildung (nicht maßstäblich)

Für Aufgabe 3 erreichbare BE: 6

Aufgabe 4

Ein Hochbeet in einer Gartenausstellung hat die Form eines Prismas mit dreieckiger Grundfläche.
Die Seiten der Grundfläche sind $7,50\,\text{m};$ $8,00 \,\text{m}$ und $9,50 \,\text{m}$ lang.
Der Rahmen des Hochbeetes ist $80 \,\text{cm}$ hoch.

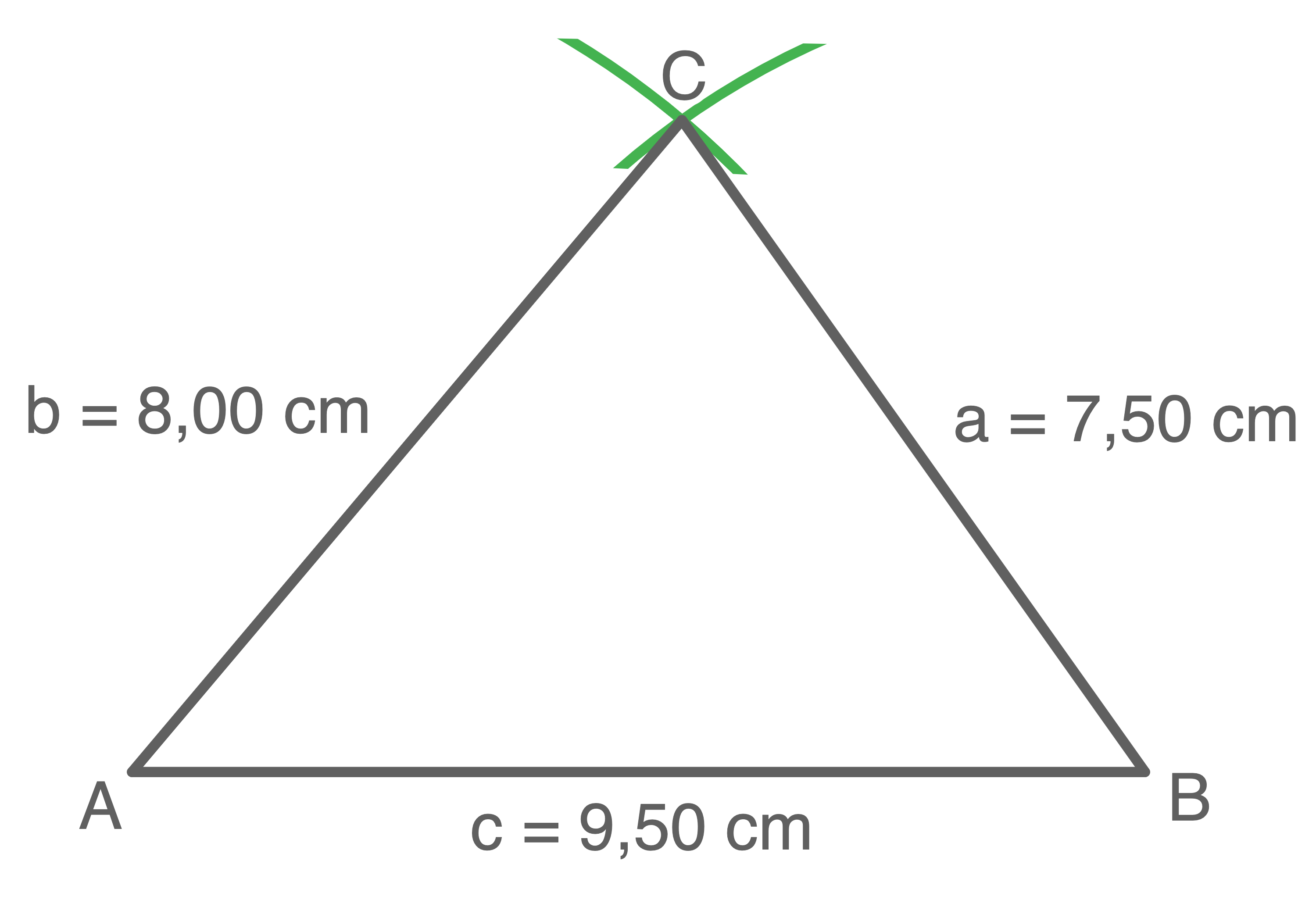
Konstruiere die Grundfläche des Hochbeetes in einem geeigneten Maßstab.

Berechne die Größe des größten Innenwinkels der Grundfläche des Hochbeetes.

Das Hochbeet ist schichtweise mit unterschiedlichen Naturmaterialien gefüllt.
Die oberste Schicht entspricht $\dfrac{2}{5}$ der Rahmenhöhe und besteht aus Erde.
Ermittle, mit wie viel Kubikmeter Erde das Hochbeet gefüllt ist.

Für Aufgabe 4 erreichbare BE: 6

Aufgabe 5

Beim Besuch eines Freizeitparkes erfassen die Jugendlichen einer 9. Klasse die Wartezeiten an der Achterbahn.
Diese Wartezeiten in Minuten stehen in der folgenden Urliste.

5	6
4	5
5	4
4	4
42	4
5	5
5	4
4	6
4	3
4	5

Übernimm die Häufigkeitstabelle und vervollständige diese.

Arithmetisches Mittel und Zentralwert sind statistische Kenngrößen und können zum Beschreiben der mittleren Wartezeit an der Achterbahn genutzt werden.

Berechne das arithmetische Mittel für diese Wartezeiten.
Gib den Zentralwert für diese Wartezeiten an.
Entscheide und begründe, welche der beiden statistischen Kenngrößen die mittlere Wartezeit an der Achterbahn besser beschreibt.

Für Aufgabe 5 erreichbare BE: 6

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

Lösungsweg über den Dreisatz

Dreisatz anzeigen

$7\,716\,\text{kWh} \mathrel{\widehat{=}} \underline{\underline{ 34,25 \,\%}}$

Lösungsweg über die Verhältnisgleichung

$\begin{array}[t]{rll} \dfrac{x}{7\,716\,\text{kWh}}&=&\dfrac{100\,\%}{22\,528\,\text{kWh}} \quad\quad\quad\quad \scriptsize \mid\;\cdot 7\,716\,\text{kWh} \\[5pt] x&=&\dfrac{100\,\%}{22\,528\,\text{kWh}}\cdot 7\,716\,\text{kWh} \\[5pt] x&\approx&\underline{\underline{ 34,25\,\%}} \end{array}$

Lösungsweg über die Prozentformel

$\begin{array}[t]{rll} p\,\%&=&\dfrac{W\cdot 100}{G}\,\% \\[5pt] p\,\%&=&\dfrac{7\,716\,\text{kWh}\cdot 100}{22\,528\,\text{kWh}}\,\% \\[5pt] p\,\%&\approx&\underline{\underline{ 34,25\,\% }} \end{array}$

Lösungsweg über den Dezimalbruch

$\dfrac{7\,716\,\text{kWh}}{22\,528\,\text{kWh}}\approx 0,3425=\underline{\underline{ 34,25\,\%}}$

In den Sommermonaten wurden etwa $34,25\,\%$ der gesamten Energie erzeugt.

Wie viele Kilowattstunden Energie wurden in den Frühlingsmonaten erzeugt?

Der Prozentwert zum Prozentsatz $35\,\%$ kann wieder über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.

Beispielhafter Lösungsweg über den Dezimalbruch

$22\,528\,\text{kWh}\cdot 0,35\approx\underline{\underline{ 7\,885\,\text{kWh}}}$

In den Frühlingsmonaten wurden etwa $7\,885\,\text{kWh}$ Energie erzeugt.

Kreisdiagramm erstellen

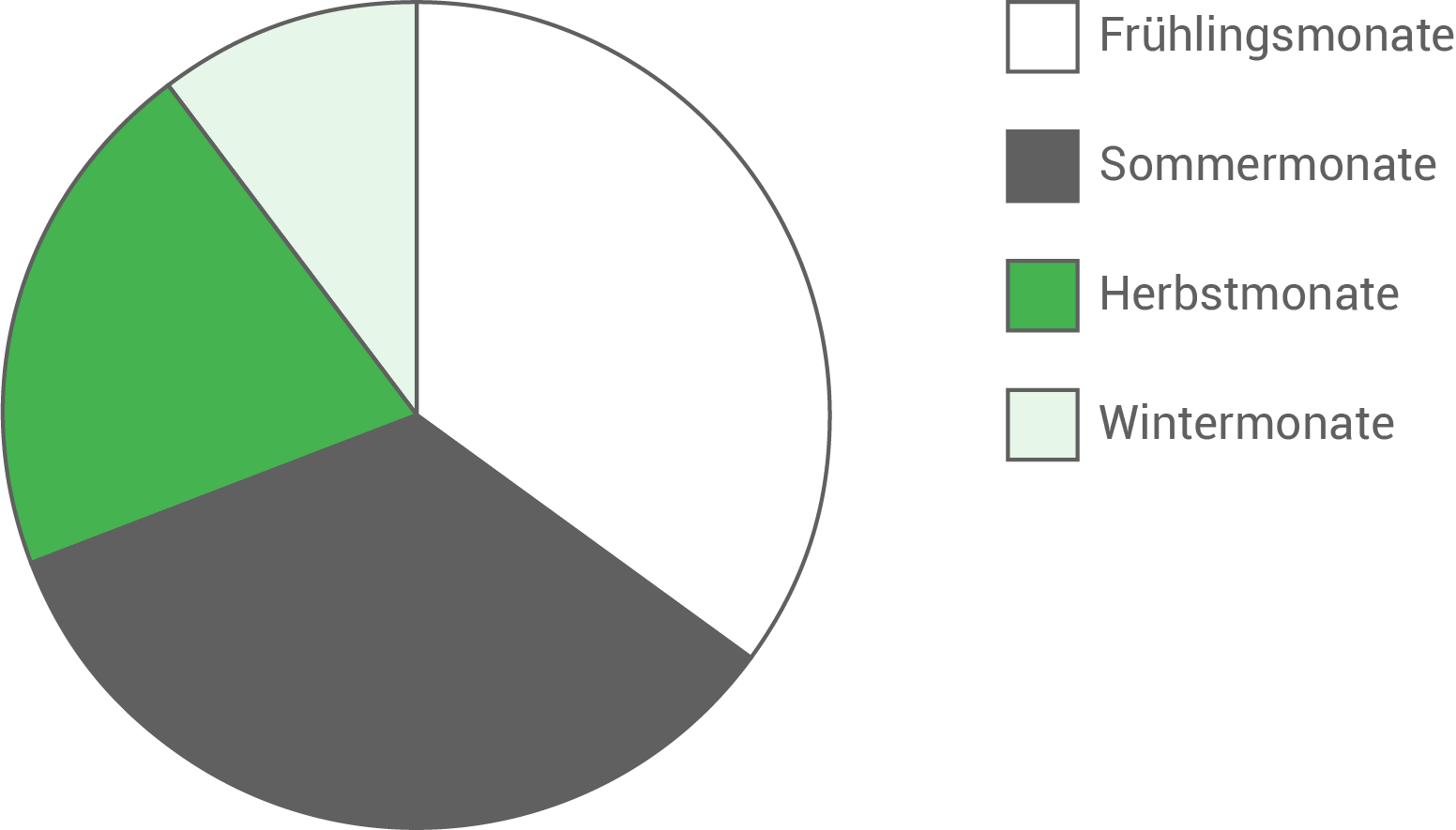
Zeitraum	Energie in kWh	Winkel für das Kreisdiagramm
Frühlingsmonate	$7\,885$	$\dfrac{7\,885}{22\,528}\cdot 360^{\circ}\approx126^{\circ}$
Sommermonate	$7\,716$	$\dfrac{7\,716}{22\,528}\cdot 360^{\circ}\approx123^{\circ}$
Herbstmonate	$4\,627$	$\dfrac{4\,627}{22\,528}\cdot 360^{\circ}\approx74^{\circ}$
Wintermonate		$360^{\circ}-126^{\circ}-123^{\circ}$ $-74^{\circ}=37^{\circ}$
Gesamt	$22\,528$	$360^\circ$

Mit diesen Angaben lässt sich das Kreisdiagramm zeichnen:

Lösung 2

Wertetabelle ergänzen

$f(-3)=(-3)^{-2}=\dfrac{1}{(-3)^2}=\dfrac{1}{9}\approx 0,11$
$f(-2)=(-2)^{-2}=\dfrac{1}{(-2)^2}=\dfrac{1}{4}= 0,25$
$f(-0,4)=(-0,4)^{-2}=\dfrac{1}{(-0,4)^2}=6,25$
$f(0,5)=0,5^{-2}=\dfrac{1}{0,5^2}=\dfrac{1}{0,25}=4$
$f(1)=1^{-2}=\dfrac{1}{1^2}=1$
$f(3)=3^{-2}=\dfrac{1}{3^2}=\dfrac{1}{9}\approx 0,11$

$\color{#ffffff}{x}$	$-3$	$-2$	$-0,4$	$0,5$	$1$	$3$
$\color{#ffffff}{y=f(x)}$	$0,11$	$0,25$	$6,25$	$4$	$1$	$0,11$

Graphen zeichnen

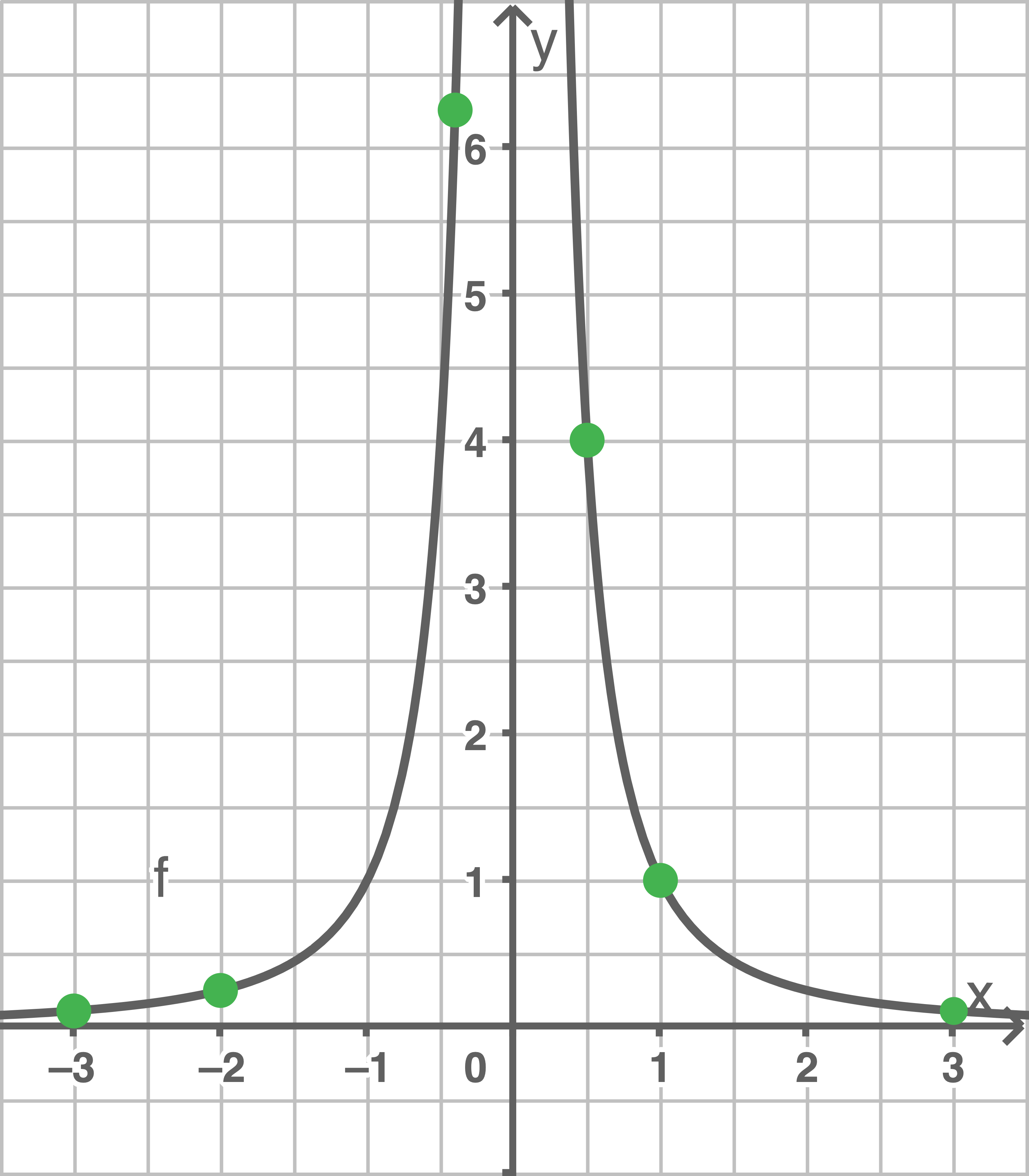
Funktionsgraph - Sachsen-Anhalt RSA 2023

Da die Funktion $g$ bereits in der Scheitelpunktform $y=(x+d)^2+e$ gegeben ist, kann der Scheitelpunkt $S(–d; e)$ abgelesen werden: $\underline{\underline{ S(-1\mid-3)}}$

Um die Koordinaten des Schnittpunktes $P$ zu ermitteln, wird der Graph der Funktin $g$ in das Koordinatensystem eingezeichnet und der Schnittpunkt im I. Quadranten abgelesen:

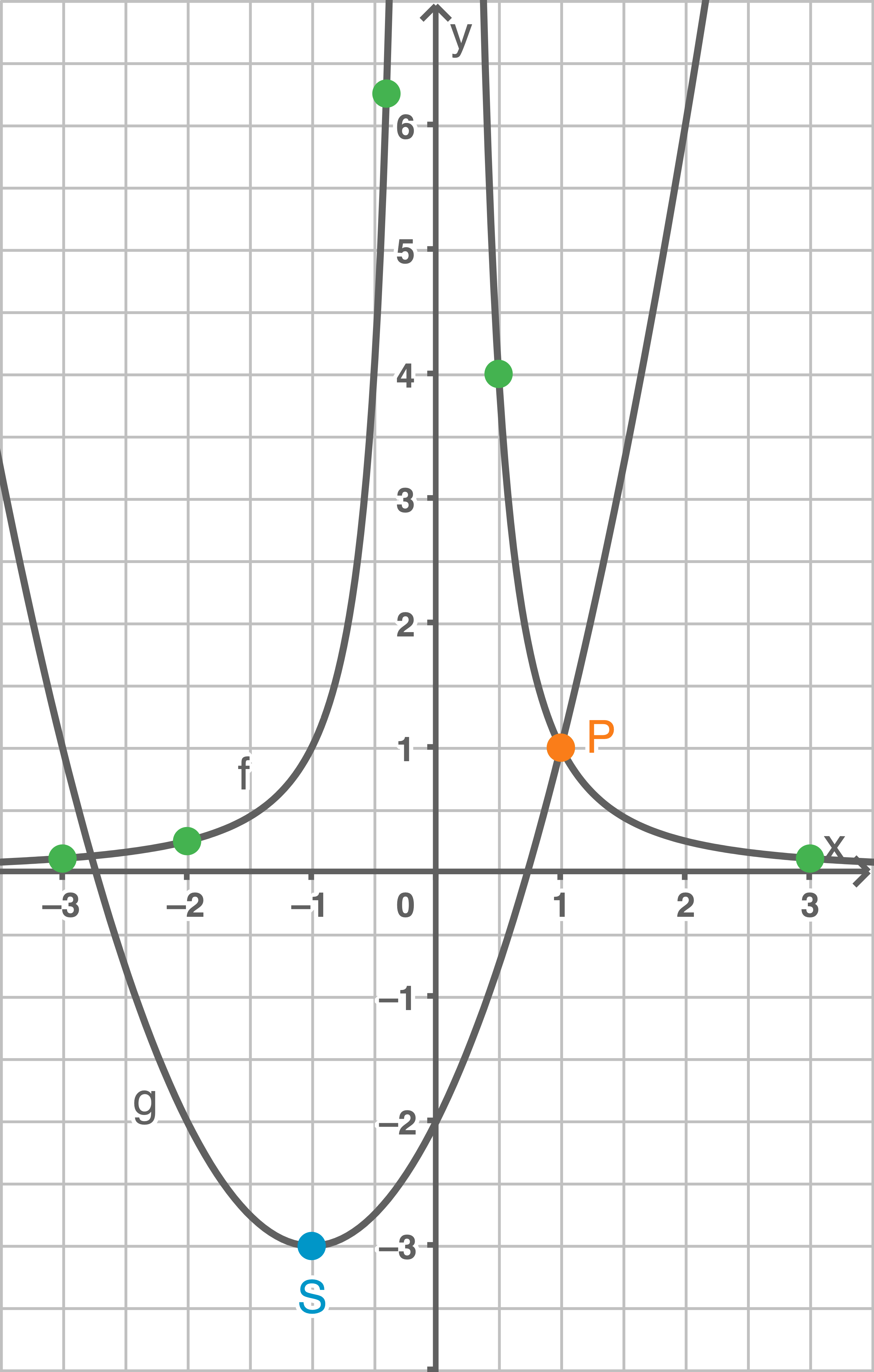Der Schnittpunkt im I. Quadranten lautet $\underline{\underline{ P(1;1)}}.$

Rechnerisch prüfen, ob sorgfältig gezeichnet wurde:

$\begin{array}[t]{rll} x^{-2}&=&(x+1)^2-3 \\[5pt] 1^{-2}&=&(1+1)^2-3 &\quad \scriptsize ? \\[5pt] 1&=&4-3 &\quad \scriptsize ? \\[5pt] 1&=&1 &\quad \scriptsize \text{wahr} \\[5pt] \end{array}$

Da die Probe eine wahre Aussage liefert, stimmt der Schnittpunkt $P(1;1).$

Lösung 3

Gleichung lösen

$\begin{array}[t]{rll} 5+6(x-2)&=& 35 \\[5pt] 5+6x-12&=& 35 \\[5pt] 6x-7&=& 35 &\quad \scriptsize \mid\;+7 \\[5pt] 6x&=& 42 &\quad \scriptsize \mid\;:6 \\[5pt] x&=& \underline{\underline{ 7}} \end{array}$

Probe durchführen

$\begin{array}[t]{rll} 5+6(x-2)&=& 35&\quad \scriptsize \\[5pt] 5+6(7-2)&=& 35&\quad \scriptsize ? \\[5pt] 5+6\cdot 5&=& 35&\quad \scriptsize ? \\[5pt] 35&=& 35&\quad \scriptsize \text{wahr} \\[5pt] \end{array}$

Eine Fallunterscheidung durchführen:

$(x+3)(x-2)=0$

1. Fall:

$\begin{array}[t]{rll} x+3&=&0 &\quad \scriptsize \mid\;-3 \\[5pt] x_1&=&\underline{\underline{ -3 }} \end{array}$

2. Fall:

$\begin{array}[t]{rll} x-2&=&0 &\quad \scriptsize \mid\;+2 \\[5pt] x_2&=&\underline{\underline{ 2 }} \end{array}$

Die quadratische Gleichung hat die Lösungen $x_1=-3$ und $x_2=2.$

$\begin{array}[t]{rll} u&=&2a+b+a+c+a+b+2a+b+c+b \\[5pt] u&=&\underline{\underline{ 6a+4b+2c }} \end{array}$

Lösung 4

Originallänge	Bildlänge im Maßstab 1:100
$7,50\,\text{m}$	$7,50\,\text{m}:100$ $=750\,\text{cm}:100=7,5\,\text{cm}$
$8,00\,\text{m}$	$8,00\,\text{m}:100$ $=800\,\text{cm}:100=8,0\,\text{cm}$
$9,50\,\text{m}$	$9,50\,\text{m}:100$ $=950\,\text{cm}:100=9,5\,\text{cm}$

Mit diesen Angaben kann das Dreieck konstruiert werden:

Der größte Innenwinkel liegt immer der längsten Seite gegenüber:

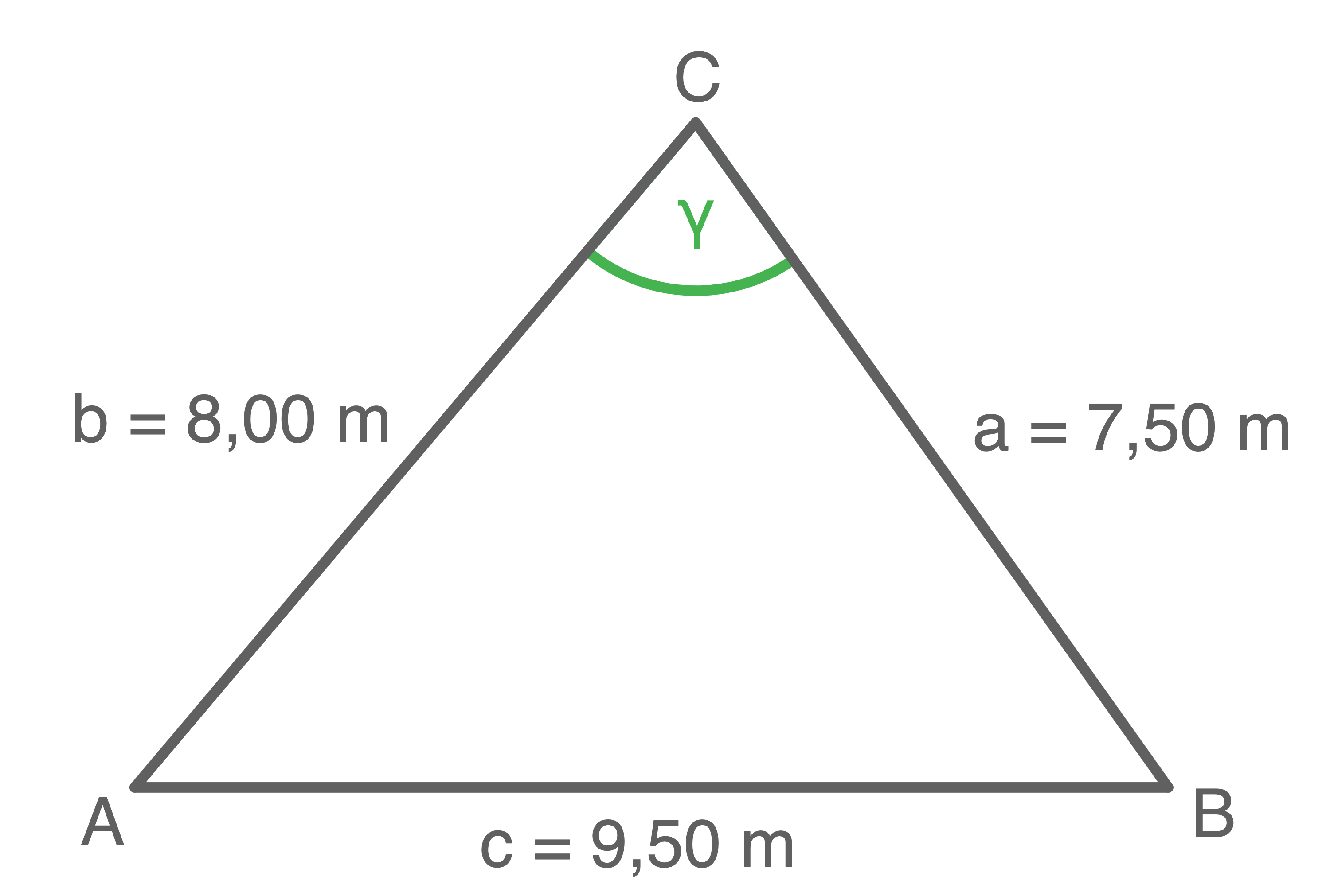Kosinussatz anwenden:

$c^2=a^2+b^2-2ab\cdot \cos\gamma \quad\quad\quad\quad\quad\quad \scriptsize \mid\;+2ab\cdot \cos\gamma$

$\begin{array}[t]{rll} c^2+2ab\cdot \cos\gamma&=&a^2+b^2&\quad \scriptsize \mid\;-c^2 \\[5pt] 2ab\cdot \cos\gamma&=&a^2+b^2-c^2&\quad \scriptsize \mid\;:2ab \\[5pt] \cos\gamma&=&\dfrac{a^2+b^2-c^2}{2ab} \\[5pt] \cos\gamma&=&\dfrac{7,5^2+8^2-9,5^2}{2\cdot 7,5\cdot 8} \\[5pt] \cos\gamma&=&0,25 &\quad \scriptsize \mid\;\cos^{-1} \\[5pt] \gamma&\approx&\underline{\underline{ 75,5^\circ}} \end{array}$

Höhe der obersten Schicht berechnen

$h=\dfrac{2}{5}\cdot 80\,\text{cm}=32\,\text{cm}=0,32\,\text{m}$

Grundflächeninhalt des Dreiecks berechnen

$\begin{array}[t]{rll} A_G&=&\dfrac{1}{2}\cdot ab\cdot \sin\gamma \\[5pt] A_G&=&\dfrac{1}{2}\cdot 7,50\,\text{m}\cdot 8,00\,\text{m}\cdot \sin 75,5^\circ \\[5pt] A_G&\approx &29,0\,\text{m}^2 \end{array}$

Volumen der obersten Schicht berechnen

$\begin{array}[t]{rll} V&=&A_G\cdot h \\[5pt] V&=&29,0\,\text{m}^2\cdot 0,32\,\text{m} \\[5pt] V&=&\underline{\underline{ 9,28\,\text{m}^3}} \end{array}$

Das Hochbeet ist mit etwa $9,28\,\text{m}^3$ Erde gefüllt.

Lösung 5

Wartezeit in min	Absolute Häufigkeit	Relative Häufigkeit
3	$1$	$\dfrac{1}{20}=0,05$
4	$9$	$\dfrac{9}{20}=0,45$
5	$7$	$\dfrac{7}{20}=0,35$
6	$2$	$\dfrac{2}{20}=0,10$
42	$1$	$\dfrac{1}{20}=0,05$
Summe	$20$	$1$

Arithmetisches Mittel berechnen

Um das arithmetische Mittel zu berechnen, wird die Summe aller Werte durch die Anzahl der Werte geteilt:

$\dfrac{1\cdot 3+9\cdot 4+7\cdot 5+2\cdot 6+1\cdot 42}{20}=\dfrac{128}{20}=\underline{\underline{ 6,4}}$

Das arithmetische Mittel der Wartezeiten beträgt $6,4\,\text{min}.$

Zentralwert angeben

Wartezeiten der Größe nach ordnen:

3
4
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
6
6
42

Da die Liste eine gerade Anzahl an Werten beinhaltet, werden die beiden Werte in der Mitte (grün markiert) addiert und das Ergebnis durch zwei geteilt:

$\dfrac{4+5}{2}\,\text{min}=\underline{\underline{ 4,5\,\text{min}}}$

Der Zentralwert der Wartezeiten beträgt $4,5\,\text{min}.$

Welche der beiden statistischen Kenngrößen beschreibt die mittlere Wartezeit an der Achterbahn besser?

Der Zentralwert beschreibt die mittlere Wartezeit besser, weil zehn Wartezeiten kleiner und zehn Wartezeiten größer als dieser Wert sind.
Das arithmetisches Mittel dagegen beschreibt die mittlere Wartezeit schlecht, weil 19 Wartezeiten kleiner und nur eine Wartezeit größer als dieser Wert sind.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?