Teil B – Pflichtaufgaben
Aufgabe 1
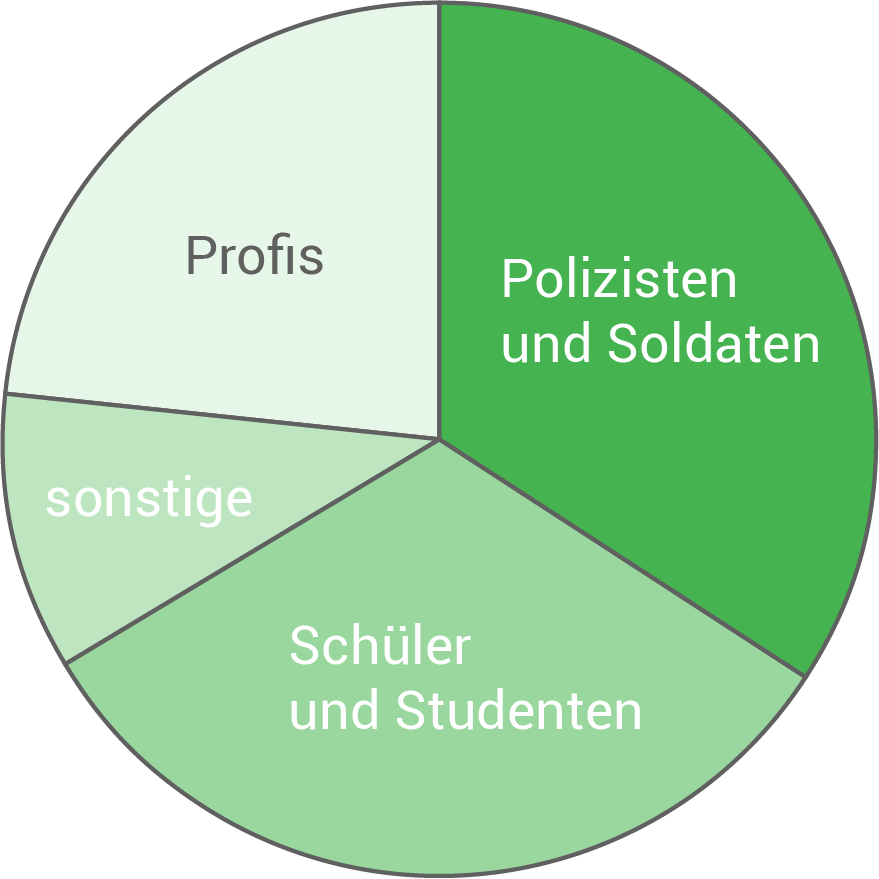
Insgesamt nahmen  Sportler für Deutschland an den Olympischen Spielen 2016 in Rio de Janeiro teil.
Sportler für Deutschland an den Olympischen Spielen 2016 in Rio de Janeiro teil.
In der Übersicht ist die Verteilung dieser Sportler auf ihre Berufsgruppen dargestellt. Sportler für Deutschland
In der Übersicht ist die Verteilung dieser Sportler auf ihre Berufsgruppen dargestellt. Sportler für Deutschland
| Berufsgruppe | Anzahl |
|---|---|
| Polizisten und Soldaten | |
| Schüler und Studenten | |
| sonstige Berufe | |
| Profis | ... |
a)
Gib an, wie viele Sportler aus jeder der vier Berufsgruppen teilnahmen.
b)
Berechne den prozentualen Anteil der Polizisten und Soldaten an der Gesamtzahl der Sportler für Deutschland.
c)
Stelle die Verteilung der Sportler auf die vier Berufsgruppen in einem Kreisdiagramm dar.
Für Aufgabe 1 erreichbare BE: 6
Aufgabe 2
a)
Zu der Funktion  mit der Gleichung
mit der Gleichung  gehört genau einer der Graphen
gehört genau einer der Graphen  bis
bis  (siehe Abbildung).
(siehe Abbildung).
Gib diesen Graphen an.
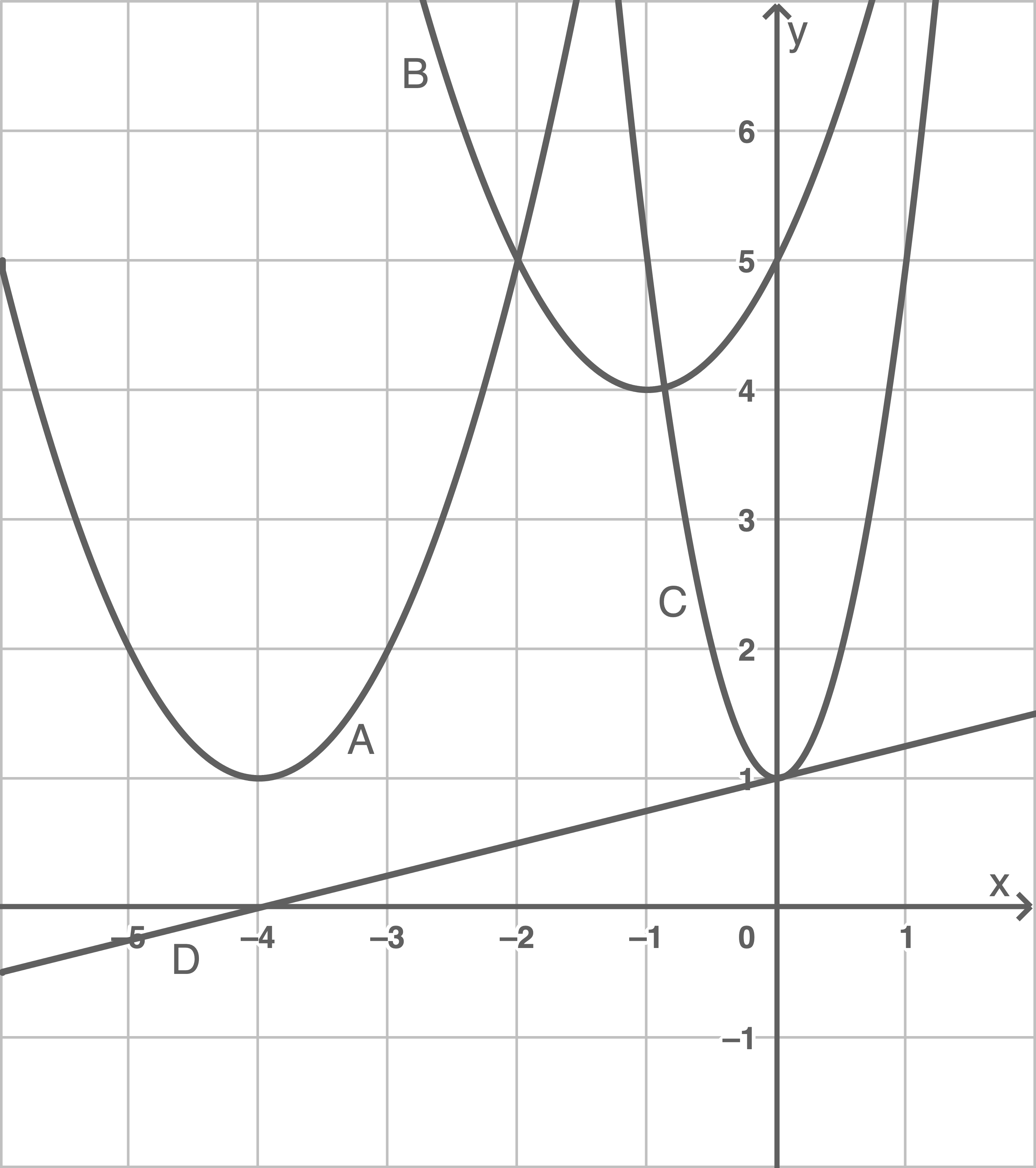
Gib diesen Graphen an.

b)
Gegeben ist die quadratische Funktion  mit der Gleichung
mit der Gleichung 
- Gib den Scheitelpunkt der Funktion
an.
- Zeichne den Graphen der Funktion
mindestens im Intervall
in ein rechtwinkliges Koordinatensystem.
- Der Graph der Funktion
wird im Koordinatensystem um
Einheiten nach rechts und um
Einheiten nach oben verschoben. Es entsteht der Graph der Funktion
Gib eine Funktionsgleichung der Funktionan.
c)
Von einer weiteren quadratischen Funktion  ist die Wertetabelle gegeben.
ist die Wertetabelle gegeben.
Der Graph der Funktion  hat die Form einer Normalparabel. Ermittle graphisch die Nullstellen der Funktion
hat die Form einer Normalparabel. Ermittle graphisch die Nullstellen der Funktion 
Für Aufgabe 2 erreichbare BE: 7
Aufgabe 3
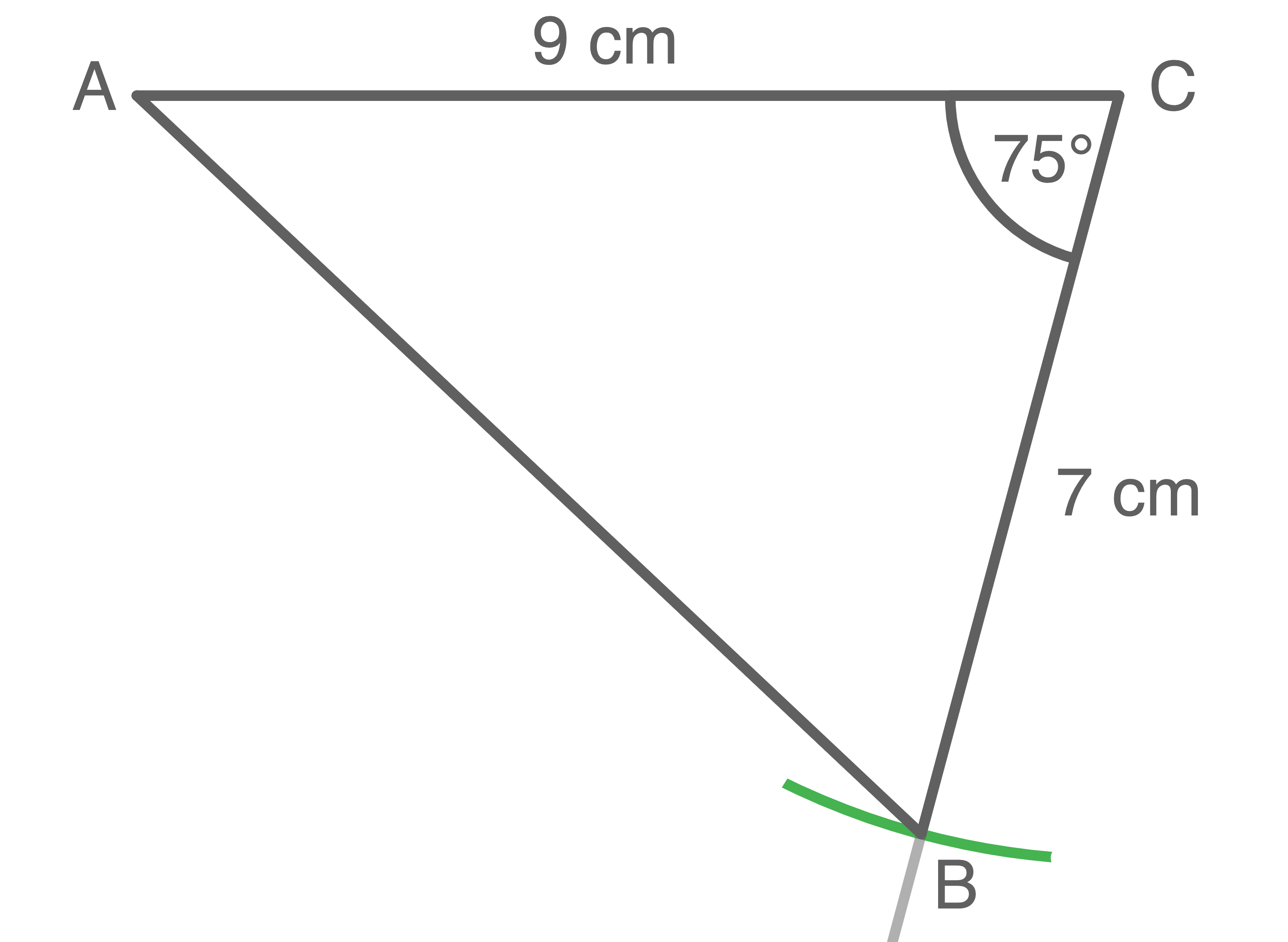
Herr Seifert pachtet für seine Ponys eine Weide. Diese hat die Form eines Dreiecks  mit den Seitenlängen
mit den Seitenlängen 
 und dem Winkel
und dem Winkel 
a)
Konstruiere das Dreieck  im Maßstab
im Maßstab 
b)
Herr Seifert möchte die Weide einzäunen.
Berechne die Länge des benötigten Zauns.
Berechne die Länge des benötigten Zauns.
c)
Die Pacht für die Weide beträgt 
Berechne, wie viel Pacht je Quadratmeter Herr Seifert bezahlt.
Berechne, wie viel Pacht je Quadratmeter Herr Seifert bezahlt.
Für Aufgabe 3 erreichbare BE: 7
Aufgabe 4
a)
Löse die Gleichung.

b)
Julius kann gedachte Zahlen erraten. Er stellt dazu seinen Freunden das folgende Zahlenrätsel.
„Denke dir eine natürliche Zahl.
Addiere zu deiner Zahl das -fache dieser Zahl.
-fache dieser Zahl.
Das Ergebnis teilst du durch
Nenne mir dein Endergebnis.“
Addiere zu deiner Zahl das
Das Ergebnis teilst du durch
Nenne mir dein Endergebnis.“
- Gib eine natürliche Zahl und das Endergebnis entsprechend des Zahlenrätsels an.
- Begründe, dass die gedachte Zahl immer die Hälfte des Endergebnisses ist.
Für Aufgabe 4 erreichbare BE: 4
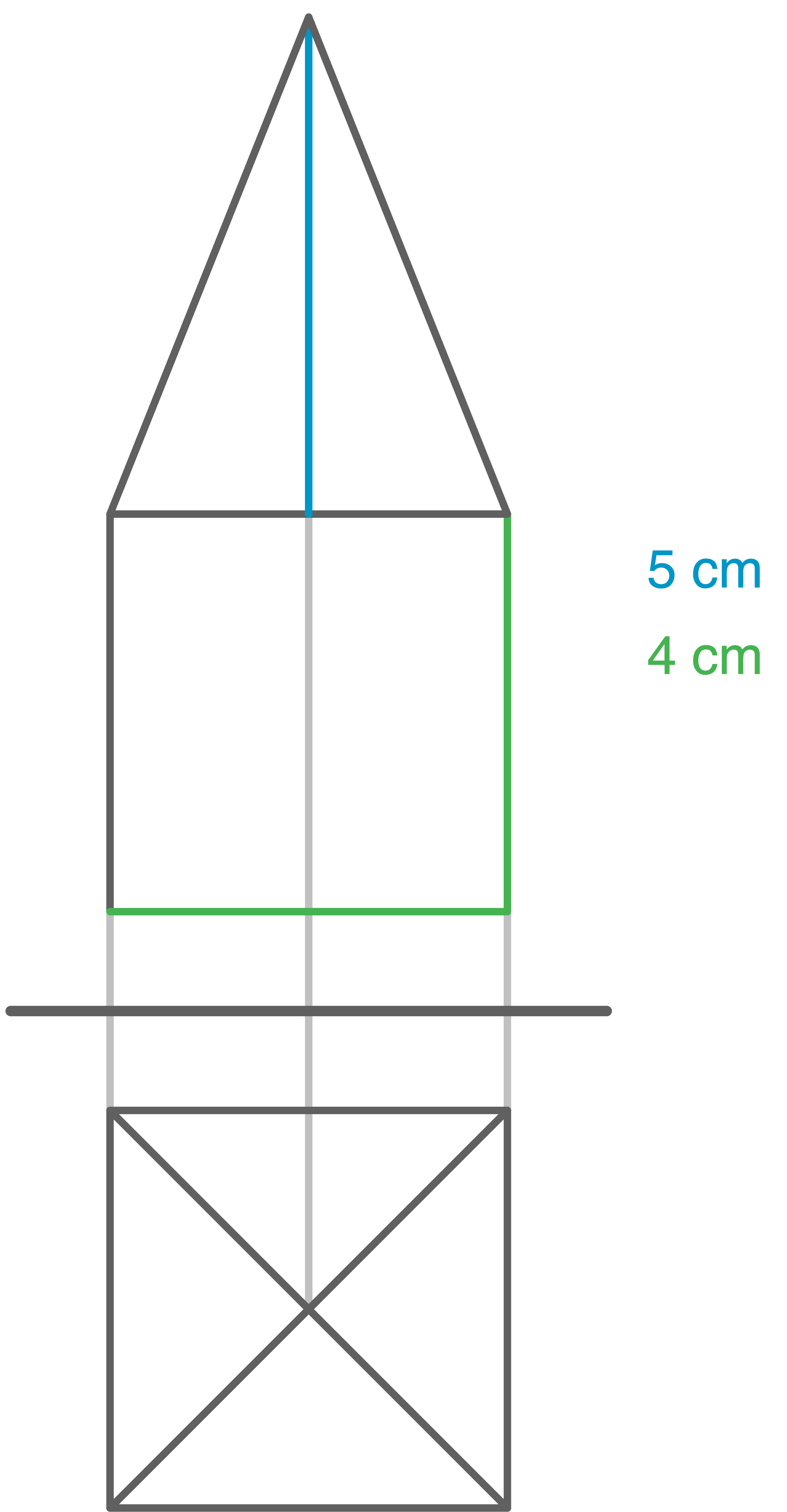
Aufgabe 5
Ein Körper wurde aus zwei Teilkörpern zusammengesetzt. Die Abbildung zeigt das Netz dieses Körpers.
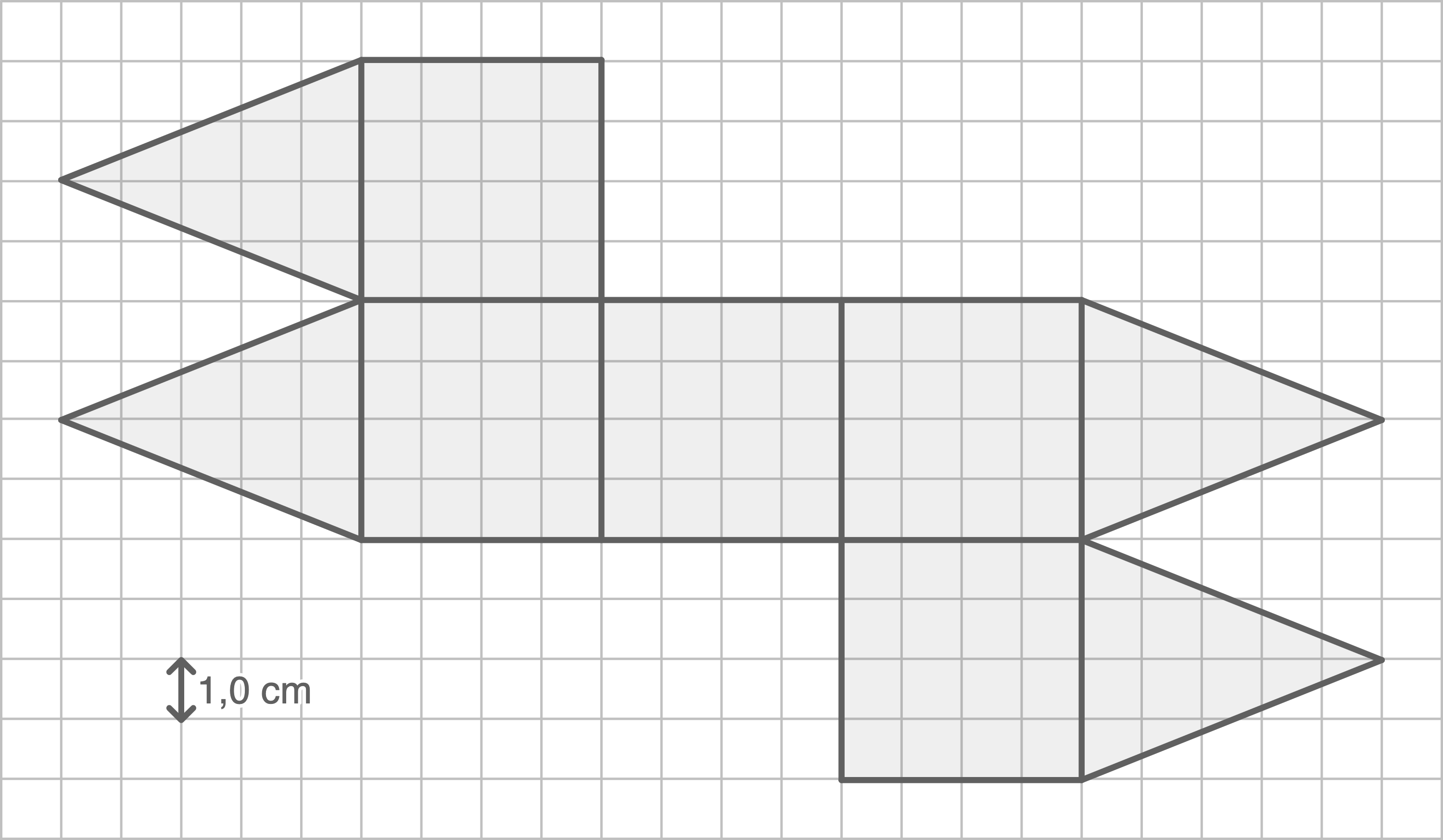

Abbildung im Quadratraster
a)
Benenne die beiden Teilkörper.
b)
Berechne das Volumen des Körpers.
c)
Zeichne ein Zweitafelbild des Körpers.
Für Aufgabe 5 erreichbare BE: 6
Lösung 1
a)
| Berufsgruppe | Anzahl |
|---|---|
| Polizisten und Soldaten | |
| Schüler und Studenten | |
| sonstige Berufe | |
| Profis | ...
|
b)
Lösungsweg über den Dreisatz




![\(\begin{array}{rcl}
450 & \mathrel{\widehat{=}}& 100\,\%\\[5pt]
1 & \mathrel{\widehat{=}}& \dfrac{100}{450}\,\%\\[5pt]
154 & \mathrel{\widehat{=}}& \dfrac{100}{450}\cdot 154\,\%\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/fc443fbaf0c14f0d8edb03588d3154218a67b876c3da40f12aa8027077103576_light.svg)





Lösungsweg über die Verhältnisgleichung
![\(\begin{array}[t]{rll}
\dfrac{x}{154}&=&\dfrac{100\,\%}{450} &\quad \scriptsize \mid\;\cdot 154 \\[5pt]
x&=&\dfrac{100\,\%}{450}\cdot 154 &\\[5pt]
x&\approx&\underline{\underline{ 34,2\,\%}}
\end{array}\)](https://www.schullv.de/resources/formulas/a48c19ecc7e3585c8b3b2585d48dd0ac8ac80ae05b63213bbe36d7a1ad4de4fb_light.svg)
Lösungsweg über die Prozentformel
![\(\begin{array}[t]{rll}
p\,\%&=&\dfrac{W\cdot 100}{G}\,\% \\[5pt]
p\,\%&=&\dfrac{154\cdot 100}{450}\,\% \\[5pt]
p\,\%&\approx&\underline{\underline{ 34,2\,\%}}
\end{array}\)](https://www.schullv.de/resources/formulas/be58032219957dc5000c8bf64a6f8a429b0c3b50e9a7845e6db72157edc4f786_light.svg)
Lösungsweg über den Dezimalbruch

Der prozentuale Anteil der Polizisten und Soldaten an der Gesamtzahl der Sportler beträgt
c)
| Berufsgruppe | Anzahl | Winkelgröße |
|---|---|---|
| Polizisten und Soldaten | ||
| Schüler und Studenten | ||
| sonstige Berufe | ||
| Profis |
Lösung 2
a)
b)
Scheitelpunkt der Funktion  angeben
Die allgemeine Funktionsgleichung einer quadratische Funktion ist
angeben
Die allgemeine Funktionsgleichung einer quadratische Funktion ist  Der Scheitelpunkt
Der Scheitelpunkt  hat die Koordinaten
hat die Koordinaten  und
und  Daraus folgt:
Daraus folgt:
 ist
ist  Graphen der Funktion zeichnen
Da in der Gleichung der Funktion
Graphen der Funktion zeichnen
Da in der Gleichung der Funktion  kein Faktor vor dem
kein Faktor vor dem  steht, handelt es sich um eine verschobene Normalparabel. Mit dem Scheitelpunkt
steht, handelt es sich um eine verschobene Normalparabel. Mit dem Scheitelpunkt  und der Schablone lässt sich der Graph von
und der Schablone lässt sich der Graph von  zeichnen:
zeichnen:
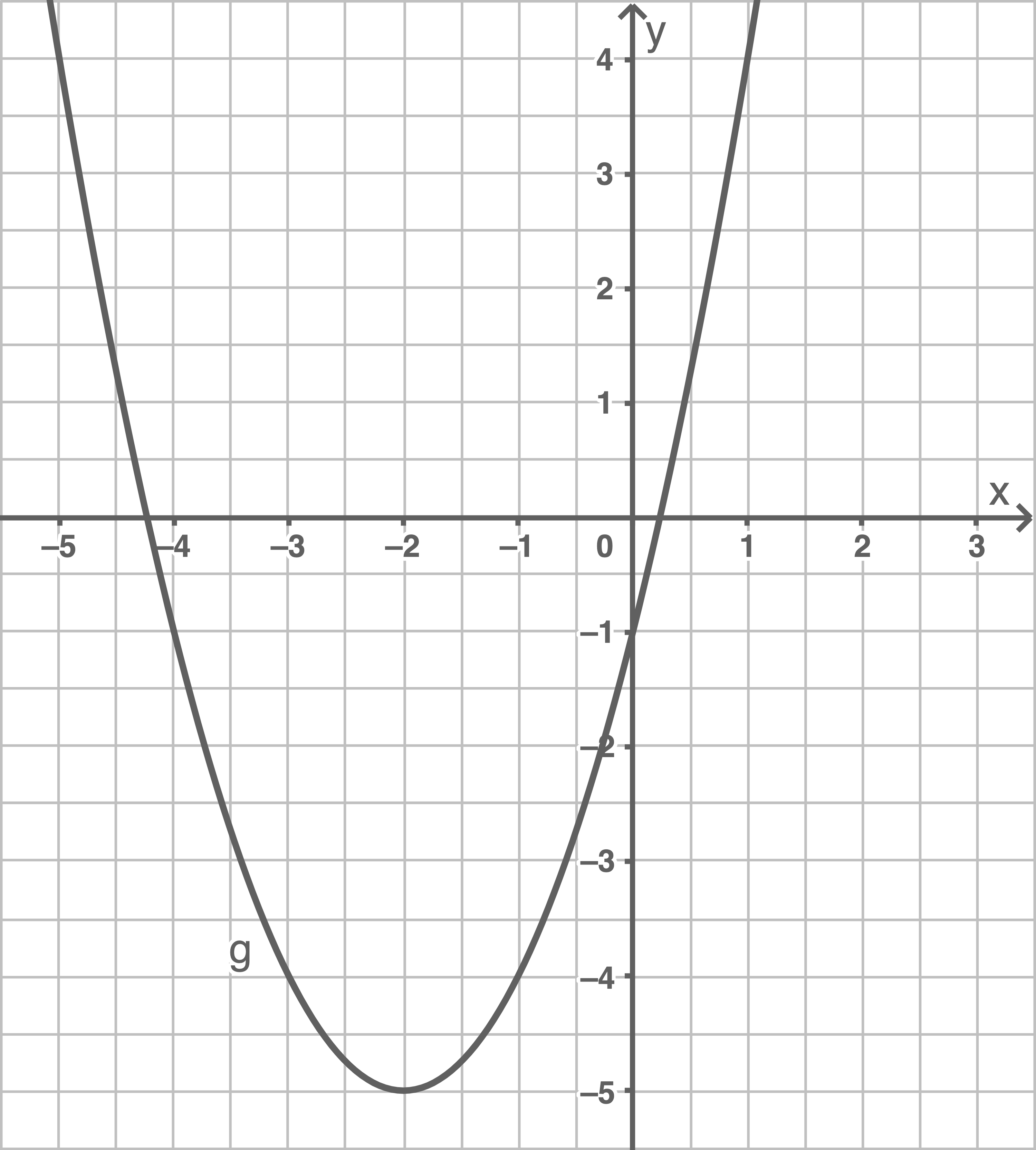 Eine Funktionsgleichung der Funktion
Eine Funktionsgleichung der Funktion  angeben
angeben


c)
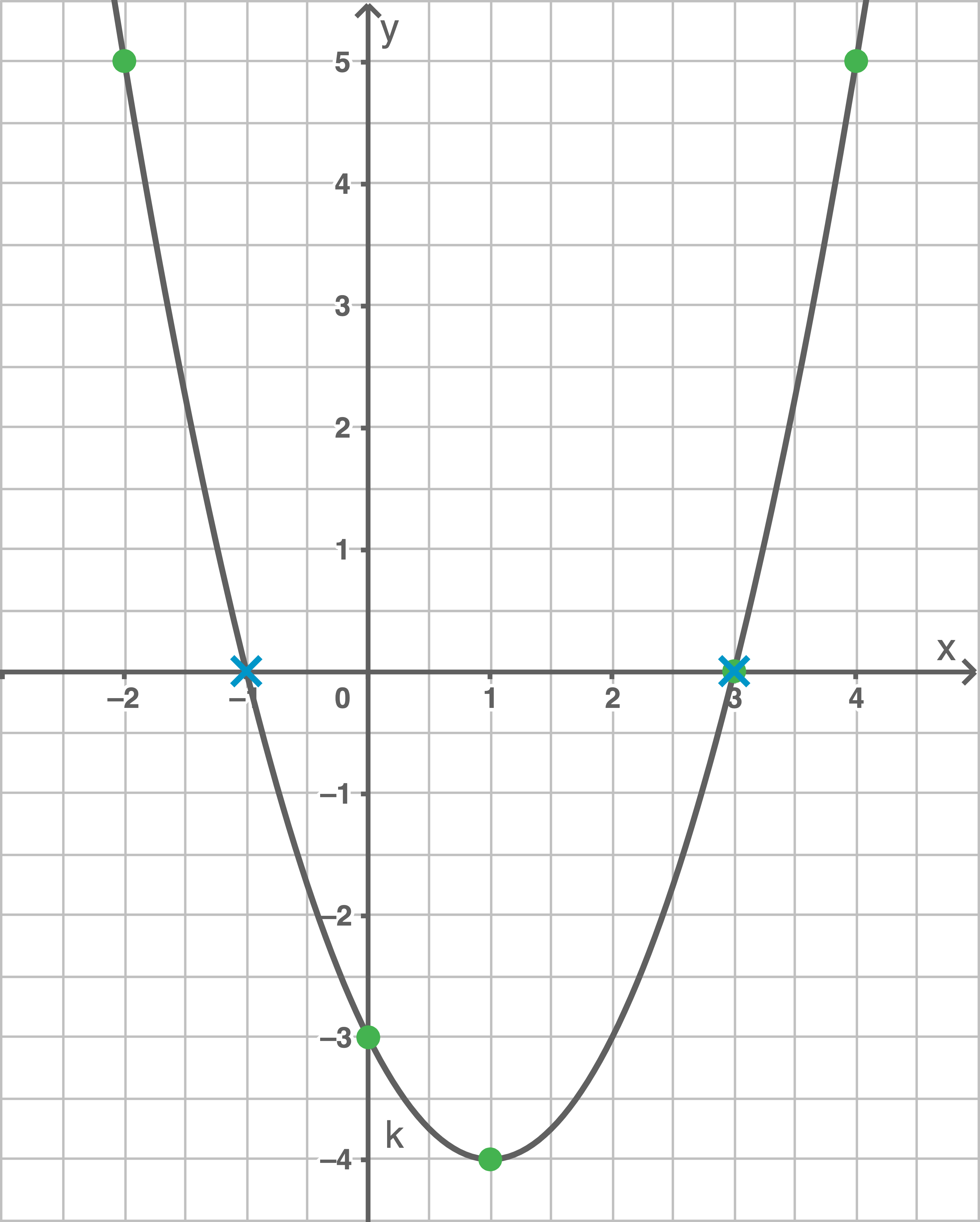
Lösung 3
a)
| Originallänge | Bildlänge im Maßstab 1:3000 |
|---|---|
b)
Länge der Strecke  berechnen
Kosinussatz anwenden:
berechnen
Kosinussatz anwenden:
![\(\begin{array}[t]{rll}
c^2&=&a^2+b^2-2\cdot a\cdot b\cdot \cos\gamma \quad\quad\quad\quad\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
c&=&\sqrt{a^2+b^2-2\cdot a\cdot b\cdot \cos\gamma} \\[5pt]
c&=&\sqrt{210^2+270^2-2\cdot 210\cdot 270\cdot \cos 75^\circ}\\[5pt]
c&\approx&296
\end{array}\)](https://www.schullv.de/resources/formulas/a3e7260e5cebdfc61007e832ff52c11f60239f7409fbc8661e6862d9b3359a77_light.svg) Länge des Zauns berechnen
Länge des Zauns berechnen
![\(\begin{array}[t]{rll}
u&=&a+b+c \\[5pt]
u&=&210\,\text{m}+270\,\text{m}+296\,\text{m} \\[5pt]
u&=&\underline{\underline{ 776\,\text{m}}}
\end{array}\)](https://www.schullv.de/resources/formulas/0b7c7e3929935b537ac21c5e7659a84df11a353cfc65d2bf56e1a7ad740811b0_light.svg) Die Länge des Zauns beträgt
Die Länge des Zauns beträgt 
c)
Flächeninhalt der Weide berechnen
![\(\begin{array}[t]{rll}
A&=&\dfrac{1}{2}\cdot a\cdot b\cdot \sin\gamma\\[5pt]
A&=&\dfrac{1}{2}\cdot 210\,\text{m}\cdot 270\,\text{m}\cdot \sin 75^\circ\\[5pt]
A&\approx&27\,384\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/0078edbd3ec6d6c66ec76cc8d9e515eb9ae334fd5932b861e90ef1351d35a4e3_light.svg) Pacht pro Quadratmeter berechnen
Pacht pro Quadratmeter berechnen
 Herr Seifert bezahlt
Herr Seifert bezahlt  Pacht pro Quadratmeter.
Pacht pro Quadratmeter.
Lösung 4
a)
b)
Eine natürliche Zahl und das Endergebnis angeben
Eine mögliche Zahl:  Für
Für  ergibt sich folgendes Endergebnis des Zahlenrätsels:
ergibt sich folgendes Endergebnis des Zahlenrätsels:
 eingesetzt:
eingesetzt:
- „Addiere zu deiner Zahl das
-fache dieser Zahl“:
- „Das Ergebnis teilst du durch
“:
- „Addiere zu deiner Zahl das
-fache dieser Zahl“:
- „Das Ergebnis teilst du durch
“:
Lösung 5
a)
Skizze des zusammengesetzten Körpers:
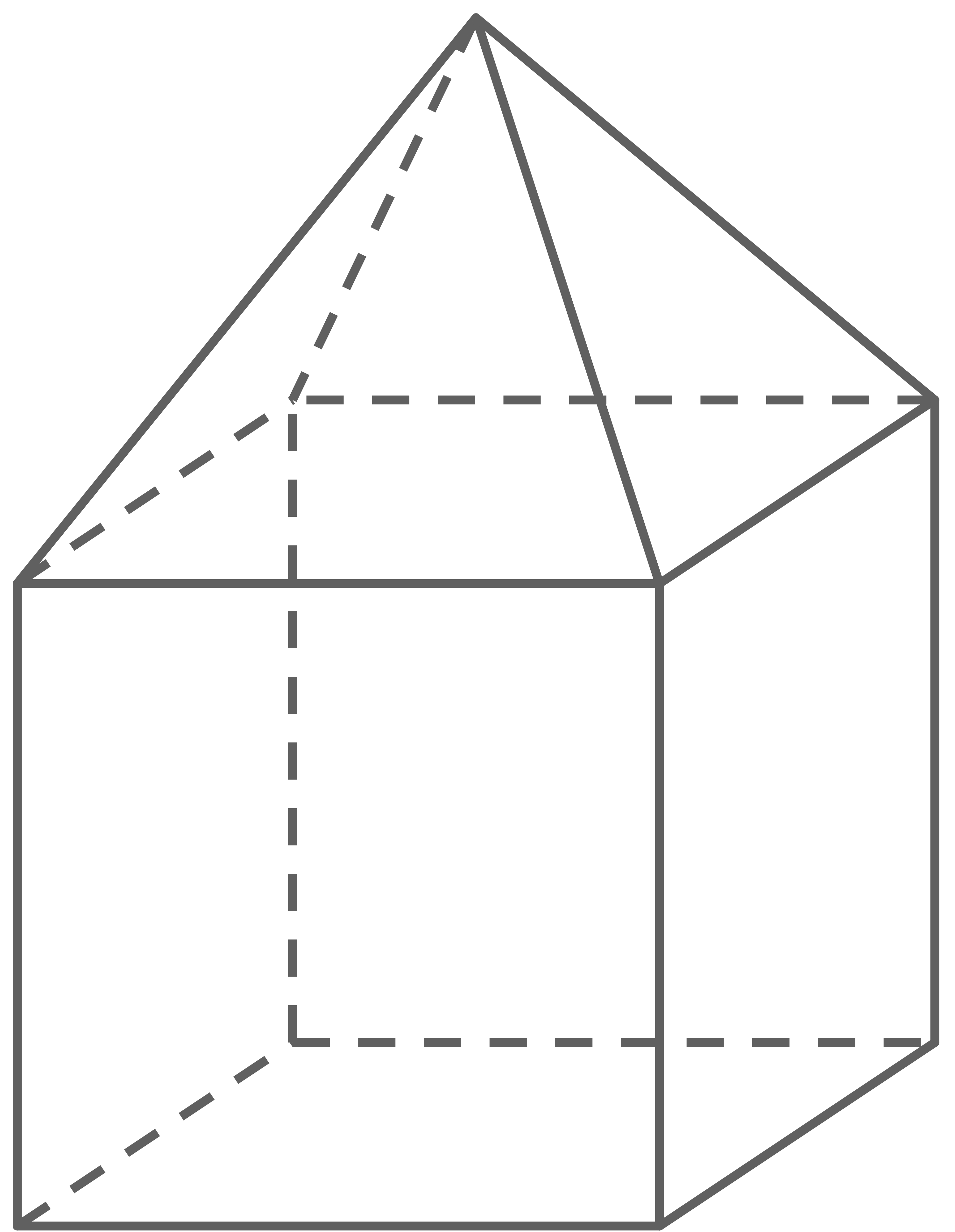 Daraus folgt:
Daraus folgt:

- Unterer Teilkörper: Würfel
- Oberer Teilkörper: Gerade quadratische Pyramide
b)
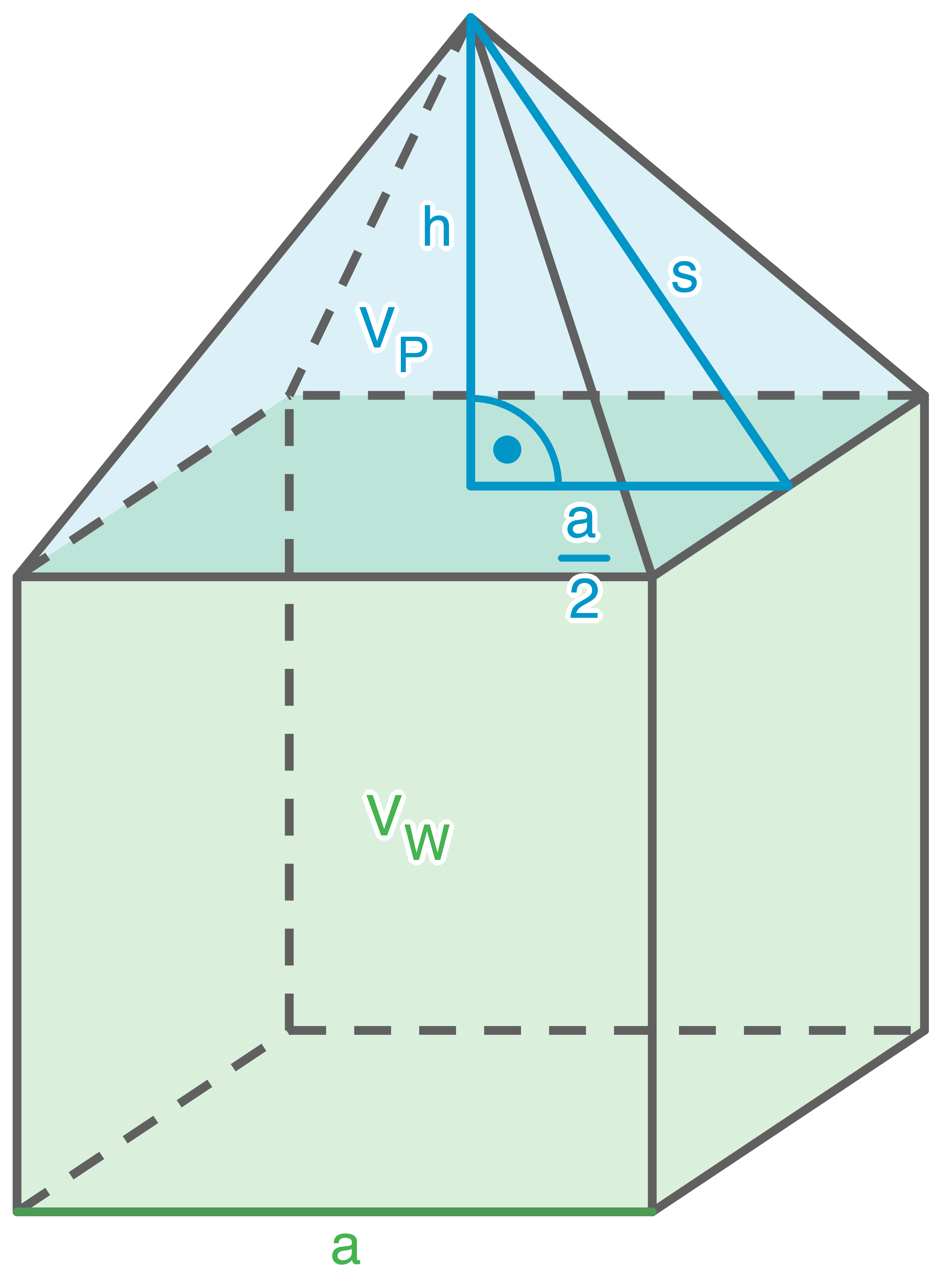
c)