Teil B – Pflichtaufgaben
Aufgabe 1
Für ihre Ausbildung benötigt Franka ein Notebook, einen Rucksack und einen Eingabestift.


a)
Berechne den prozentualen Anteil des Preises für das Notebook am Gesamtpreis der benötigten Waren.
b)
Ein Händler bietet in der Werbeaktion am Tag seines 11-jährigen Geschäftsjubiläums alle Waren  günstiger an.
günstiger an.
Berechne den Gesamtpreis, den Franka an diesem Tag bezahlen muss.
Berechne den Gesamtpreis, den Franka an diesem Tag bezahlen muss.
c)
Für einen Betrag von  muss Franka ihren Überziehungskredit
muss Franka ihren Überziehungskredit  Tage in Anspruch nehmen. Der Zinssatz beträgt
Tage in Anspruch nehmen. Der Zinssatz beträgt  pro Jahr.
pro Jahr.
Berechne die Zinsen, die Franka dafür bezahlen muss.
Berechne die Zinsen, die Franka dafür bezahlen muss.
Für Aufgabe 1 erreichbare BE: 6
Aufgabe 2
Gegeben sind zwei quadratische Funktionen  und
und  .
.
Die Gleichung der Funktion lautet
lautet 
Der Graph der Funktion ist eine nach oben geöffnete Normalparabel mit dem Scheitelpunkt
ist eine nach oben geöffnete Normalparabel mit dem Scheitelpunkt 
Die Gleichung der Funktion
Der Graph der Funktion
a)
Berechne die Nullstellen der Funktion  .
.
b)
Gib die Gleichung der Funktion  in der Scheitelpunktsform
in der Scheitelpunktsform  an.
an.
c)
Zeichne die Graphen der Funktionen  und
und  in ein rechtwinkliges Koordinatensystem mindestens im Intervall
in ein rechtwinkliges Koordinatensystem mindestens im Intervall 
Für Aufgabe 2 erreichbare BE: 6
Aufgabe 3
Forstwirtin Maier pflanzt Bäume auf einem dreieckigen Waldstück, das durch drei unterschiedlich lange Wege begrenzt wird.
Die Wege werden vereinfacht als Seiten eines Dreiecks betrachtet.
Die längste Seite ist lang und die kürzeste Seite
lang und die kürzeste Seite 
Der Winkel, der der längsten Seite gegenüberliegt, hat eine Größe von
Die Wege werden vereinfacht als Seiten eines Dreiecks betrachtet.
Die längste Seite ist
Der Winkel, der der längsten Seite gegenüberliegt, hat eine Größe von
a)
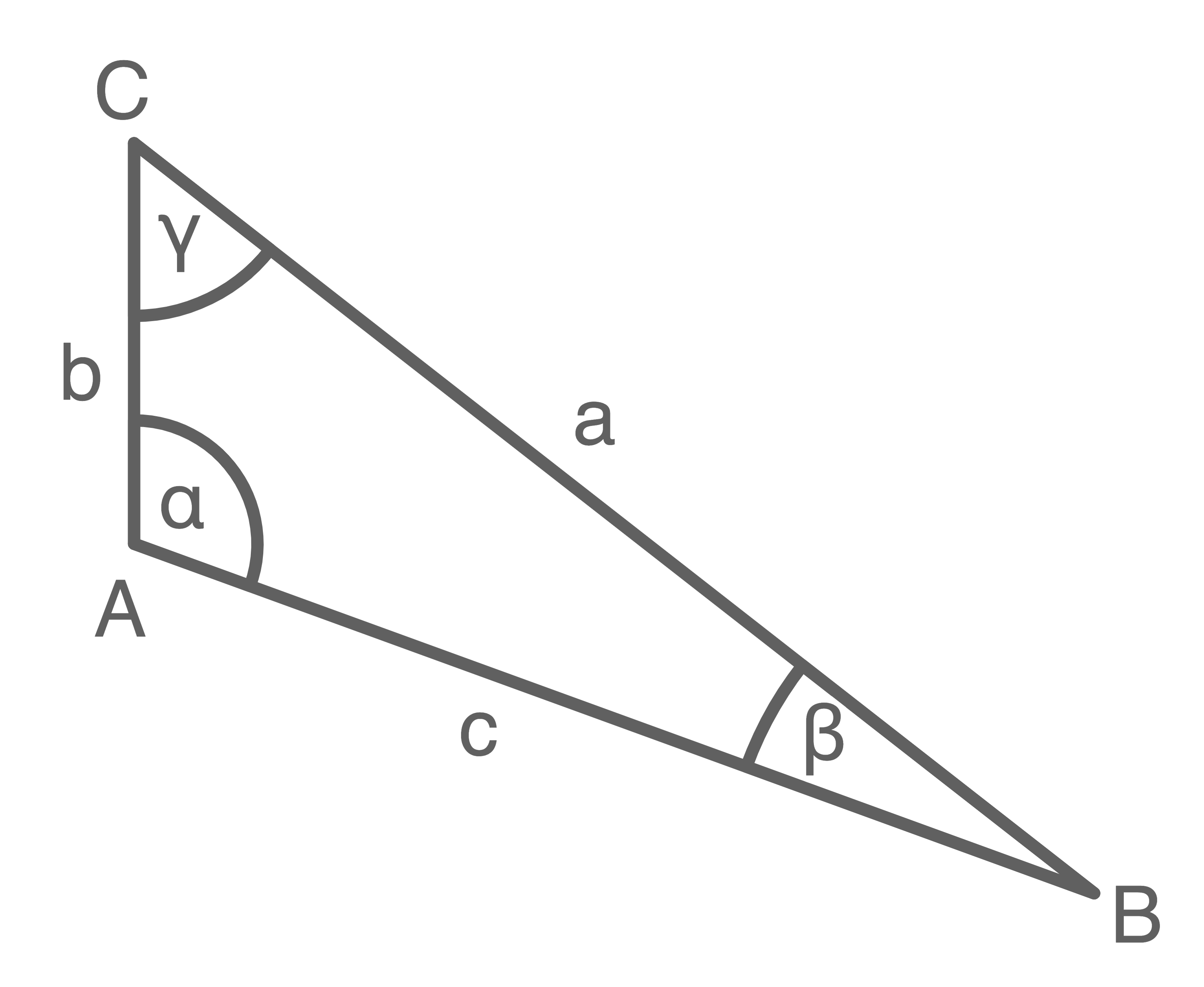
Skizziere ein entsprechendes Dreieck und trage die gegebenen Werte ein.
b)
Zeichne ein solches Dreieck im Maßstab 
c)
Um das gesamte Waldstück soll ein Zaun zum Schutz der Bäume vor Fraß durch Wildtiere gebaut werden.
Berechne die Länge des Zauns.
Berechne die Länge des Zauns.
Für Aufgabe 3 erreichbare BE: 6
Aufgabe 4
In einem Gefäß befinden sich drei gelbe Kugeln, zwei schwarze und eine rote Kugel. Lena zieht nacheinander zwei Kugeln. Die zuerst gezogene Kugel legt sie vor dem Ziehen der zweiten Kugel wieder zurück.
Das Ziehen der Kugeln ist ein zweistufiges Zufallsexperiment.
Das Ziehen der Kugeln ist ein zweistufiges Zufallsexperiment.
a)
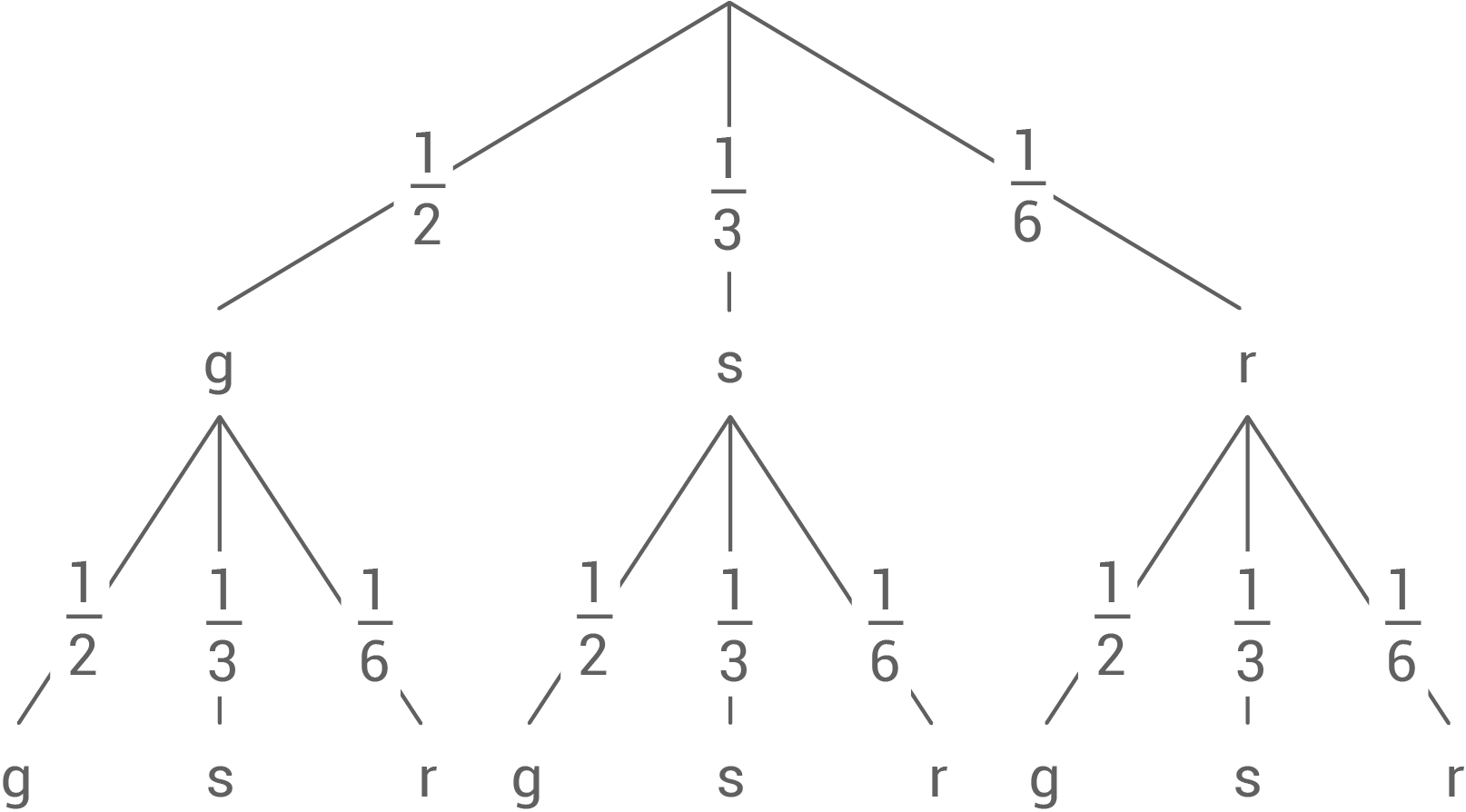
Zeichne für dieses Zufallsexperiment ein Baumdiagramm und trage alle Wahrscheinlichkeiten ein.
b)
Berechne die Wahrscheinlichkeit für das folgende Ergebnis:
Lena zieht zweimal die rote Kugel.
Lena zieht zweimal die rote Kugel.
c)
Berechne die Wahrscheinlichkeit für das folgende Ergebnis:
Lena zieht zwei Kugeln mit unterschiedlichen Farben.
Lena zieht zwei Kugeln mit unterschiedlichen Farben.
Für Aufgabe 4 erreichbare BE: 6
Aufgabe 5
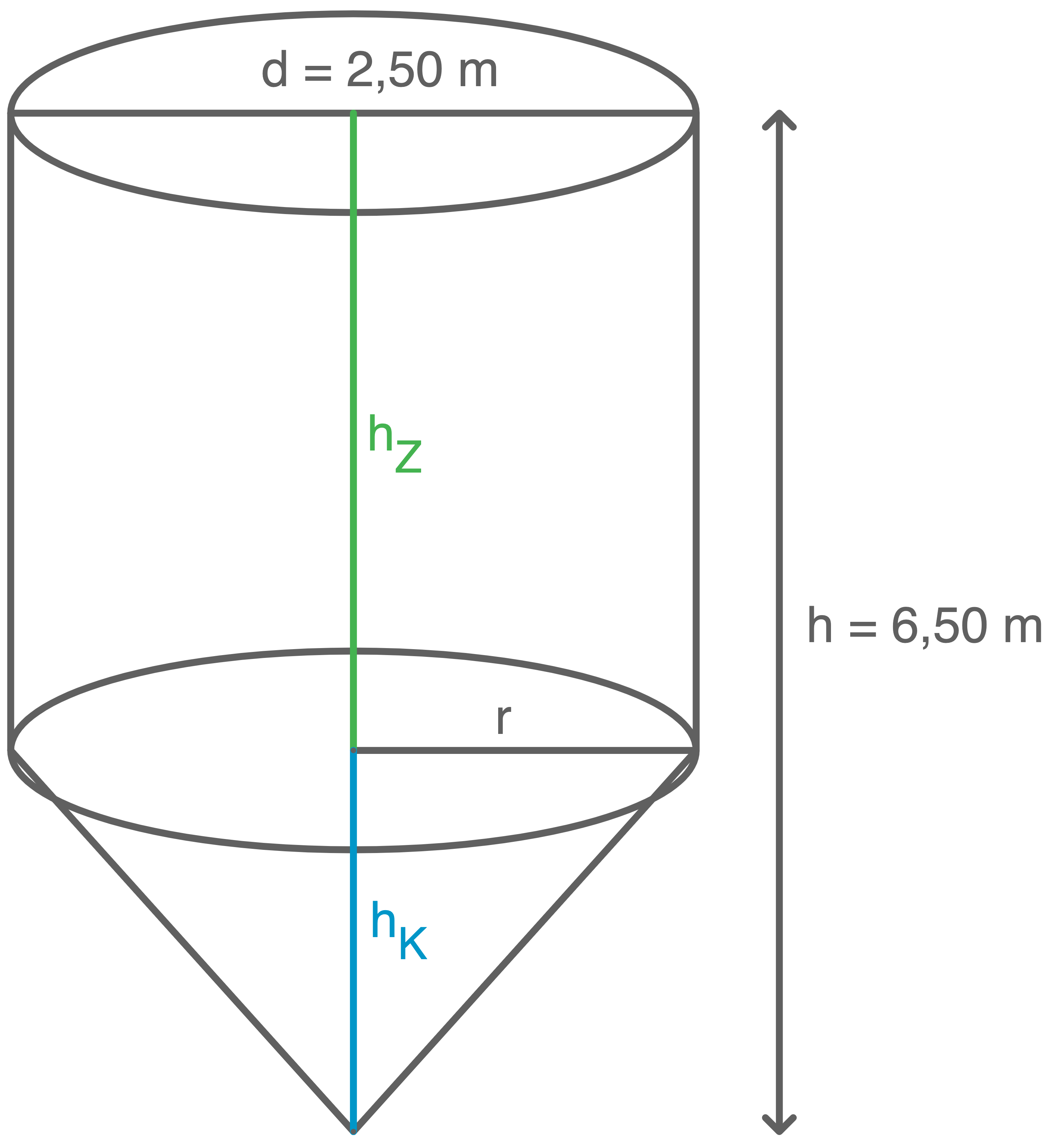
Bei der Sanierung einer Schule werden zur besseren Isolierung neue Dämmplatten angebracht. Diese werden mit Baukleber befestigt, welcher in einem Silo angeliefert wird (siehe Abbildung).
Dieses Silo wird vereinfacht als ein zusammengesetzter Körper aus einem Kreiskegel und einem Kreiszylinder betrachtet.
Die Gundflächen der beiden Teilkörper sind zueinander kongruent.
Die Gundflächen der beiden Teilkörper sind zueinander kongruent.
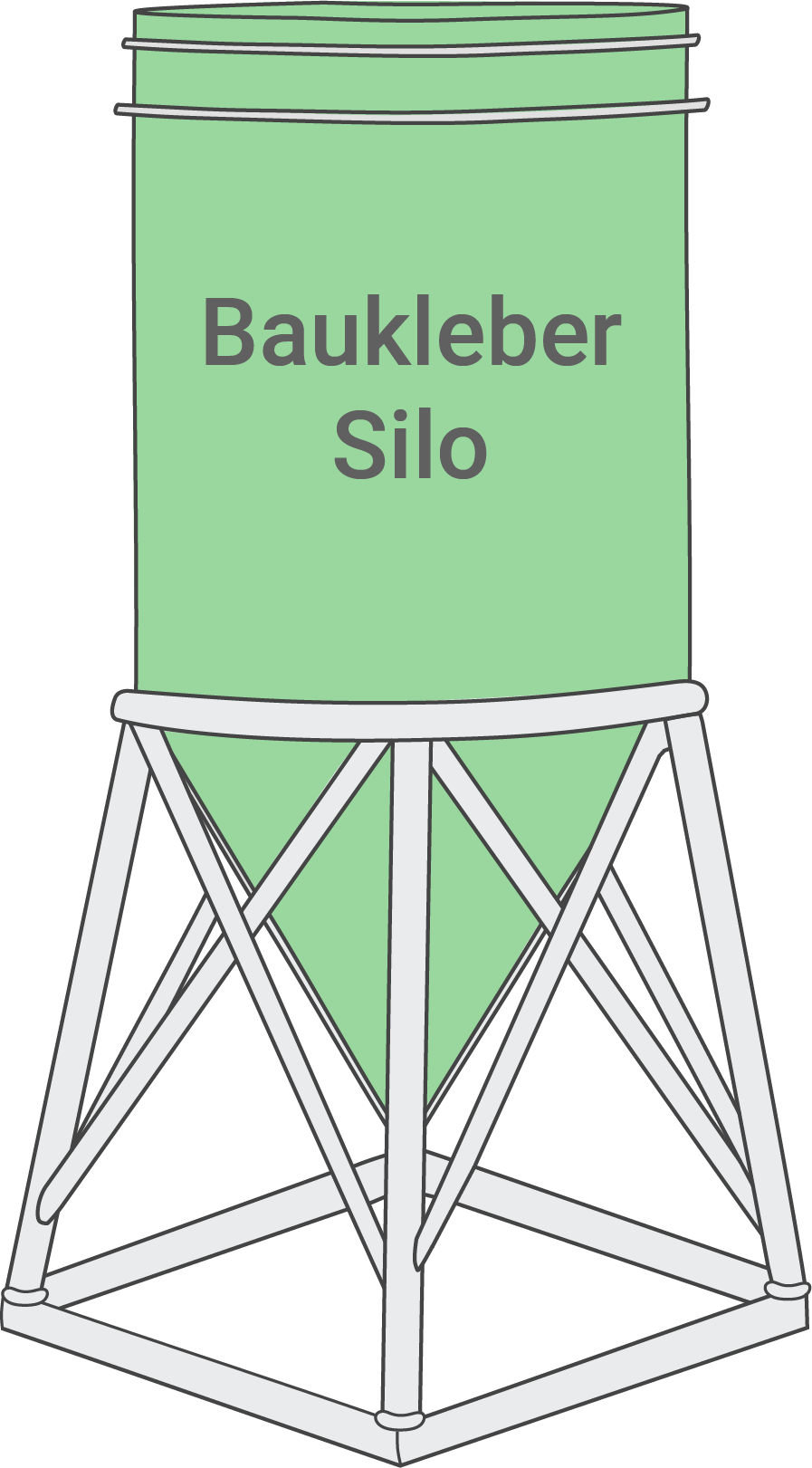
(Abbildung nicht maßstäblich)
a)
Das Silo an der Schule hat die folgenden Maße:
Gesamthöhe des zusammengesetzten Körpers:
Höhe des Kreiskegels:
Durchmesser der Grundfläche: Berechne das Fassungsvermögen dieses Silos.
Berechne das Fassungsvermögen dieses Silos.
Gesamthöhe des zusammengesetzten Körpers:
Höhe des Kreiskegels:
Durchmesser der Grundfläche:
b)
Es gibt weitere Silos für Baukleber mit einem Fassungsvermögen von  oder
oder  Die Dichte des Bauklebers beträgt
Die Dichte des Bauklebers beträgt 
- Ein leeres Silo mit einem Fassungsvermögen von
hat eine Masse von
Gib die Gesamtmasse des gefüllten Silos an. - Auf einer anderen Baustelle müssen auf einer Fläche von
Dämmplatten angebracht werden. Für einen Quadratmeter benötigt man
Baukleber.
Entscheide und begründe rechnerisch, welches Silo geliefert werden sollte.
Für Aufgabe 5 erreichbare BE: 6
Lösung 1
a)
Gesamtpreis berechnen
 Prozentualen Anteil des Notebooks berechnen
Prozentualen Anteil des Notebooks berechnen

Lösungsweg über den Dreisatz

Lösungsweg über die Verhältnisgleichung
![\(\begin{array}[t]{rll}
\dfrac{x}{919\,€}&=& \dfrac{100\,\%}{1\,060,30\,€}&\quad \scriptsize \mid\;\cdot 919\,€ \\[5pt]
x&=& \dfrac{100\,\%}{1\,060,30\,€}\cdot 919\,€& \\[5pt]
x&\approx& \underline{\underline{ 86,7\,\%}}
\end{array}\)](https://www.schullv.de/resources/formulas/25cbc2ba66c8dd5281770f6b32157fc7fc0fa6007dd10020b919a7684c88c55c_light.svg)
Lösungsweg über die Prozentformel
![\(\begin{array}[t]{rll}
p\,\%&=&\dfrac{W\cdot 100}{G}\,\% \\[5pt]
p\,\%&=&\dfrac{919\,€ \cdot 100}{1\,060,30\,€}\,\% \\[5pt]
p\,\%&\approx& \underline{\underline{ 86,7\,\%}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d1b5b2c32577d5b148a241e0cfe18a700c0705cc8f8375dab60055409108c88c_light.svg)
Lösungsweg über den Dezimalbruch

Der prozentuale Anteil des Notebooks beträgt etwa
b)
Auch hier kann die Lösung über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.
Beispielhafter Lösungsweg über den Dezimalbruch
Der Prozentsatz beträgt 
 Franka muss an diesem Tag
Franka muss an diesem Tag  bezahlen.
bezahlen.
c)
Zunächst werden die Zinsen für ein Jahr benötigt. Diese können ebenfalls über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.
Beispielhafter Lösungsweg über den Dezimalbruch
 Damit können die Zinsen für 27 Tage berechnen werden.
Ein Jahr besteht bei Tageszinsen aus 360 Tagen.
Daraus folgt:
Damit können die Zinsen für 27 Tage berechnen werden.
Ein Jahr besteht bei Tageszinsen aus 360 Tagen.
Daraus folgt:  Franka muss
Franka muss  Zinsen bezahlen.
Zinsen bezahlen.
Lösung 2
a)
b)
c)
Da der Graph der Funktion  eine Normalparabel ist und der Scheitelpunkt bereits gegeben ist, kann dieser Graph direkt eingezeichnet werden.
Für den Graph der Funktion
eine Normalparabel ist und der Scheitelpunkt bereits gegeben ist, kann dieser Graph direkt eingezeichnet werden.
Für den Graph der Funktion  müssen zunächst die Koordinaten des Scheitelpunkts
müssen zunächst die Koordinaten des Scheitelpunkts  berechnet werden:
berechnet werden:
 Anhand der Nullstellen
Anhand der Nullstellen  und
und  und dem Scheitelpunkt
und dem Scheitelpunkt  erkennt man, dass es sich bei dem Graph der Funktion
erkennt man, dass es sich bei dem Graph der Funktion  auch um eine Normalparabel handelt. Mit diesen Infos kann auch dieser Graph gezeichnet werden:
auch um eine Normalparabel handelt. Mit diesen Infos kann auch dieser Graph gezeichnet werden:
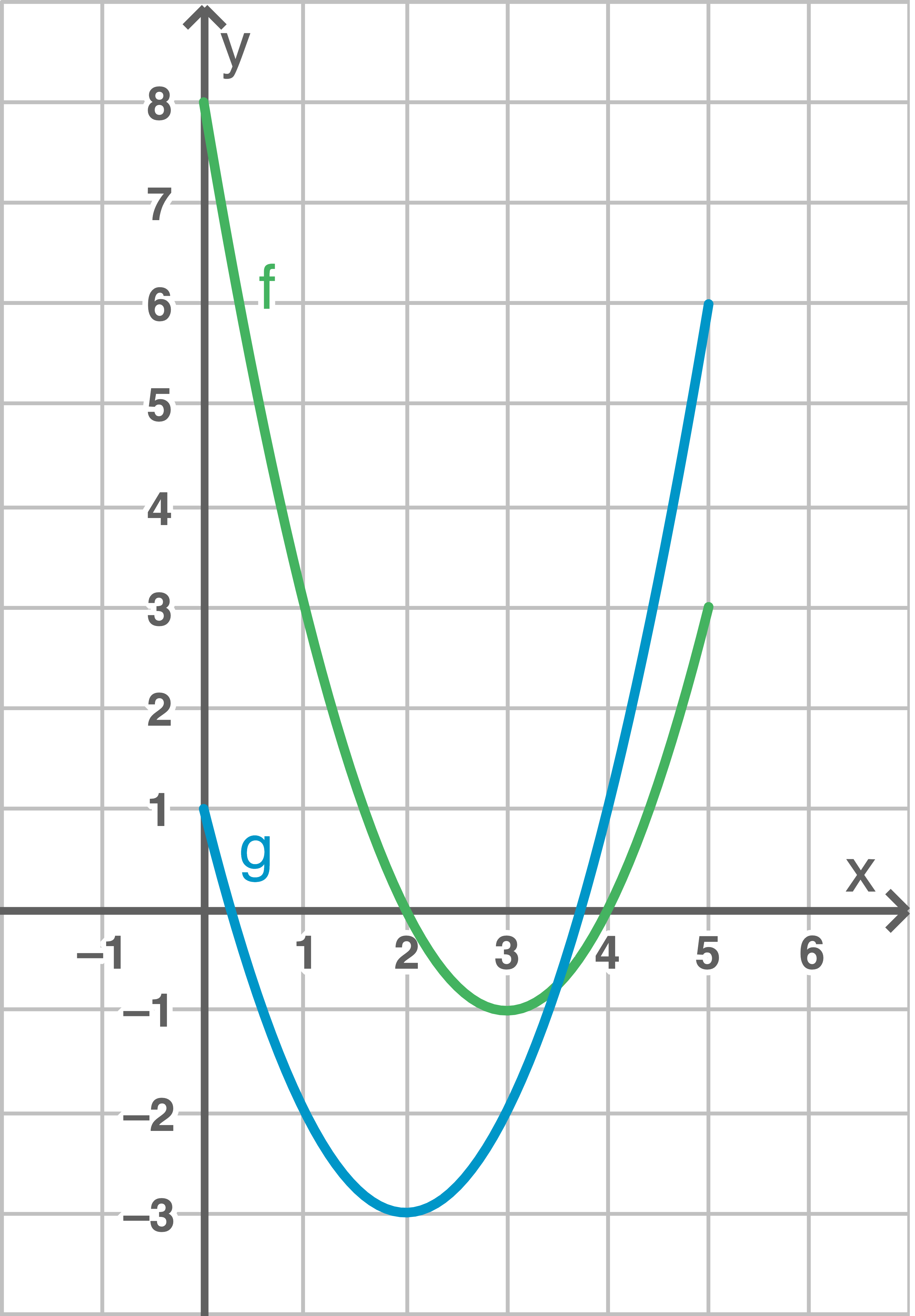

Lösung 3
a)
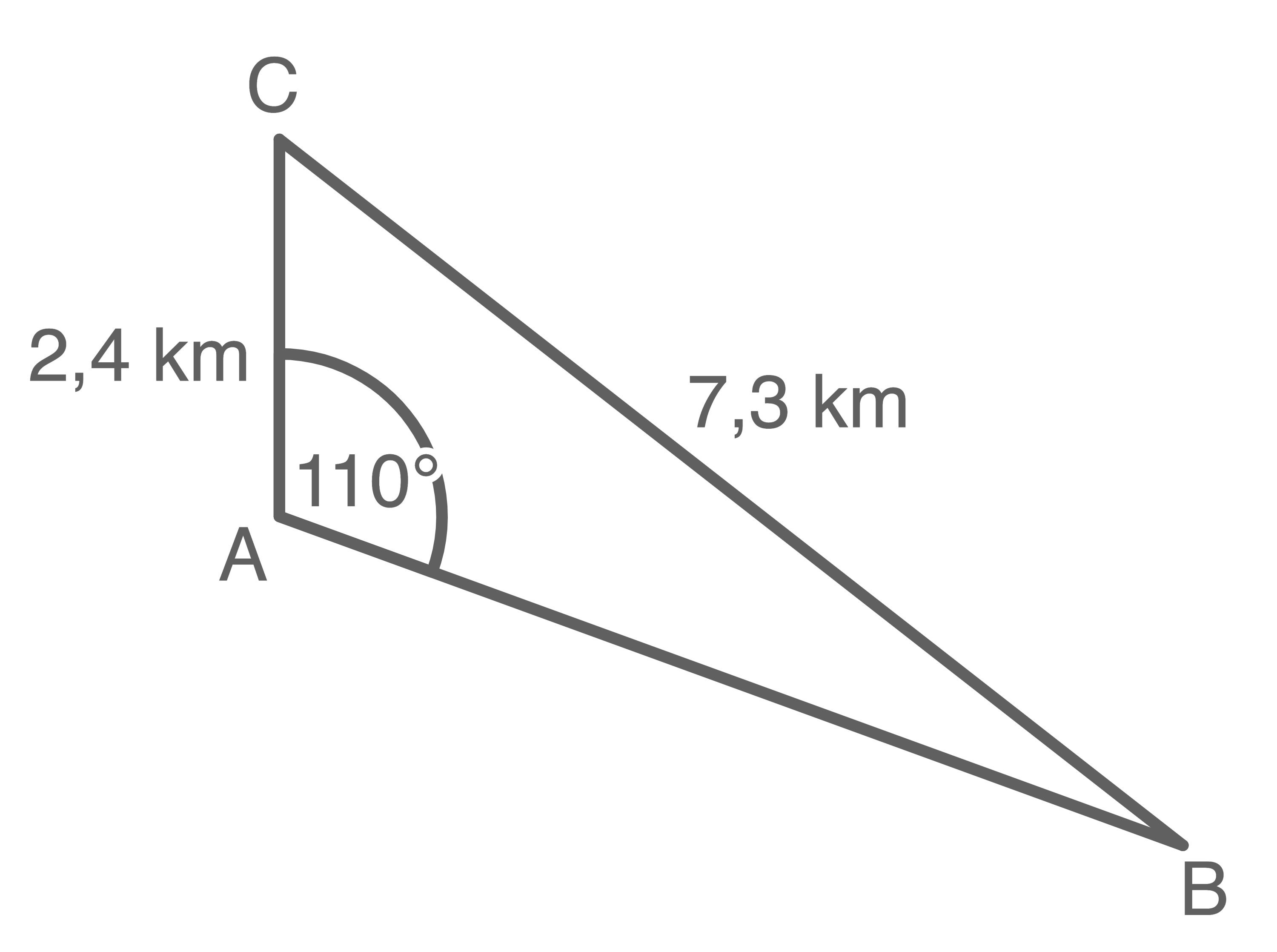
b)
| Originallänge | Bildlänge im Maßstab 1:100 000 |
|---|---|
- Strecke
zeichnen.
- Winkel
in Punkt
abtragen.
- Kreisbogen mit dem Radius
um Punkt
zeichnen.
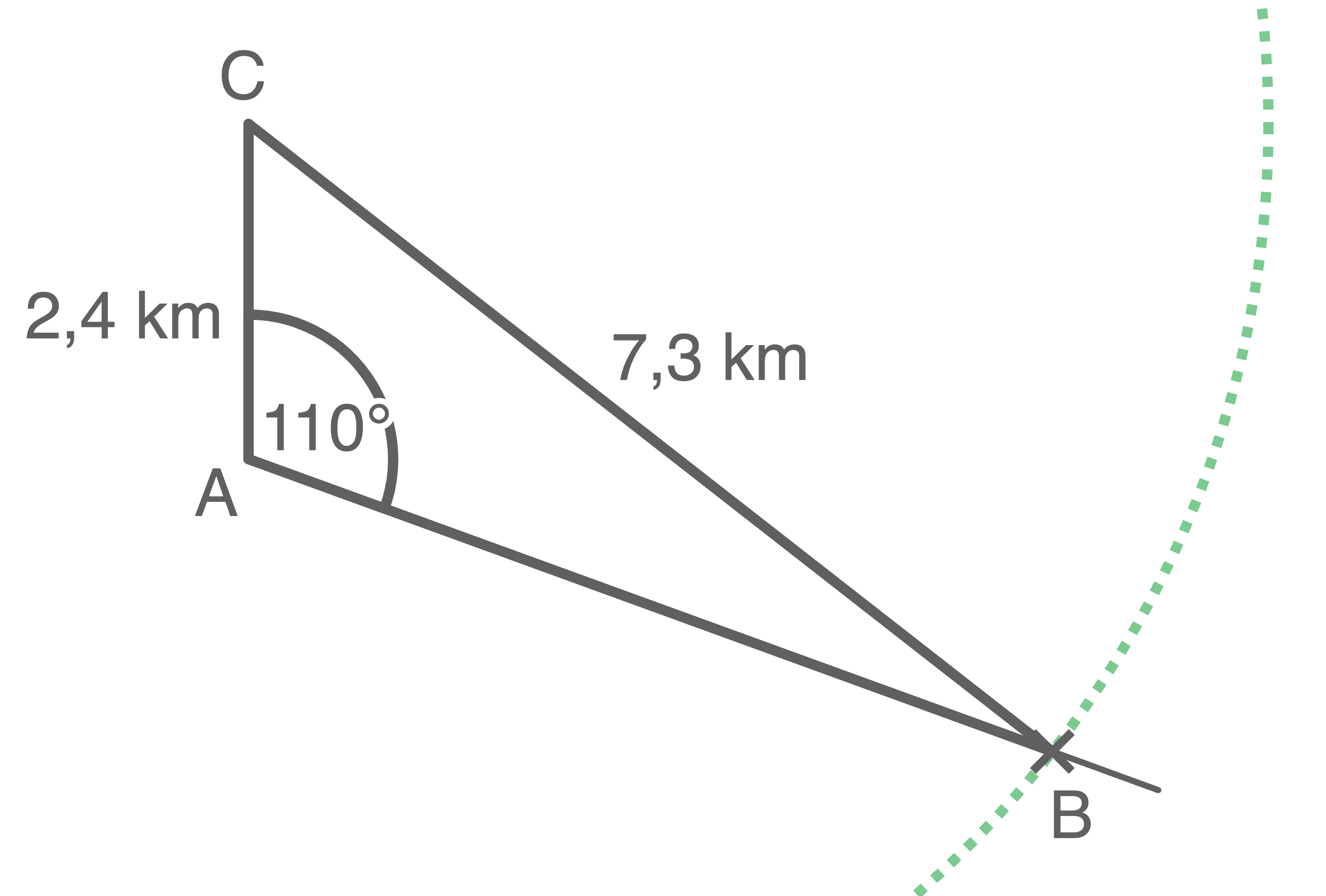
c)
Lösung 4
a)
Wahrscheinlichkeiten angeben

b)
c)
Für die Wahrscheinlichkeiten der Ergebnisse gilt:

![\(\begin{array}[t]{rll}
=&\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{18}+\dfrac{1}{18} \\[5pt]
=&\underline{\underline{ \dfrac{11}{18}}}
\end{array}\)](https://www.schullv.de/resources/formulas/1ca9ca7f40d05b7c90bfd45dd2e872ed10cecdecddf9caf45c33d8d2e7e47971_light.svg) Die Wahrscheinlichkeit, dass Lena zwei Kugeln mit verschiedenen Farben zieht, beträgt
Die Wahrscheinlichkeit, dass Lena zwei Kugeln mit verschiedenen Farben zieht, beträgt 
Lösung 5
a)
b)
Gesamtmasse des gefüllten Silos angeben
Masse des Klebers berechnen
![\(\begin{array}[t]{rll}
\rho&=& \dfrac{m}{V}&\quad \scriptsize \mid\;\cdot V \\[5pt]
\rho\cdot V&=& m\\[5pt]
m&=& \rho\cdot V\\[5pt]
m&=& 1\,500 \frac{\text{kg}}{\text{m}^3}\cdot 18 \,\text{m}^3\\[5pt]
m&=& 27\,000\,\text{kg}\\[5pt]
m&=& 27\,\text{t}
\end{array}\)](https://www.schullv.de/resources/formulas/8a4f255d98b85d453679095d5a1f1bd5a4833ce644f76687c4793dd76bac33fb_light.svg) Gesamtmasse berechnen
Gesamtmasse berechnen
 Die Gesamtmasse des gefüllten Silos beträgt
Die Gesamtmasse des gefüllten Silos beträgt  Welches Silo sollte geliefert werden?
Bedarf an Baukleber in Kilogramm berechnen
Welches Silo sollte geliefert werden?
Bedarf an Baukleber in Kilogramm berechnen
 Bedarf an Baukleber in Kubikzentimeter berechnen
Bedarf an Baukleber in Kubikzentimeter berechnen
![\(\begin{array}[t]{rll}
\rho&=&\dfrac{m}{V} &\quad \scriptsize \mid\;\cdot V \\[5pt]
\rho\cdot V&=&m &\quad \scriptsize \mid\;:\rho \\[5pt]
V&=&\dfrac{m}{\rho} \\[5pt]
V&=&\dfrac{17\,700\,\text{kg}}{1\,500\frac{\text{kg}}{\text{m}^3}} \\[5pt]
V&=&11,8\,\text{m}^3
\end{array}\)](https://www.schullv.de/resources/formulas/e97ce4a4e47819478e4499afdf758e91fc34d1d9be5c714d71b218596da640cb_light.svg) Da
Da  Kleber benötigt werden, sollte ein
Kleber benötigt werden, sollte ein  -Silo geliefert werden.
-Silo geliefert werden.