Teil B – Pflichtaufgaben
Aufgabe 1
Die Mehrwertsteuer ist eine in Deutschland und anderen Ländern für alle Güter und Dienstleistungen zu zahlende Steuer.
Die Tabelle zeigt den jeweils gültigen Mehrwertsteuersatz für ausgewählte Länder im Jahr 2016.
| Land | Mehrwertsteuersatz |
|---|---|
| Dänemark | |
| Deutschland | |
| Luxemburg | |
| Ungarn | |
| Niederlande |
a)
Der Nettopreis einer Uhr beträgt 
Berechne den Bruttopreis dieser Uhr in Deutschland.
Berechne den Bruttopreis dieser Uhr in Deutschland.
b)
Eine Jeans kann man in Ungarn zu einem Bruttopreis von  im Laden kaufen.
im Laden kaufen.
Berechne den Nettopreis dieser Jeans.
Berechne den Nettopreis dieser Jeans.
c)
Der Nettopreis einer Kamera beträgt  Diese wird in den Niederlanden für einen Bruttopreis von
Diese wird in den Niederlanden für einen Bruttopreis von  verkauft.
verkauft.
Ermittle den Mehrwertsteuersatz für die Niederlande.
Ermittle den Mehrwertsteuersatz für die Niederlande.
Für Aufgabe 1 erreichbare BE: 6
Aufgabe 2
Aus einem quadratischen Blatt Papier mit der Seitenlänge  wird durch Falten und Schneiden ein Stern mit fünf Spitzen hergestellt.
Der Stern besteht aus zehn zueinander kongruenten Dreiecken (siehe Abbildungen).
wird durch Falten und Schneiden ein Stern mit fünf Spitzen hergestellt.
Der Stern besteht aus zehn zueinander kongruenten Dreiecken (siehe Abbildungen).

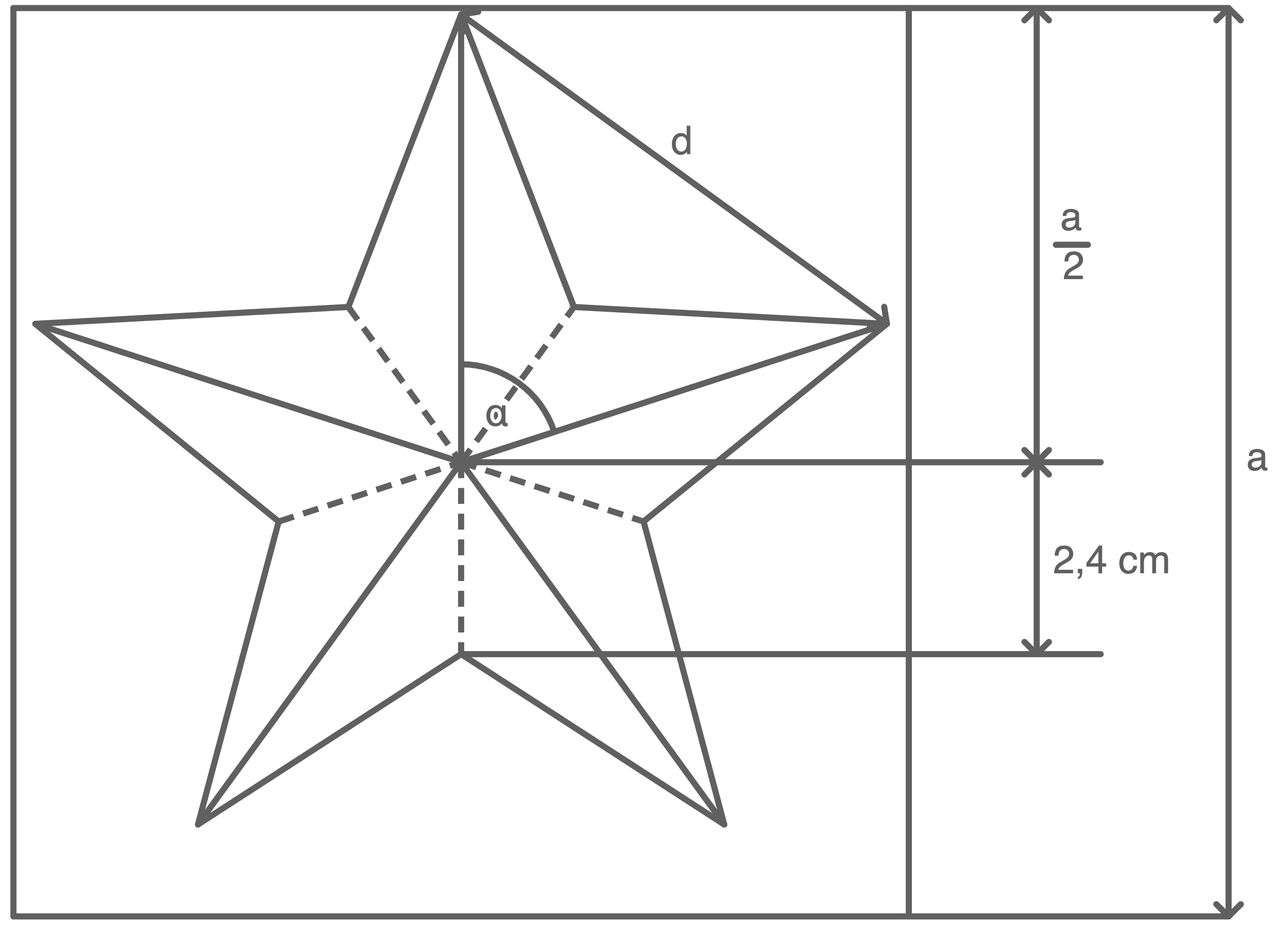
Abbildung (nicht maßstäblich)
a)
Berechne den Abstand 
b)
Berechne den Flächeninhalt des Sterns.
c)
Berechne den Papierabfall bei der Herstellung eines Sterns in Prozent.
Für Aufgabe 2 erreichbare BE: 7
Aufgabe 3
a)
Gegeben ist der folgende Term.
 Löse die Klammern auf und fasse den Term so weit wie möglich zusammen.
Löse die Klammern auf und fasse den Term so weit wie möglich zusammen.
b)
Löse die quadratische Gleichung und führe die Probe durch.

c)
Gegeben ist eine weitere quadratische Gleichung 
Gib den Wert für so an, dass die Gleichung genau eine Lösung hat.
so an, dass die Gleichung genau eine Lösung hat.
Gib den Wert für
Für Aufgabe 3 erreichbare BE: 6
Aufgabe 4
Anna und Bea spielen mit zwei unterschiedlichen Würfeln gegeneinander.
Jede Seitenfläche eines Würfels hat die gleiche Wahrscheinlichkeit gewürfelt zu werden.
Auf jeder Seitenfläche ist eine Zahl abgebildet (siehe Würfelnetze).
Dieses Würfelspiel ist ein zweistufiges Zufallsexperiment.
Jede Seitenfläche eines Würfels hat die gleiche Wahrscheinlichkeit gewürfelt zu werden.
Auf jeder Seitenfläche ist eine Zahl abgebildet (siehe Würfelnetze).
Annas Würfel


Beas Würfel

Zuerst würfelt Anna einmal danach Bea einmal. Es interessiert die jeweils oben liegende Zahl.

Dieses Würfelspiel ist ein zweistufiges Zufallsexperiment.
a)
Zeichne für dieses Zufallsexperiment ein Baumdiagramm und beschrifte alle Pfade mit den entsprechenden Wahrscheinlichkeiten.
b)
Gib die Ergebnismenge des Zufallsexperiments an.
c)
Es gewinnt diejenige, die die größere Zahl würfelt.
Ermittle die Wahrscheinlichkeit für das Ereignis „Anna gewinnt gegen Bea“.
Ermittle die Wahrscheinlichkeit für das Ereignis „Anna gewinnt gegen Bea“.
Für Aufgabe 4 erreichbare BE: 6
Aufgabe 5
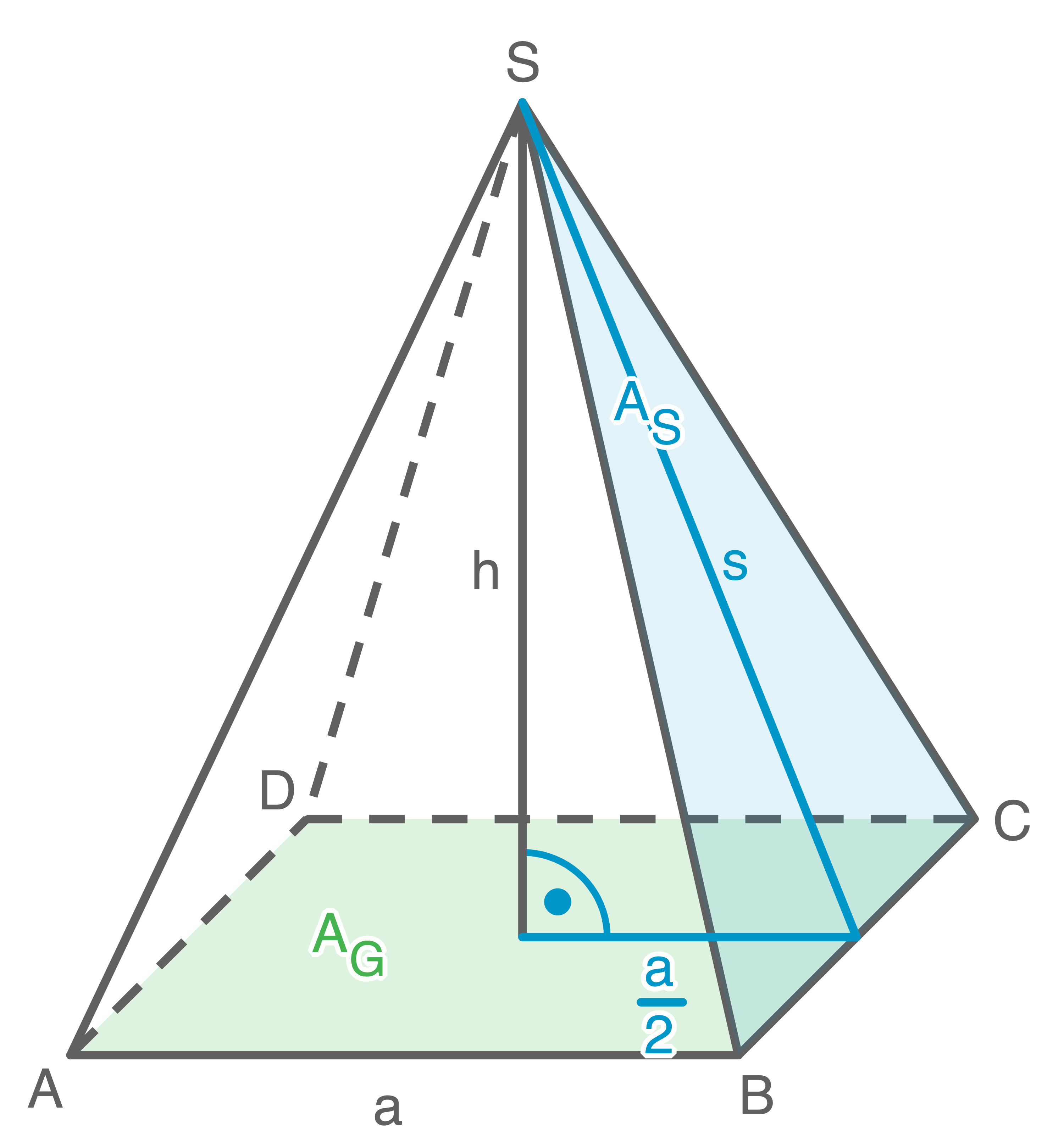
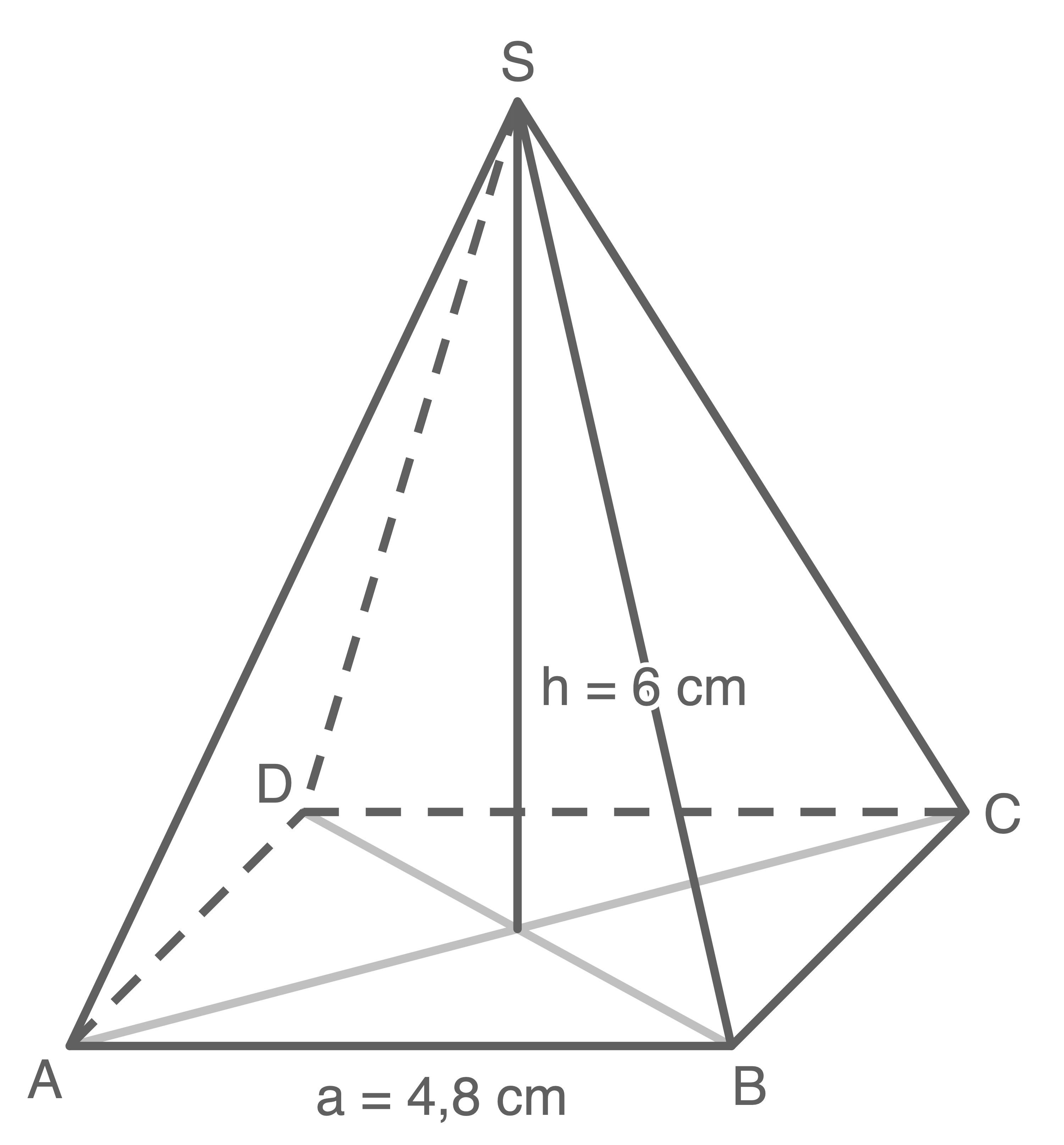
Gegeben ist eine quadratische Pyramide  mit der Grundkantenlänge
mit der Grundkantenlänge  und der Höhe
und der Höhe 
a)
Zeichne das Schrägbild der Pyramide  im Maßstab 2:1.
im Maßstab 2:1.
b)
Berechne den Oberflächeninhalt der Pyramide.
Für Aufgabe 5 erreichbare BE: 6
Lösung 1
a)
Lösungsweg über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 78\,€\\[5pt]
1\,\% & \mathrel{\widehat{=}}& \dfrac{78}{100}\,€\\[5pt]
119\,\% & \mathrel{\widehat{=}}& \dfrac{78}{100}\cdot 119\,€
\end{array}\)](https://www.schullv.de/resources/formulas/21e578263f7c0359ca73a0ad8ab0647167b13475130247a7de2145f449a98526_light.svg)





Lösungsweg über die Verhältnisgleichung
![\(\begin{array}[t]{rll}
\dfrac{x}{119\,\%}&=&\dfrac{78\,€}{100\,\%} &\quad \scriptsize \mid\;\cdot 119\,\% \\[5pt]
x&=&\dfrac{78\,€}{100\,\%}\cdot 119\,\% \\[5pt]
x&=&\underline{\underline{ 92,82\,€}}
\end{array}\)](https://www.schullv.de/resources/formulas/d2bfdf51262fa0a9300e16f231c9f0ea1047e516ba6cd942eaaf9eeabd2bd168_light.svg)
Lösungsweg über die Prozentformel
![\(\begin{array}[t]{rll}
W&=&\dfrac{G\cdot p}{100} \\[5pt]
W&=&\dfrac{78\,€\cdot 119}{100} \\[5pt]
W&=&\underline{\underline{ 92,82\,€}}
\end{array}\)](https://www.schullv.de/resources/formulas/566722c8e3af3d501feecf431dd0e1e0ace3d8295219486893d58cefd14e92b6_light.svg)
Lösungsweg über den Dezimalbruch

Der Bruttopreis der Uhr beträgt
b)
Der Nettopreis der Jeans kann wieder über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch berechnet werden.
Beispielhafter Lösungsweg über die Prozentformel
![\(\begin{array}[t]{rll}
G&=&\dfrac{W\cdot 100}{p} \\[5pt]
G&=&\dfrac{59\,€ \cdot 100}{127} \\[5pt]
G&\approx&\underline{\underline{ 46,46\,€}}
\end{array}\)](https://www.schullv.de/resources/formulas/125c4cdf2f4cf7b627e19b0fa81b075f8a3ac48084a35088f3bddd7c6bc9845d_light.svg) Der Nettopreis der Jeans beträgt
Der Nettopreis der Jeans beträgt 
c)
Auch hier kann der Mehrwertsteuersatz über den Dreisatz, die Verhältnisgleichung, die Prozentformel oder den Dezimalbruch ermittelt werden.
Beispielhafter Lösungsweg über den Dreisatz




![\(\begin{array}{rcl}
137\,€ & \mathrel{\widehat{=}}& 100\,\%\\[5pt]
1\,€ & \mathrel{\widehat{=}}& \dfrac{100}{137}\,\%\\[5pt]
165,77\,€ & \mathrel{\widehat{=}}& \dfrac{100}{137}\cdot 165,77\,\%\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/43249829c7ea6e61d9827aa907b22b48c6303a341687bd1b546515f1a9a0f822_light.svg)




 Daraus folgt:
Daraus folgt:  Der Mehrwertsteuersatz der Niederlande beträgt
Der Mehrwertsteuersatz der Niederlande beträgt 
Lösung 2
a)
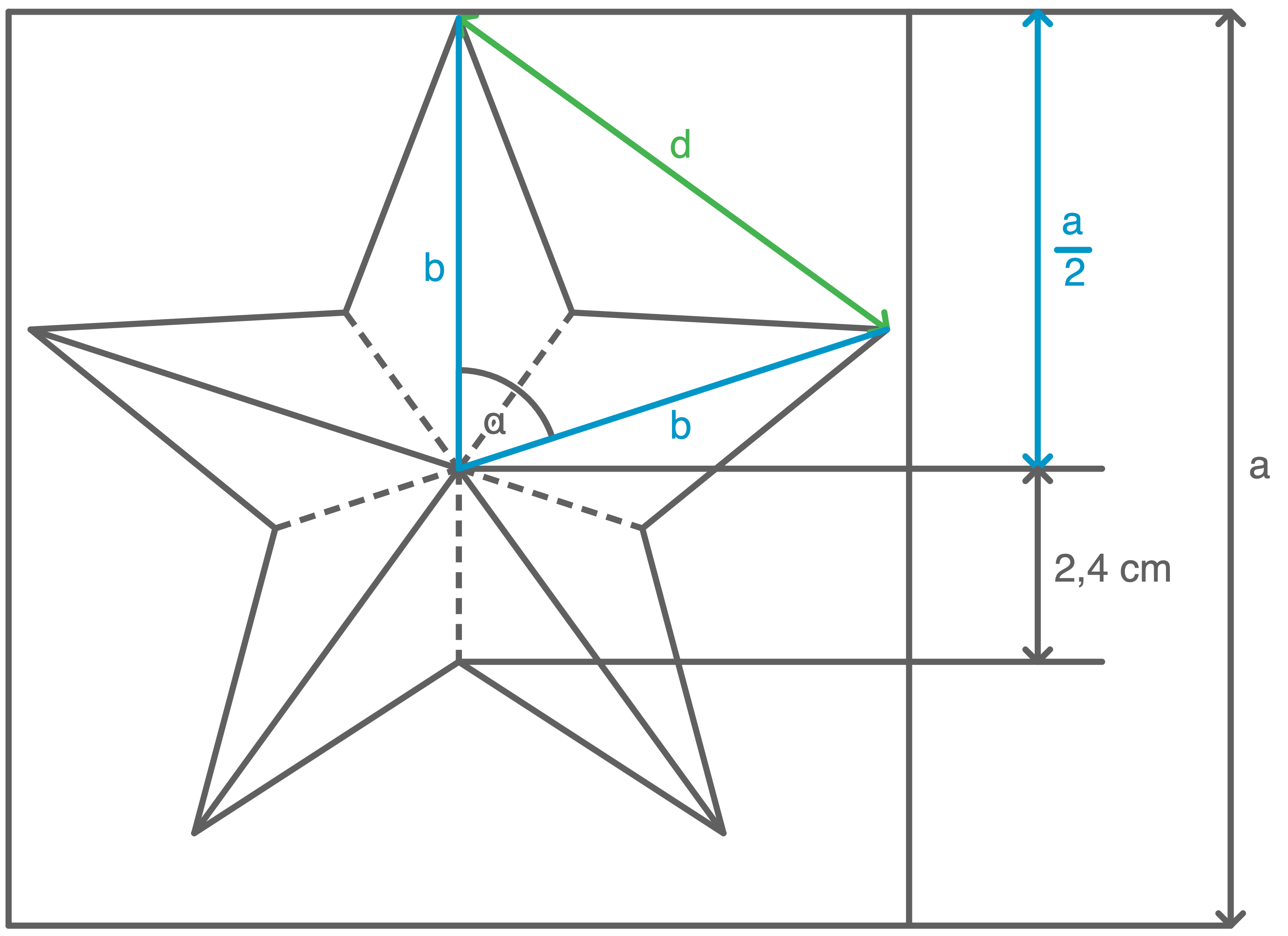
b)
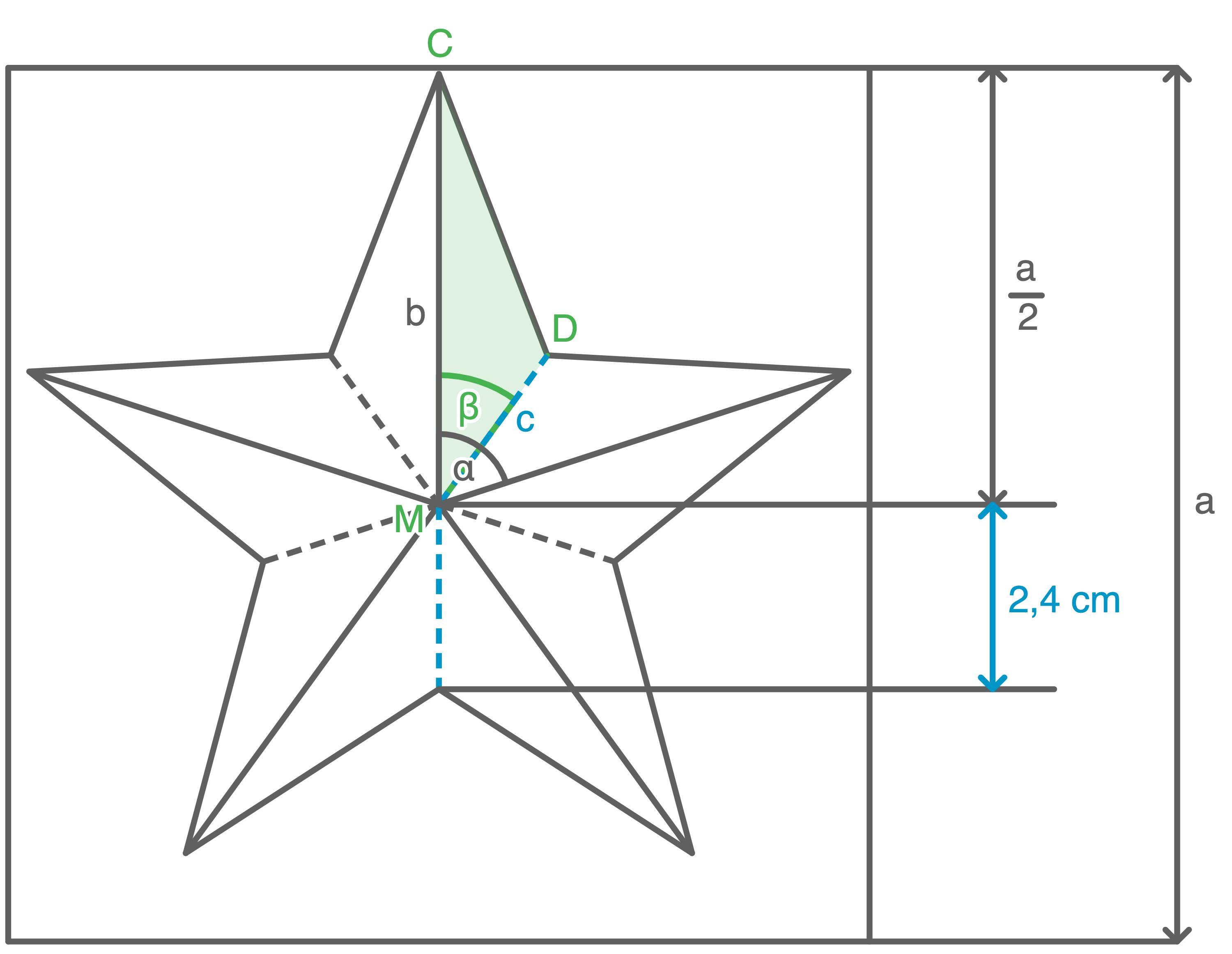
c)
Der Flächeninhalt des Papiers beträgt  Der Papierabfall beträgt
Der Papierabfall beträgt  Daraus folgt:
Daraus folgt:
 Der Papierabfall bei der Herstellung eines Sterns beträgt etwa
Der Papierabfall bei der Herstellung eines Sterns beträgt etwa 
Lösung 3
a)
b)
Quadratische Gleichung lösen
![\(\begin{array}[t]{rll}
2x^2+6x-5,5&=&8 & \quad \scriptsize \mid\;-8 \\[5pt]
2x^2+6x-13,5&=&0 & \quad \scriptsize \mid\;:2 \\[5pt]
x^2+3x-6,75&=&0 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/0a07d4e4d888d05f59a39325dac5d30203da29da65061b92eaff5556e827468c_light.svg)
![\(\begin{array}[t]{rll}
x_{1,2}&=&-\dfrac{3}{2}\pm\sqrt{\left(\dfrac{3}{2}\right)^2-(-6,75)} \\[5pt]
x_{1,2}&=&-1,5\pm\sqrt{\dfrac{9}{4}+6,75} \\[5pt]
x_{1,2}&=&-1,5\pm\sqrt{9} \\[5pt]
x_{1}&=&-1,5+3=\underline{\underline{ 1,5}}\\[5pt]
x_{2}&=&-1,5-3=\underline{\underline{ -4,5}}
\end{array}\)](https://www.schullv.de/resources/formulas/4f799078419bf115c4daba06da955cdee7e05cd11f13f0c068d6e94f1fa2ebd3_light.svg) Probe für
Probe für  durchführen
durchführen
![\(\begin{array}[t]{rll}
2x^2+6x-5,5&=& 8\\[5pt]
2\cdot 1,5^2+6\cdot 1,5-5,5&=& 8&\quad \scriptsize ? \\[5pt]
8&=& 8&\quad \scriptsize \text{wahr} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/86ac20b6a1a6b061d7acecb819129793aaf5f164550617353b1a69e7c8f540e2_light.svg) Probe für
Probe für  durchführen
durchführen
![\(\begin{array}[t]{rll}
2x^2+6x-5,5&=& 8\\[5pt]
2\cdot (-4,5)^2+6\cdot (-4,5)-5,5&=& 8&\quad \scriptsize ? \\[5pt]
8&=& 8&\quad \scriptsize \text{wahr} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2258c36409f6c013ffdca5916ed9dee330b5edb00d608dbdd718ff5f3ba42814_light.svg) Die quadratische Gleichung hat die Lösungen
Die quadratische Gleichung hat die Lösungen  und
und 
c)
Lösung 4
a)
Wahrscheinlichkeiten bei Annas Würfel:
Wahrscheinlichkeiten bei Beas Würfel:
Mit diesen Wahrscheinlichkeiten kann das Baumdiagramm gezeichnet werden:
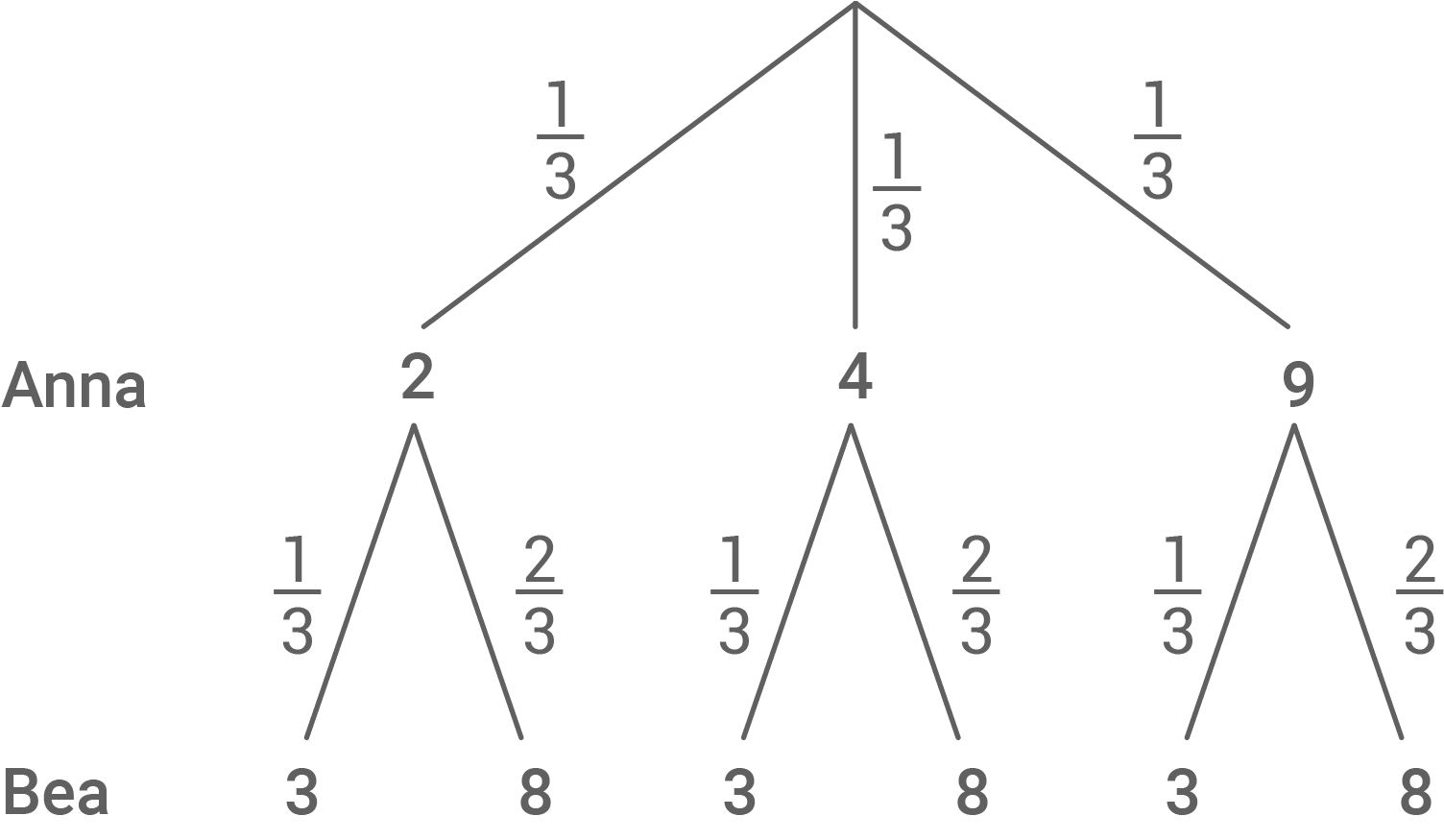
b)
c)
Anna gewinnt bei folgenden Ergebnissen:  und
und 
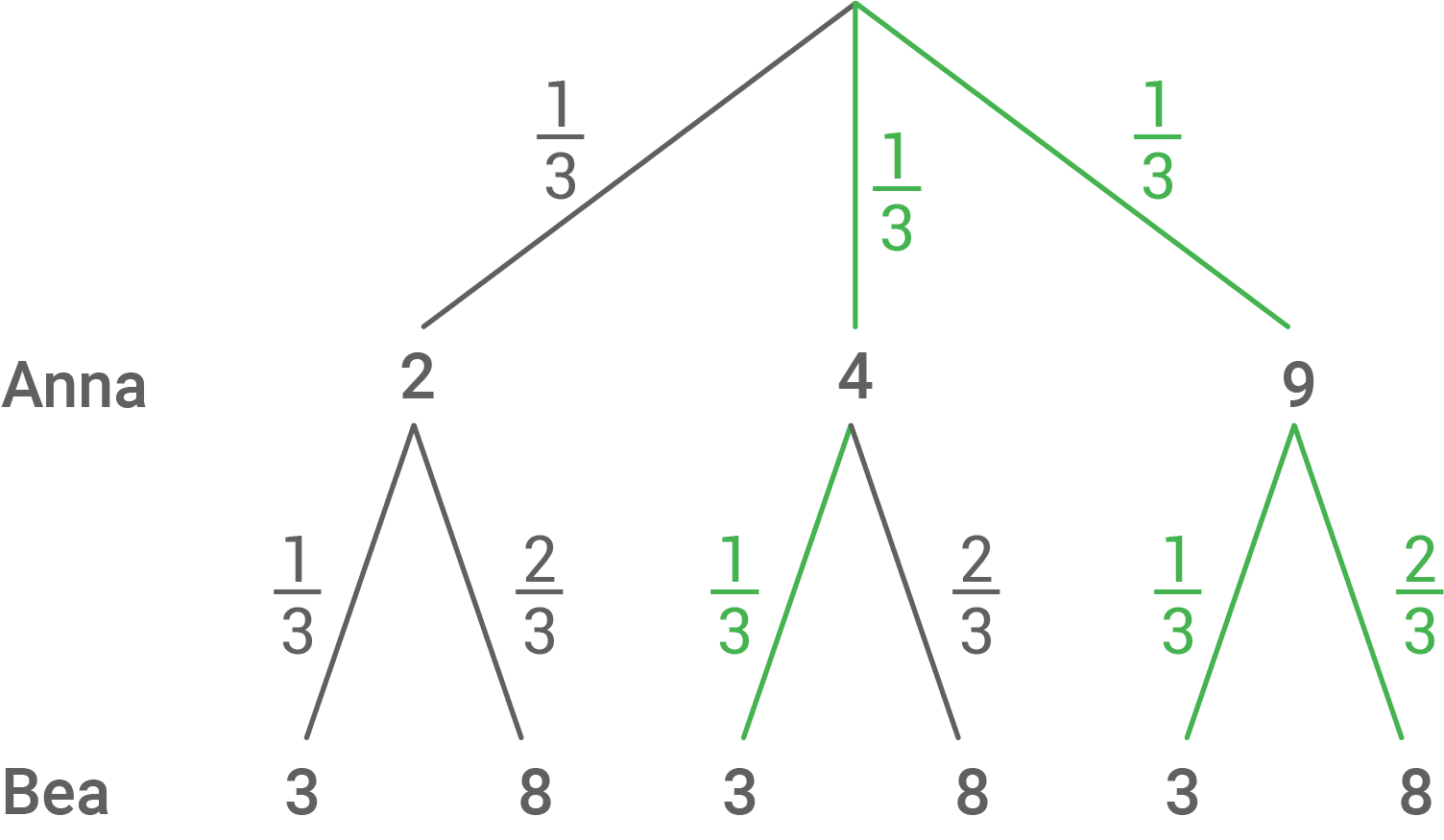 Daraus folgt:
Daraus folgt:
![\(\begin{array}[t]{lll}
P(4;3)+P(9;3)+P(9;8) \\[5pt]
=\dfrac{1}{3}\cdot \dfrac{1}{3}+\dfrac{1}{3}\cdot \dfrac{1}{3}+\dfrac{1}{3}\cdot \dfrac{2}{3} \\[5pt]
=\underline{\underline{ \dfrac{4}{9}}}
\approx \underline{\underline{0,444}}
=\underline{\underline{ 44,4\,\%}}
\end{array}\)](https://www.schullv.de/resources/formulas/cc2cb5ff5ec5ff71191bc21c5761726bbc451086d2bc6d1b475d608c62dcfb73_light.svg) Die Wahrscheinlichkeit, dass Anna gegen Bea gewinnt, beträgt etwa
Die Wahrscheinlichkeit, dass Anna gegen Bea gewinnt, beträgt etwa 

Lösung 5
a)
| Originallänge | Bildlänge im Maßstab 2:1 |
|---|---|
b)