Teil B – Pflichtaufgaben

Aufgabe 1

Paul hat im Internet die folgende Tabelle für den durchschnittlichen Mietpreis in verschiedenen Städten gefunden.

Stadt	Mietpreis pro Quadratmeter
Berlin	$11,97\,€$
Dresden	$5,46\,€$
Leipzig	$5,39\,€$
München	$17,71\,€$
Stuttgart	$13,70\,€$

Alle folgenden Berechnungen beziehen sich auf diese durchschnittlichen Mietpreise.

Gib an, welchen Betrag man in Dresden für eine $45,0 \,\text{m}^2$ große Wohnung an Miete bezahlt.

Berechne, um wie viel Prozent der Mietpreis pro Quadratmeter in München höher liegt als in Dresden.

Paul erhielt in Leipzig ein Angebot für eine $42,0\,\text{m}^2$ große Wohnung zur Miete. Die Wohnungskosten setzen sich aus der Miete und $75,00\,\,€$ Nebenkosten zusammen. Er möchte für die Wohnungskosten maximal $30\,\%$ seines Einkommens ausgeben. Sein Einkommen beträgt $870,00\,\,€.$

Entscheide und begründe rechnerisch, ob Paul diese Wohnung mieten kann.

Für Aufgabe 1 erreichbare BE: 5

Aufgabe 2

Gegeben ist die Funktion $f$ mit der Gleichung $y=f(x)=2\cdot \sin x.$

Skizziere den Graphen der Funktion $f$ mindestens im Intervall $-\pi \leq x \leq 2\pi$ in ein Koordinatensystem.

Gib den Wertebereich der Funktion $f$ an.

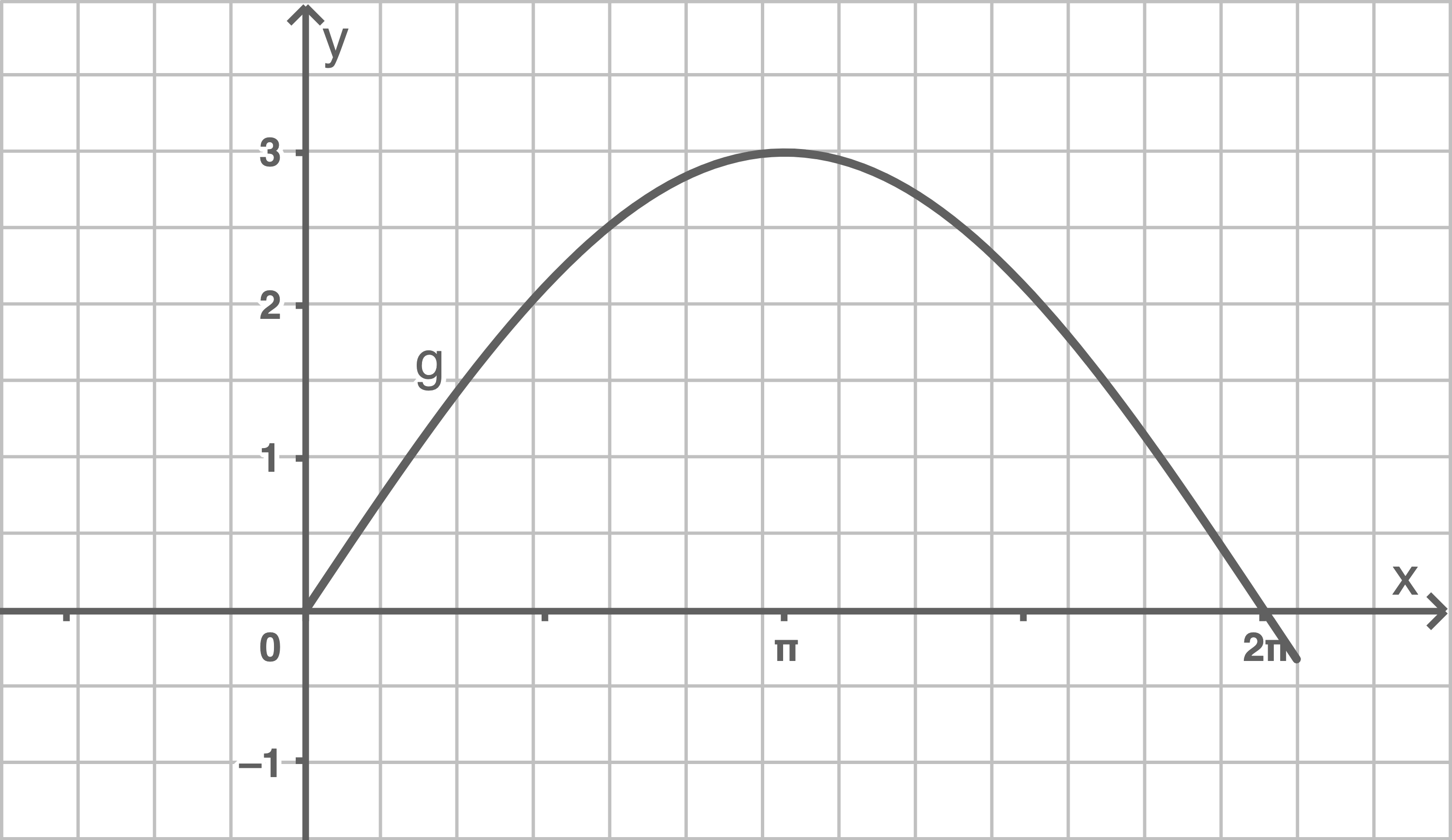
In der folgenden Abbildung ist der Graph einer weiteren Funktion $g$ mit der Gleichung $y=g(x)=a\cdot \,\text{sin}(bx)$ dargestellt.

Gib die Werte für $a$ und $b$ an.

Abbildung

Für Aufgabe 2 erreichbare BE: 5

Aufgabe 3

Der Fußboden einer Bühne hat die Form eines gleichschenkligen Trapezes (siehe Abbildung). Für eine Theatervorstellung wird der Fußboden der Bühne zweifarbig gestaltet.

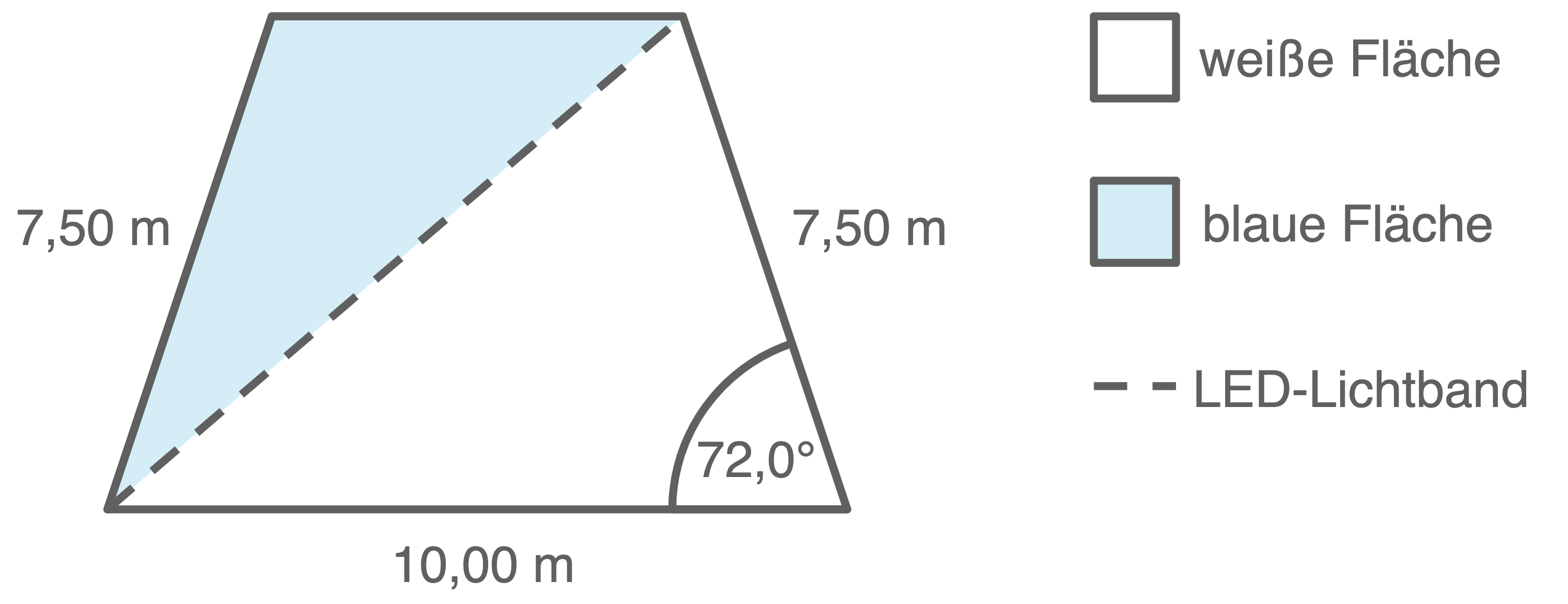
Abbildung (nicht maßstäblich)

Berechne den Flächeninhalt der weißen Fläche.

An der Trennlinie der beiden Farben wird ein LED-Lichtband aufgeklebt.
Berechne die Länge des LED-Lichtbandes.

Berechne den Flächeninhalt der blauen Fläche.

Für Aufgabe 3 erreichbare BE: 7

Aufgabe 4

Andreas und Paula spielen Dart mit dem Ziel, pro Durchgang möglichst viele Punkte zu werfen. Sie notieren ihre Punkte der Reihe nach in einer Tabelle.

Andreas	Paula
43, 77, 96, 26, 123, 57, 76, 95, 139, 98, 38, 60, 85, 101, 41	93, 57, 128, 140, 100, 94, 41, 58, 100, 139, 83, 100, 57, 43, 96

Berechne für Andreas das arithmetische Mittel seiner Punkte.

Gib für Paula den Modalwert ihrer Punkte an.

Für einen Teamwettbewerb werden die Punkte von Andreas und Paula zusammen betrachtet.

Übernimm die Häufigkeitstabelle und vervollständige diese.

Punkte im Bereich	Absolute Häufigkeit	Relative Häufigkeit
von 0 bis 45
von 46 bis 90
von 91 bis 135
von 136 bis 180

Stelle diese relativen Häufigkeiten der Bereiche in einem Kreisdiagramm dar.

Für Aufgabe 4 erreichbare BE: 7

Aufgabe 5

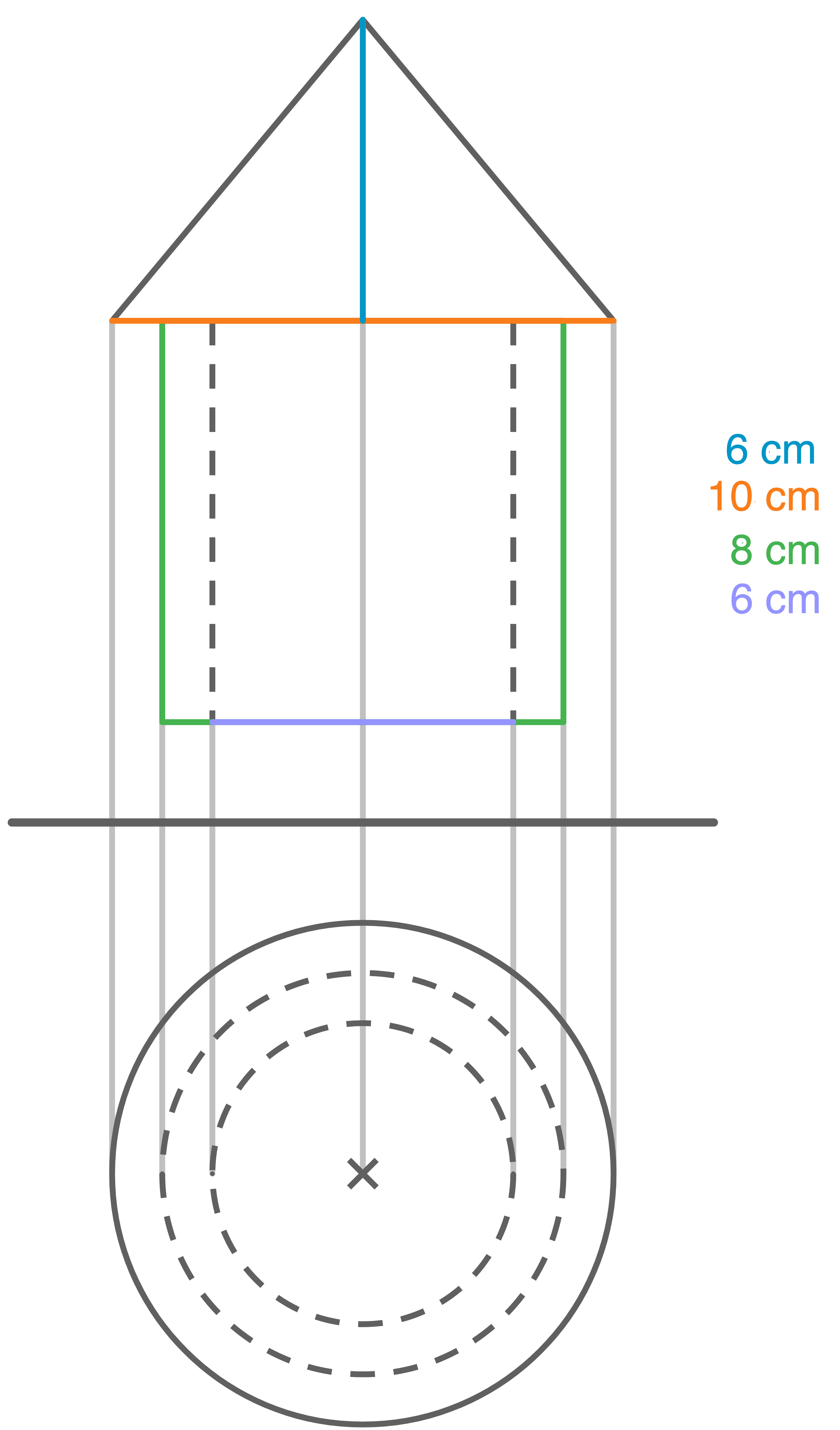
Gegeben sind ein Hohlzylinder und ein Kreiskegel mit den folgenden Maßen.

Hohlzylinder

Höhe: $h=8,0\,\text{cm}$
äußerer Durchmesser: $d_a=8,0\,\text{cm}$
innerer Durchmesser: $d_i=6,0\,\text{cm}$

Kreiskegel

Durchmesser: $d=10,0\,\text{cm}$
Mantellinie: $s=7,8\,\text{cm}$

Berechne das Volumen des Hohlzylinders.

Berechne die Höhe des Kreiskegels.

Beide Körper werden zusammmengesetzt. Die Abbildung zeigt den Grundriss des zusammengesetzten Körpers.

Sachsen Teil B Pflichtaufgaben Kreiskegel

Abbildung (nicht maßstäblich)

Zeichne ein senkrechtes Zweitafelbild des zusammengesetzten Körpers.

Für Aufgabe 5 erreichbare BE: 6

Lösung 1

$45\cdot 5,46\,€=\underline{\underline{ 245,70\,€}}$

In Dresden muss man für eine $45,0\,\text{m}^2$ große Wohnung $245,70\,€$ Miete bezahlen.

Der Unterschied zwischen Dresden und München in Euro beträgt $17,71\,€-5,46\,€=12,25\,€.$
In Prozent kann dieser Unterschied durch unterschiedliche Lösungswege berechnet werden:

Lösungsweg über den Dreisatz

$:5,46$

$\cdot 12,25$ Graue Pfeilform, die eine Kurve darstellt.

$\begin{array}{rcl} 5,46\,€ & \mathrel{\widehat{=}}& 100\,\%\\[5pt] 1,00\,€ & \mathrel{\widehat{=}}& \dfrac{100}{5,46}\,\%\\[5pt] 12,25\,€ & \mathrel{\widehat{=}}& \dfrac{100}{5,46}\cdot 12,25\,\% \end{array}$

$:5,46$

$\cdot 12,25$

$12,25\,€ \mathrel{\widehat{=}}\underline{\underline{ 224,36\,\%}}$

Lösungsweg über die Verhältnisgleichung

$\begin{array}[t]{rll} \dfrac{x}{12,25\,€}&=&\dfrac{100\,\%}{5,46\,€} &\quad \scriptsize \mid\; \cdot 12,25\,€\\[5pt] x&=&\dfrac{100\,\%}{5,46\,€}\cdot 12,25\,€ \\[5pt] x&\approx&\underline{\underline{ 224,36\,\%}} \end{array}$

Lösungsweg über die Prozentformel

$\begin{array}[t]{rll} p\,\%&=&\dfrac{W\cdot 100}{G}\,\% \\[5pt] p\,\%&=&\dfrac{12,25\,€\cdot 100}{5,46\,€}\,\% \\[5pt] p\,\%&\approx&\underline{\underline{ 224,36\,\%}} \end{array}$

Lösungsweg über den Dezimalbruch

$\dfrac{12,25\,€}{5,46\,€}\approx 2,2436=\underline{\underline{ 224,36\,\%}}$

Der Mietpreis pro Quadratmeter in München liegt um etwa $224,36\,\%$ höher als in Dresden.

Die Miete beträgt $42\cdot 5,39\,€=226,38\,€.$

Die Wohnkosten betragen damit $226,38\,€+75,00\,€=301,38\,€.$

Die Wohnkosten, die Paul maximal ausgeben möchte, können mit dem Dreisatz, der Verhältnisgleichung, der Prozentformel oder mit dem Dreisatz berechnet werden.

Beispielhafter Lösungsweg über die Prozentformel

$\begin{array}[t]{rll} W&=& \dfrac{G\cdot p}{100} \\[5pt] W&=& \dfrac{870,00\,€\cdot 30}{100} \\[5pt] W&=& 261,00\,€ \end{array}$

Es gilt: $301,38\,€\gt 261,00\,€$

Paul kann diese Wohnung nicht mieten, da die Wohnkosten die $30\,\%$ seines Einkommens überschreiten.

Lösung 2

$\underline{\underline{ -2\leq y\leq 2}}$

Faktor $a$ angeben

Da der größte Funktionswert $3$ ist und die Funktion nicht an einer der Koordinatenachsen gespiegelt ist, gilt $a=\underline{\underline{3}}.$

Faktor $b$ angeben

Mithilfe der Abbildung können die ersten Nullstellen abgelesen werden: $x_1=0$ und $x_2=2\pi$
Die kleinste Periode beträgt also $p=4\pi.$

Daraus folgt:

$\begin{array}[t]{rll} p&=&\dfrac{2\pi}{b} &\quad \scriptsize \mid\;\cdot b \\[5pt] p\cdot b&=&2\pi &\quad \scriptsize \mid\;:p \\[5pt] b&=&\dfrac{2\pi }{p}\\[5pt] b&=&\dfrac{2\pi }{4\pi}\\[5pt] b&=&\underline{\underline{ 0,5}} \end{array}$

Alternativer Lösungsweg

Durch Spiegelung an der $x$ - und $y$ -Achse entsteht der gleiche Graph wie in der Abbildung. In diesem Fall sind der Faktor $a$ und der Faktor $b$ negativ. Zweite mögliche Lösung: $a=\underline{\underline{ -3}}$ und $a=\underline{\underline{ -0,5}}.$

Lösung 3

Höhe $h$ berechnen

$\begin{array}[t]{rll} \dfrac{h}{b}&=&\sin\beta &\quad \scriptsize \mid\;\cdot b\\[5pt] h&=&\sin\beta\cdot b \\[5pt] h&=&\sin 72^\circ\cdot 7,50\,\text{m} \\[5pt] h&\approx&7,13\,\text{m} \end{array}$

Flächeninhalt berechnen

$\begin{array}[t]{rll} A_{ABC}&=&\dfrac{1}{2}\cdot a\cdot h \\[5pt] A_{ABC}&=&\dfrac{1}{2}\cdot 10,00\,\text{m}\cdot 7,13\,\text{m} \\[5pt] A_{ABC}&=&\underline{\underline{ 35,65\,\text{m}^2}} \end{array}$

Der Flächeninhalt der weißen Fläche beträgt ca. $35,65\,\text{m}^2.$

Kosinussatz anwenden:

$\begin{array}[t]{rll} e^2&=&a^2+b^2-2\cdot a\cdot b\cdot \cos\beta & \scriptsize \mid\;\sqrt{\,\,} \\[5pt] e&=&\sqrt{a^2+b^2-2\cdot a\cdot b\cdot \cos\beta} \\[5pt] e&=&\sqrt{(10^2+7,5^2-2\cdot 10\cdot 7,5\cdot \cos72^\circ}\\[5pt] e&\approx&\underline{\underline{ 10,48}} \end{array}$

Die Länge des LED-Lichtbandes beträgt ca. $10,48\,\text{m}.$

Länge der Strecke $x$ berechnen

Satz des Pythagoras anwenden:

$\begin{array}[t]{rll} x^2+h^2&=&b^2 &\quad \scriptsize \mid\;-h^2 \\[5pt] x^2&=&b^2-h^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt] x&=&\sqrt{b^2-h^2} \\[5pt] x&=&\sqrt{(7,5\,\text{m})^2-(7,13\,\text{m})^2} \\[5pt] x&\approx&2,33\,\text{m} \end{array}$

Länge der Strecke $c$ berechnen

$\begin{array}[t]{rll} c&=& a-x-x \\[5pt] c&=& 10\,\text{m}-2,33\,\text{m}-2,33\,\text{m} \\[5pt] c&=& 5,34\,\text{m} \end{array}$

Flächeninhalt des Trapezes berechnen

$\begin{array}[t]{rll} A_T&=&\dfrac{a+c}{2}\cdot h \\[5pt] A_T&=&\dfrac{10\,\text{m}+ 5,34\,\text{m}}{2}\cdot 7,13\,\text{m} \\[5pt] A_T&\approx& 54,69\,\text{m}^2 \end{array}$

Flächeninhalt der blauen Fläche berechnen

$\begin{array}[t]{rll} A_{ACD}&=&A_T-A_{ABC} \\[5pt] A_{ACD}&=&54,69\,\text{m}^2-35,65\,\text{m}^2 \\[5pt] A_{ACD}&=&\underline{\underline{ 19,04\,\text{m}^2}} \end{array}$

Der Flächeninhalt der blauen Fläche beträgt $19,04\,\text{m}^2.$

Lösung 4

Rechenweg anzeigen

Das arithmetische Mittel von Andreas beträgt $77.$

Der Modalwert ist der Wert, der am häufigsten vorkommt.

Der Modalwert der Punkte von Paula beträgt $\underline{\underline{ 100}}.$

Häufigkeitstabelle übernehmen und vervollständigen

Zur Berechnung der relativen Häufigkeit wird die absolute Häufigkeit durch die Anzahl aller Werte geteilt:

Punkte im Bereich	Absolute Häufigkeit	Relative Häufigkeit
von 0 bis 45	$6$	$\dfrac{6}{30}=0,20=20\,\%$
von 46 bis 90	$9$	$\dfrac{9}{30}=0,30=30\,\%$
von 91 bis 135	$12$	$\dfrac{12}{30}=0,40=40\,\%$
von 136 bis 180	$3$	$\dfrac{3}{30}=0,10=10\,\%$

Relative Häufigkeiten in einem Kreisdiagramm darstellen

Punkte im Bereich	Winkelgröße
von 0 bis 45	$0,20\cdot 360^\circ=72\,\%$
von 46 bis 90	$0,30\cdot 360^\circ=108\,\%$
von 91 bis 135	$0,40\cdot 360^\circ=144\,\%$
von 136 bis 180	$0,10\cdot 360^\circ=36\,\%$

Mit den berechneten Winkelgrößen kann das Kreisdiagramm gezeichnet werden:

Lösung 5

Volumen des äußeren Zylinders berechnen

$\begin{array}[t]{rll} V_a&=&\pi\cdot r_a^{\,\,\,2}\cdot h \\[5pt] V_a&=&\pi\cdot (d_a:2)^{2}\cdot h \\[5pt] V_a&=&\pi\cdot (8,0\,\text{cm}:2)^{2}\cdot 8,0\,\text{cm}\\[5pt] V_a&\approx&402,12\,\text{cm}^3 \end{array}$

Volumen des inneren Zylinders berechnen

$\begin{array}[t]{rll} V_i&=&\pi\cdot r_i^{\,\,\,2}\cdot h \\[5pt] V_i&=&\pi\cdot (d_i:2)^{2}\cdot h \\[5pt] V_i&=&\pi\cdot (6,0\,\text{cm}:2)^{2}\cdot 8,0\,\text{cm}\\[5pt] V_i&\approx&226,19\,\text{cm}^3 \end{array}$

Volumen des Hohlzylinders berechnen

$\begin{array}[t]{rll} V_H&=&V_a-V_i \\[5pt] V_H&=&402,12\,\text{cm}^3-226,19\,\text{cm}^3 \\[5pt] V_H&=&\underline{\underline{175,93\,\text{cm}^3 }} \end{array}$

Das Volumen des Hohlzylinders beträgt $175,93\,\text{cm}^3.$

Der Radius des Kreiskegels beträgt $r=d:2=10\,\text{cm}:2=5\,\text{cm}.$

Damit lässt sich mit dem Satz des Pythagoras die Höhe berechnen:

$\begin{array}[t]{rll} h^2+r^2&=&s^2 &\quad \scriptsize \mid\;-r^2 \\[5pt] h^2&=&s^2-r^2 &\quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt] h&=&\sqrt{s^2-r^2} \\[5pt] h&=&\sqrt{(7,8\,\text{cm})^2-(5\,\text{cm})^2} \\[5pt] h&\approx&\underline{\underline{ 6,0\,\text{cm}}} \end{array}$

Die Höhe des Kreiskegels beträgt $6,0\,\text{cm}.$