Teil B – Wahlaufgaben

Wahlaufgabe 6.1

Eine Firma errichtet einen Werbeträger auf einem zylinderförmigen Sockel (siehe Abbildung).
Dieser Werbeträger hat die Form eines dreiseitigen Prismas.
Die Seitenflächen sowie Grund- und Deckfläche des Werbeträgers bestehen aus Glas.

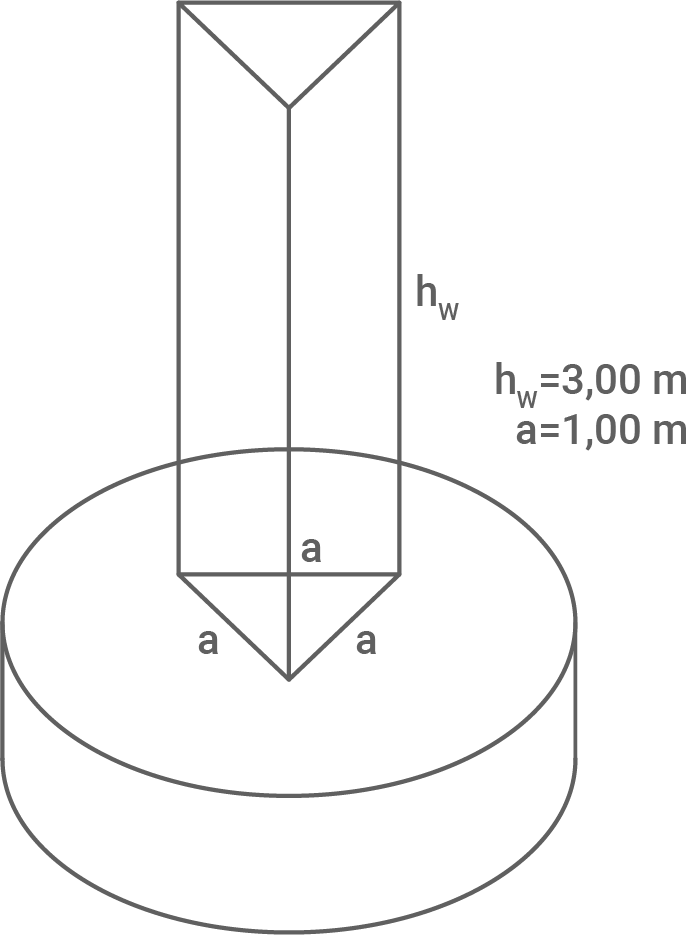
Abbildung (nicht maßstäblich)

Berechne, wie viel Quadratmeter Glas zur Herstellung des Werbeträgers benötigt werden.

Die Firma erstellt für die Herstellung, Lieferung und Montage des Werbeträgers einen Kostenvoranschlag.

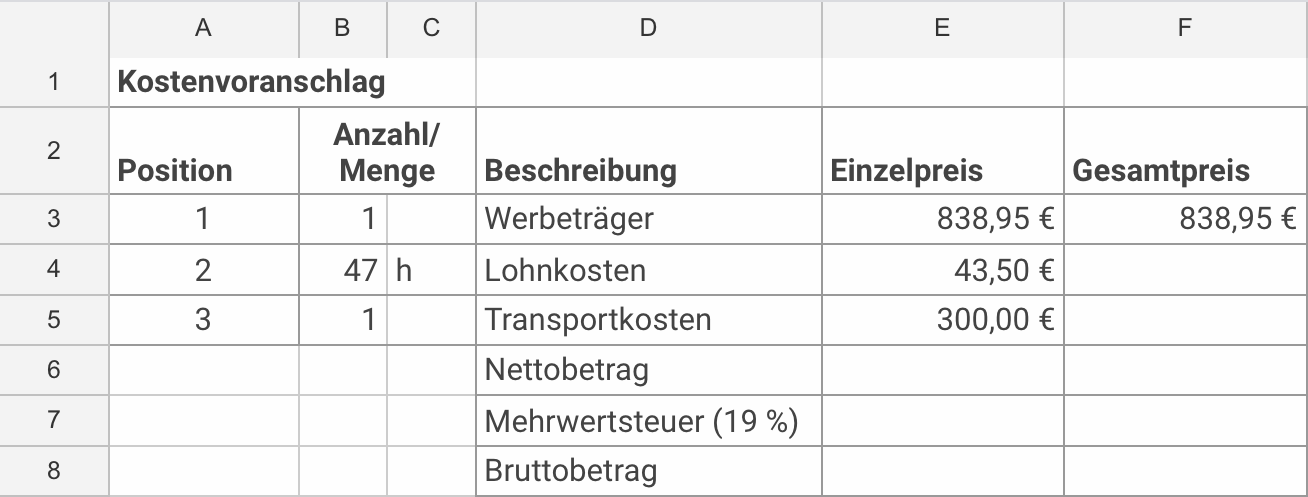Ermittle den Wert in Zelle F8.

Von dem zylinderförmigen Sockel aus Beton sind bekannt:

Radius: $1,50\,\text{m}$
Masse: $12,2\,\text{t}$
Dichte von Beton: $2,3\,\frac{\text{t}}{\text{m}^3}$

Berechne die Höhe des Sockels.

Für Wahlaufgabe 6.1 erreichbare BE: 8

Wahlaufgabe 6.2

Für ein Freizeitturnier werden zehn Mannschaften in zwei Gruppen $A$ und $B$ eingeteilt. Die Einteilung erfolgt durch Auslosen.
In einer Urne befinden sich fünf Lose $A$ und fünf Lose $B.$ Nacheinander wird für jede Mannschaft ein Los gezogen.
Das jeweils gezogene Los wird nicht zurückgelegt.

Gib die Wahrscheinlichkeit dafür an, dass zuerst ein Los $A$ gezogen wird.

Der Turnierleiter zieht zuerst ein Los für die Mannschaft „Superhelden“, anschließend für die Mannschaft „Girlfriends" und danach für alle weiteren Mannschaften.
Das Auslosen der Gruppen für die zwei Mannschaften „Superhelden“ und „Girlfriends“ ist ein zweistufiges Zufallsexperiment.

Zeichne zu diesem zweistufigen Zufallsexperiment ein Baumdiagramm und beschrifte alle Pfade mit ihren Wahrscheinlichkeiten.
Gib die Wahrscheinlichkeit dafür an, dass für beide Mannschaften ein Los $A$ gezogen wird.
Ermittle die Wahrscheinlichkeit dafür, dass für beide Mannschaften verschiedene Gruppen ausgelost werden.

In Gruppe $B$ spielt jede der fünf Mannschaften genau einmal gegen jede andere Mannschaft.
Ermittle, wie viele Spiele in der Gruppe $B$ insgesamt stattfinden müssen.

Für Wahlaufgabe 6.2 erreichbare BE: 8

Wahlaufgabe 6.3

Autofahrer sollten die Kosten für ihr Fahrzeug im Blick behalten.

Herr Lesser betankt sein Fahrzeug immer vollständig. Im Monat September notiert er dafür die folgenden Daten:

Datum	km-Stand	Kraftstoff
Datum	km-Stand	Menge	Kosten
05.09.	$62\,636$	$54,6\,\text{Liter}$	$70,98\,€$
12.09.	$63\,070$	$32,2\,\text{Liter}$	$42,18\,€$
30.09.	$63\,987$	$66,1\,\text{Liter}$	$88,56\,€$

Gib den Preis für einen Liter Kraftstoff am 05.09. an.
Berechne den durchschnittlichen Kraftstoffverbrauch pro hundert Kilometer vom 12.09. bis 30.09.

An einer Tankstelle wurde am 15.10. der Preis für einen Liter Super-E10 fünfmal geändert.
Entscheide und begründe, welches der folgenden Diagramme die Preise an diesem Tag richtig darstellt.

Diagramm A

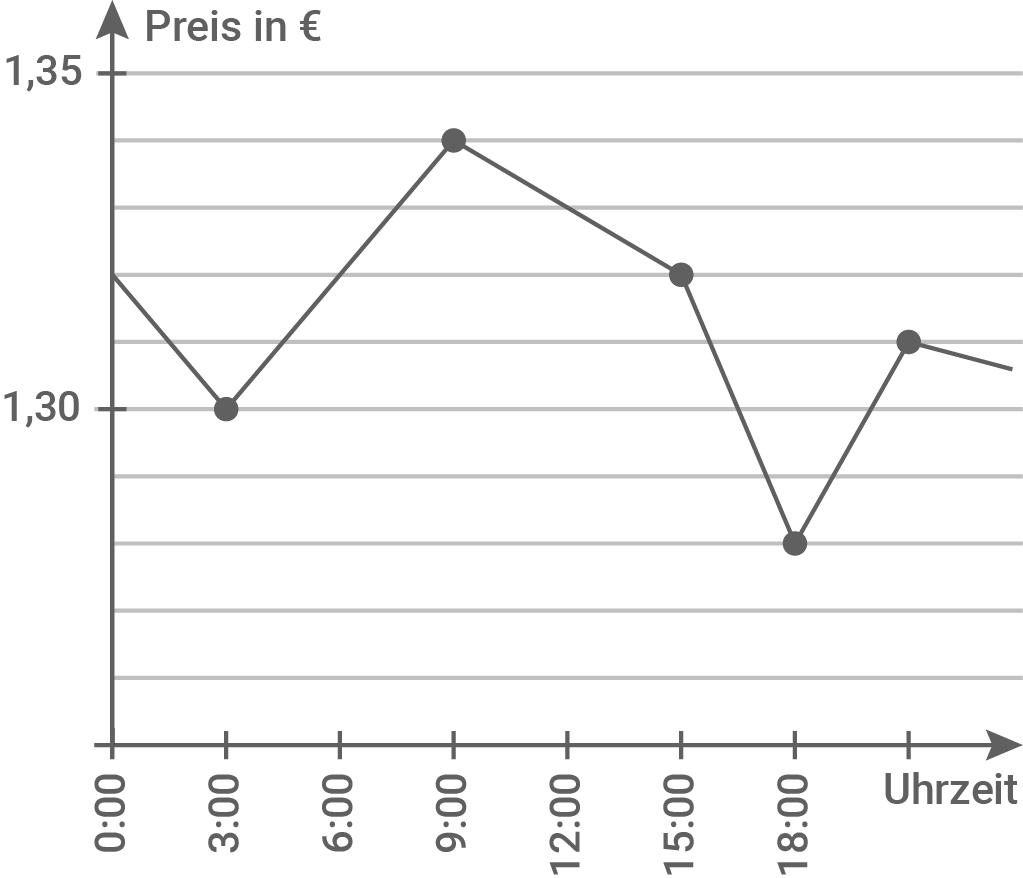
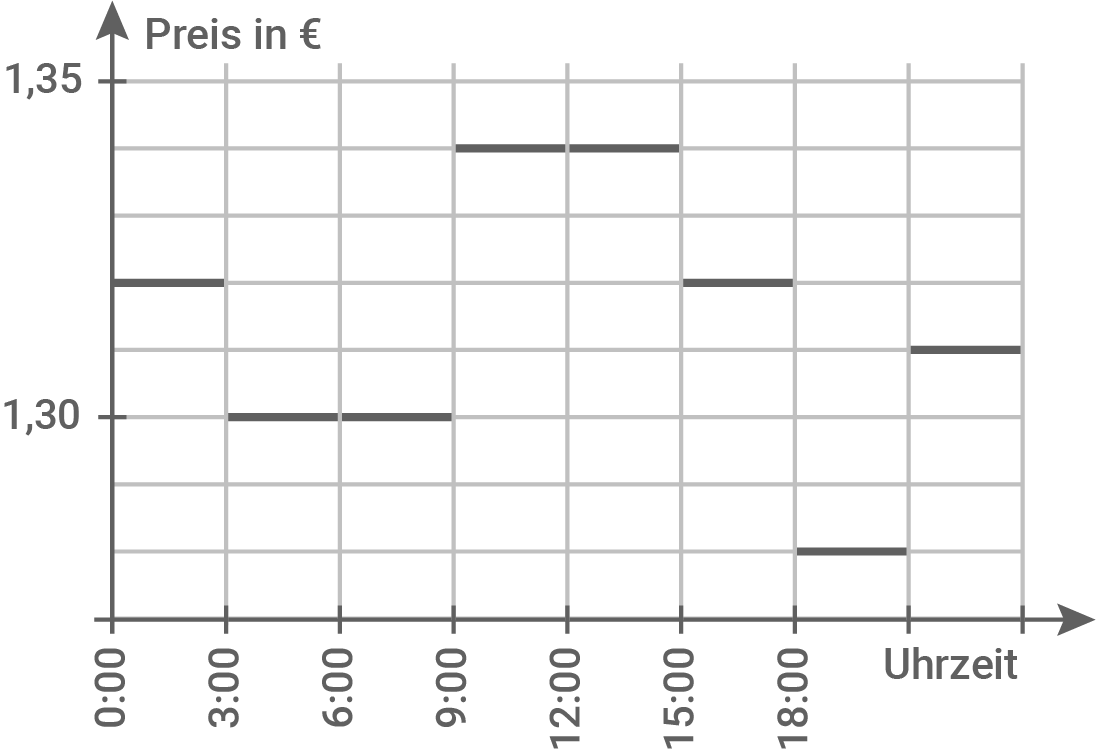
Diagramm B

Frau Wetzel verdient monatlich $2\,791,38\,€.$ Für ihr Auto hat sie die folgenden Kosten.

Kfz-Steuer: $276,00\,€$ jährlich
Auto-Versicherung: $190,86\,€$ pro Quartal
Pflege- und Werkstattkosten sowie Kraftstoff: $360,00\,€$ je Monat

Berechne, wie viel Prozent ihres Einkommens auf die Kosten für das Auto entfallen.

Für Wahlaufgabe 6.3 erreichbare BE: 8

Lösung 6.1

Grundflächeninhalt $A_G$ berechnen

Bei der Grundfläche des Werbeträgers handelt es sich um ein gleichseitiges Dreieck.

$\begin{array}[t]{rll} A_G&=&\dfrac{a^2}{4}\cdot \sqrt{3} \\[5pt] A_G&=&\dfrac{(1,00\,\text{m})^2}{4}\cdot \sqrt{3} \\[5pt] A_G&\approx&0,43\,\text{m}^2 \end{array}$

Seitenflächeninhalt $A_S$ berechnen

Bei der Seitenfläche des Werbeträgers handelt es sich um ein Rechteck.

$\begin{array}[t]{rll} A_S&=&a\cdot h_W \\[5pt] A_S&=&1,00\,\text{m}\cdot 3,00\,\text{m} \\[5pt] A_S&=&3,00\,\text{m}^2 \end{array}$

Oberflächeninhalt des Prismas berechnen

$\begin{array}[t]{lll} 2\cdot A_G+3\cdot A_S \\[5pt] = 2\cdot 0,43\,\text{m}^2+3\cdot 3,00\,\text{m}^2 \\[5pt] = \underline{\underline{ 9,86\,\text{m}^2}} \end{array}$

Zur Herstellung des Werbeträgers werden $9,86\,\text{m}^2$ Glas benötigt.

Gesamtpreis der Lohnkosten (Zelle F4) berechnen

$47\cdot 43,50\,€=2\,044,50\,€$

Gesamtpreis der Transportkosten (Zelle F5) berechnen

$1\cdot 300,00\,€=300,00\,€$

Nettobetrag (Zelle F6) berechnen

$838,95\,€+2\,044,50\,€+300,00\,€=3\,183,45\,€$

Mehrwertsteuer (Zelle F7) berechnen

$3\,183,45\,€\cdot 19\,\%=3\,183,45\,€\cdot 0,19\approx604,86\,€$

Bruttobetrag (Zelle F8) berechnen

$3\,183,45\,€+604,86\,€=\underline{\underline{ 3\,788,31\,€}}$

Der Wert in Zelle F8 beträgt $3\,788,31\,€.$

Volumen des Sockels berechnen

$\begin{array}[t]{rll} \rho&=&\dfrac{m}{V} &\quad \scriptsize \mid\;\cdot V \\[5pt] \rho\cdot V&=&m &\quad \scriptsize \mid\;:\rho\\[5pt] V&=&\dfrac{m}{\rho} \\[5pt] V&=&\dfrac{12,2\,\text{t}}{2,3\,\frac{\text{t}}{\text{m}^3}} \\[5pt] V&\approx&5,30\,\text{m}^3 \end{array}$

Höhe des Sockels berechnen

$\begin{array}[t]{rll} V&=&\pi\cdot r^2\cdot h &\quad \scriptsize \mid\;:\pi \\[5pt] \dfrac{V}{\pi}&=& r^2\cdot h &\quad \scriptsize \mid\;:r^2\\[5pt] \dfrac{V}{\pi\cdot r^2}&=&h &\\[5pt] h&=&\dfrac{V}{\pi\cdot r^2} &\\[5pt] h&=&\dfrac{5,30\,\text{m}^3}{\pi\cdot (1,50\,\text{m})^2} &\\[5pt] h&\approx&\underline{\underline{ 0,75\,\text{m}}} \end{array}$

Die Höhe des Sockels beträgt etwa $0,75\,\text{m}.$

Lösung 6.2

Es gibt insgesamt $10$ Lose. Davon sind $5$ Lose $A.$

Damit folgt:

$P(A)=\dfrac{5}{10}=\underline{\underline{ \dfrac{1}{2}}}=\underline{\underline{ 0,5}}=\underline{\underline{ 50\,\%}}$

Die Wahrscheinlichkeit beträgt $50\,\%.$

Baumdiagramm zeichnen

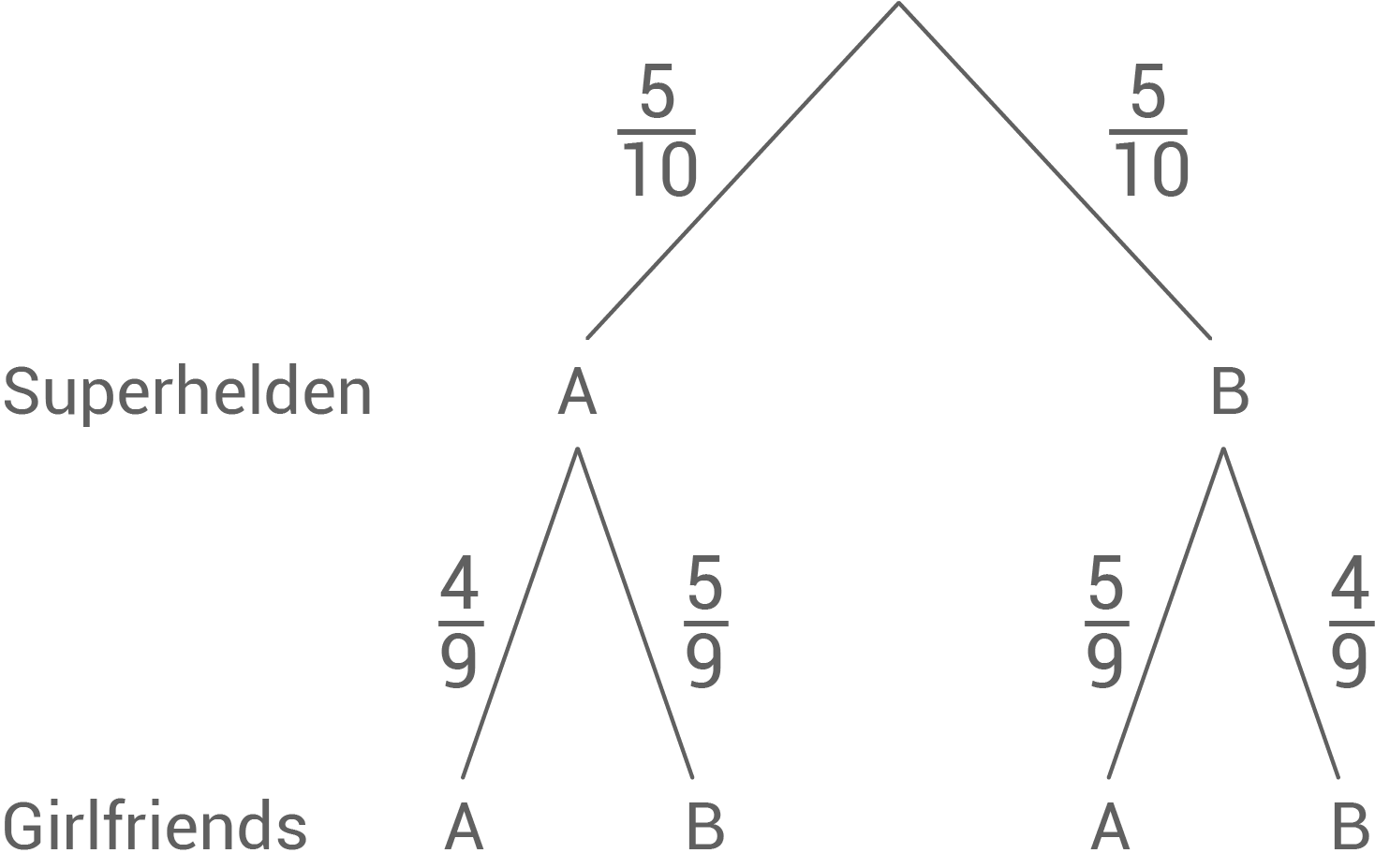Wahrscheinlichkeit angeben, dass für beide Mannschaften ein Los $\boldsymbol{A}$ gezogen wird

$P(A;A)=\dfrac{5}{10}\cdot\dfrac{4}{9}=\underline{\underline{ \dfrac{2}{9}}}\approx\underline{\underline{ 0,222}}=\underline{\underline{ 22,2\,\%}}$

Die Wahrscheinlichkeit beträgt $22,2\,\%.$

Wahrscheinlichkeit ermitteln, dass für beide Mannschaften verschiedene Gruppen ausgelost werden

$\begin{array}[t]{lll} P(A;B)+P(B;A) \\[5pt] =\dfrac{5}{10}\cdot \dfrac{5}{9}+\dfrac{5}{10}\cdot \dfrac{5}{9} \\[5pt] =\dfrac{5}{18}+\dfrac{5}{18}\\[5pt] =\underline{\underline{ \dfrac{5}{9}}} \approx \underline{\underline{ 0,556}} =\underline{\underline{ 55,6\,\%}} \end{array}$

Die Wahrscheinlichkeit beträgt $55,6\,\%.$

Es gilt:

$M_1$ spielt gegen $M_2,M_3,M_4$ und $M_5$ : $4$ Spiele
$M_2$ spielt gegen $M_3,M_4$ und $M_5$ : $3$ Spiele
$M_3$ spielt gegen $M_4$ und $M_5$ : $2$ Spiele
$M_4$ spielt gegen $M_5$ : $1$ Spiel

In Gruppe $B$ finden mit fünf Mannschaften $\underline{\underline{ 10}}$ Spielen statt.

Lösung 6.3

Preis für einen Liter Kraftstoff am 05.09. angeben

$70,98\,€:54,6=\underline{\underline{ 1,30\,€}}$

Ein Liter Kraftstoff kostete $1,30\,€.$

Durchschnittlichen Kraftstoffverbrauch pro hundert Kilometer vom 12.09. bis 30.09. berechnen

Die Fahrstrecke vom 12.09. bis 30.09. beträgt $63\,987\,\text{km}-63\,070\,\text{km}=917\,\text{km}.$

Nach $917\,\text{km}$ Fahrt musste Herr Lesser $66,1$ Liter Kraftstoff nachfüllen.

Daher gilt:

$\dfrac{66,1\ell}{917}\cdot 100\approx\underline{\underline{ 7,21\ell}}$

Der durchschnittliche Kraftstoffverbrauch pro hundert Kilometer vom 12.09. bis 30.09 betrug etwa $7,21\ell.$

Diagramm B

Begründung

Bei einer Preisänderung muss der Preis auf einen neuen Wert „springen“. Zwischen den Änderungen bleibt der Preis aber konstant. Dies trifft auf Diagramm B zu, da dort fünf Sprünge dargestellt sind und der Preis ansonsten konstant bleibt.
Bei Diagramm A würde sich der Preis an dem Tag ständig ändern.

Monatliche Kosten für ihr Auto berechnen

Kfz-Steuer: $276,00\,€:12=23,00\,€$
Auto-Versicherung: $190,86\,€:3=63,62\,€$
Pflege, Werkstatt, Kraftstoff: $360,00\,€$

Gesamtkosten für ihr Auto berechnen

$23,00\,€+63,62\,€+360,00\,€=446,62\,€$

Prozentsatz berechnen

$\dfrac{446,62\,€}{2\,791,38\,€}\approx0,16=\underline{\underline{ 16\,\%}}$

Etwa $16\,\%$ ihres Einkommens entfallen auf die Kosten für das Auto.