Teil A – Arbeitsblatt
1.
a)
b)
c)
d)
2.
Wahr oder falsch? Kreuze an.
| wahr | falsch | |
| Graphen linearer Funktionen können keine, genau eine oder zwei Nullstellen haben. | ||
| Eine Pyramide mit quadratischer Grundfläche hat fünf Kanten. |
3.
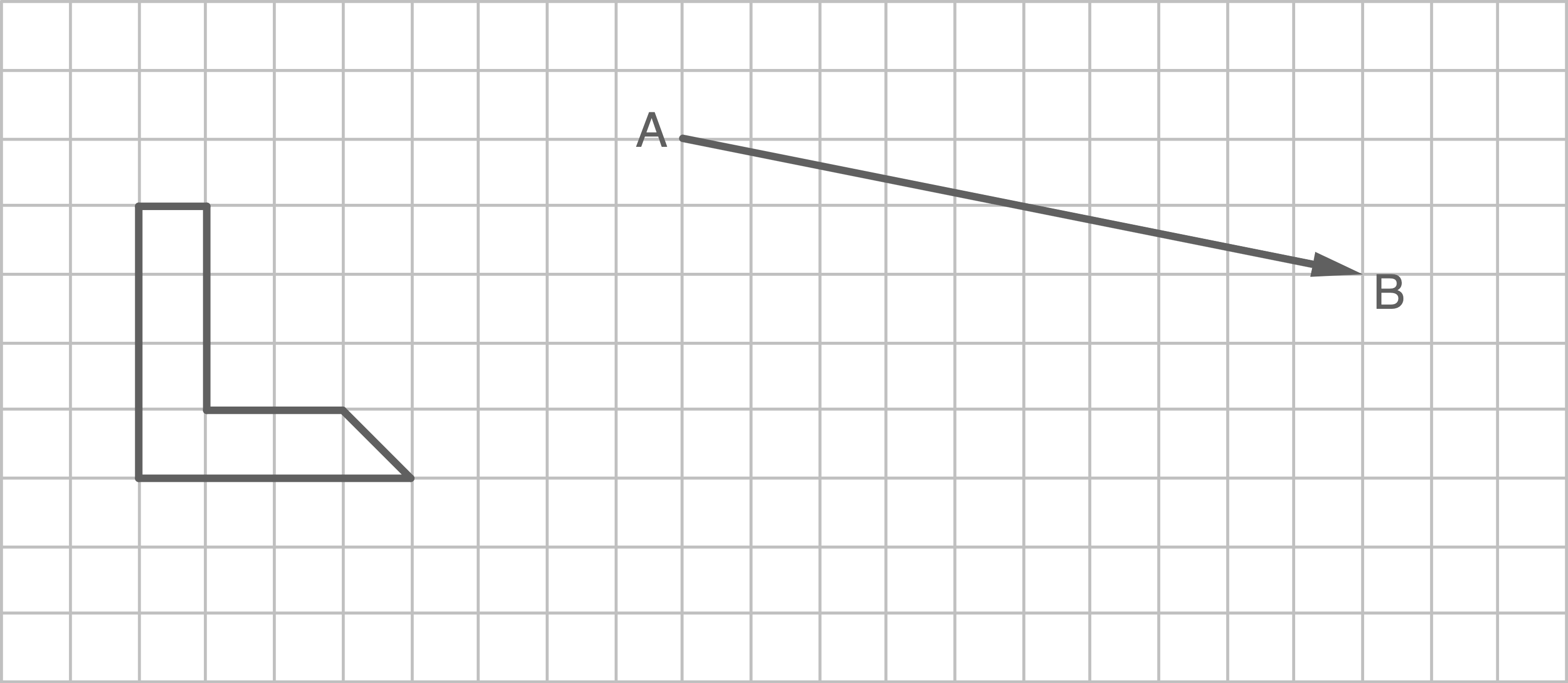
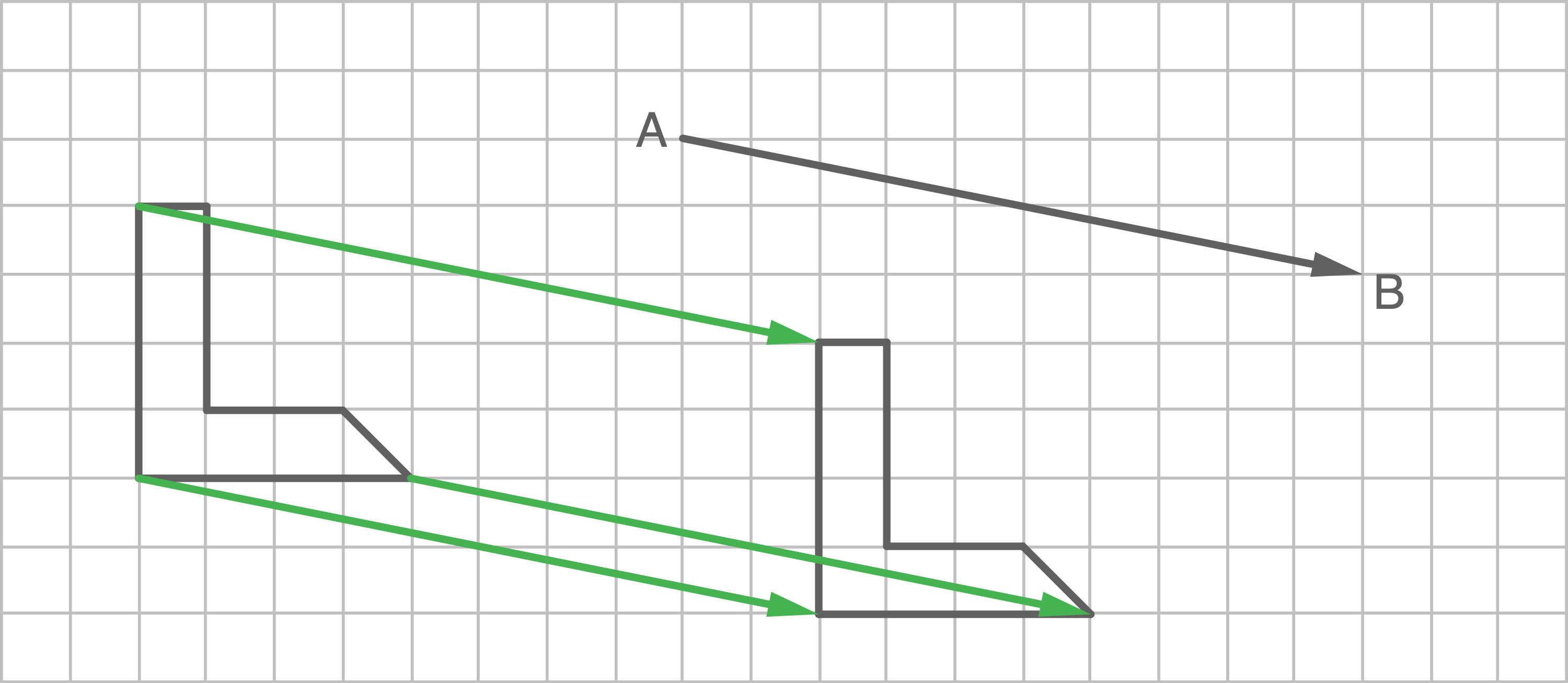
Zeichne das Bild des Sechsecks bei der Verschiebung  .
.

4.
Ordne die Volumen der Größe nach. Beginne mit dem kleinsten Volumen.



5.
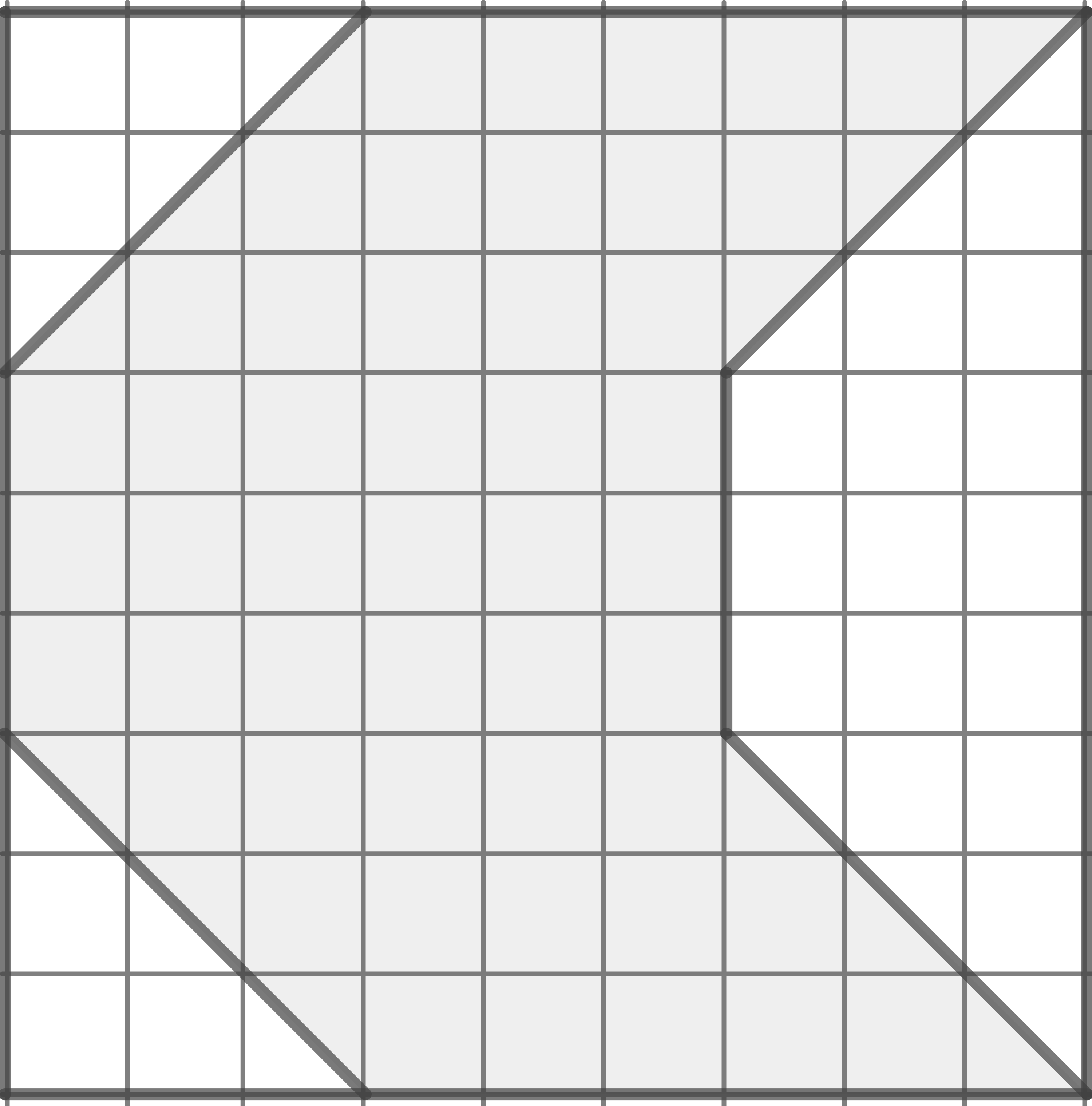
Gib den Anteil der grauen Fläche an der Gesamtfläche der Figur an.
6.
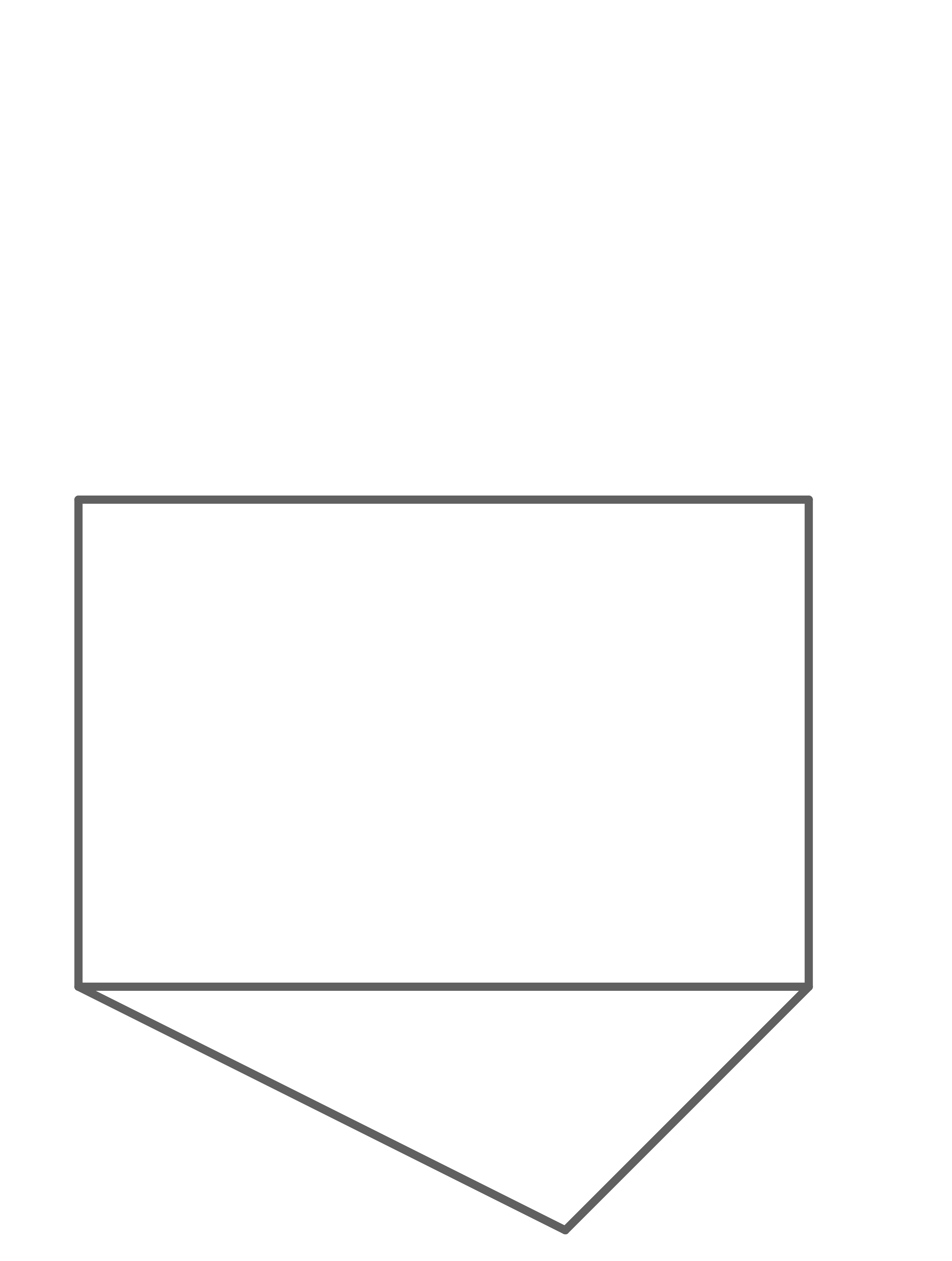
Vervollständige die Zeichnung zum Netz eines Prismas.

7.
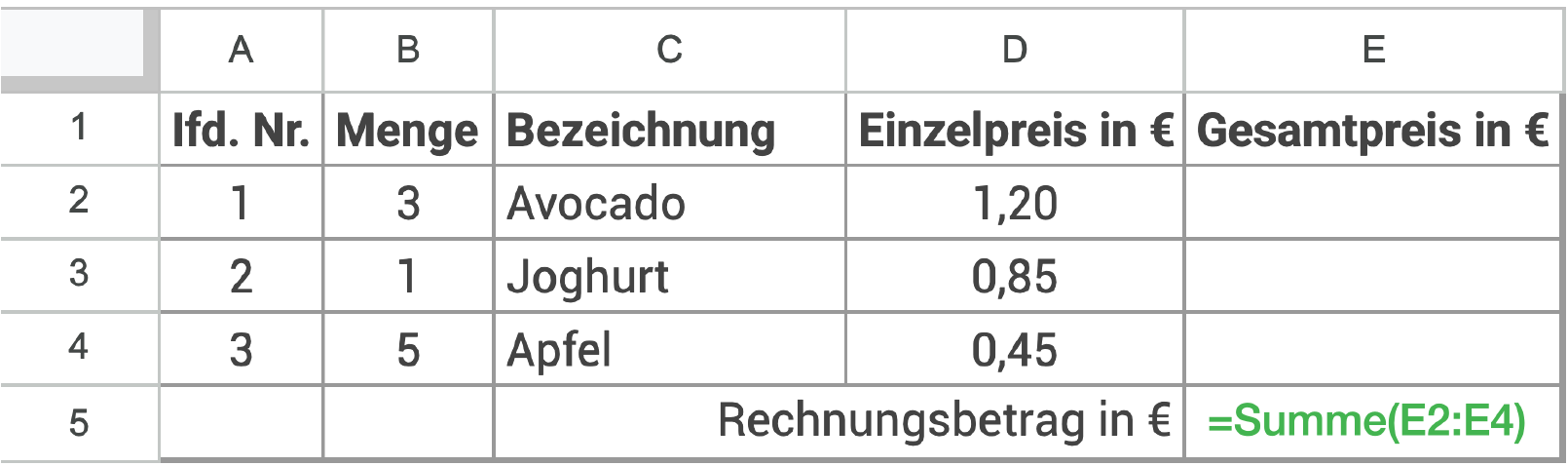
In der nachfolgenden Tabelle sollen Berechnungen automatisch angepasst werden.
Trage die Formel =Summe(E2:E4) in die entsprechende Zelle ein.
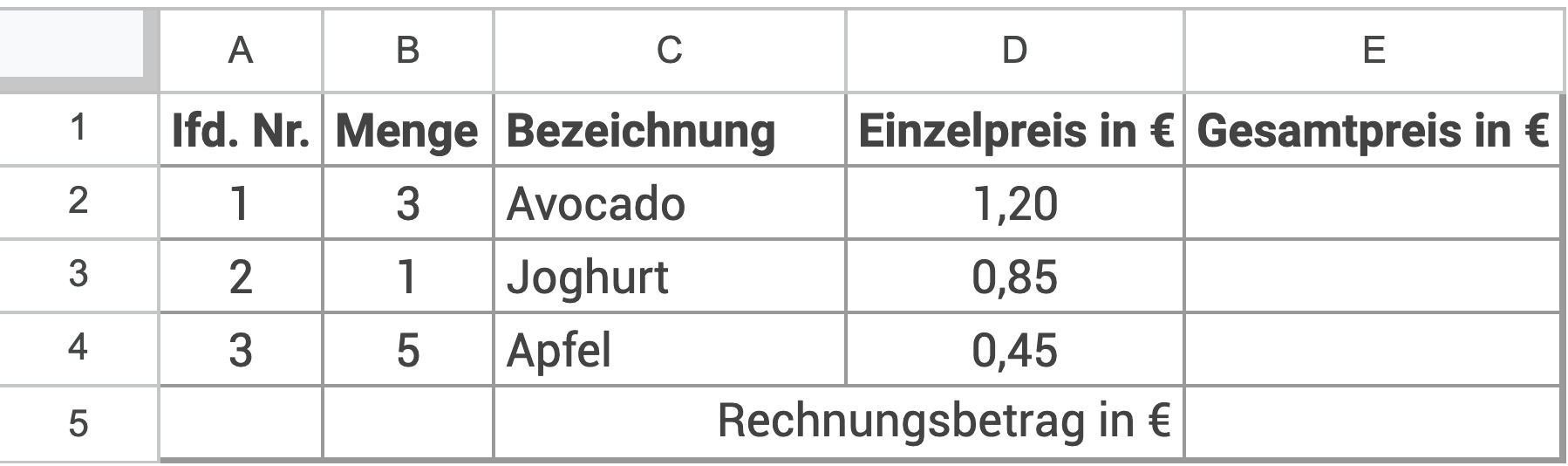
Trage die Formel =Summe(E2:E4) in die entsprechende Zelle ein.

8.
In einem Dreieck  sind die Seiten
sind die Seiten 
 und
und  lang.
lang.
Welche Dreiecksart liegt vor? Kreuze an.
Welche Dreiecksart liegt vor? Kreuze an.
| Ungleichseitiges spitzwinkliges Dreieck | |
| Ungleichseitiges rechtwinkliges Dreieck | |
| Gleichschenkliges rechtwinkliges Dreieck | |
| Gleichschenkliges stumpfwinkliges Dreieck |
9.
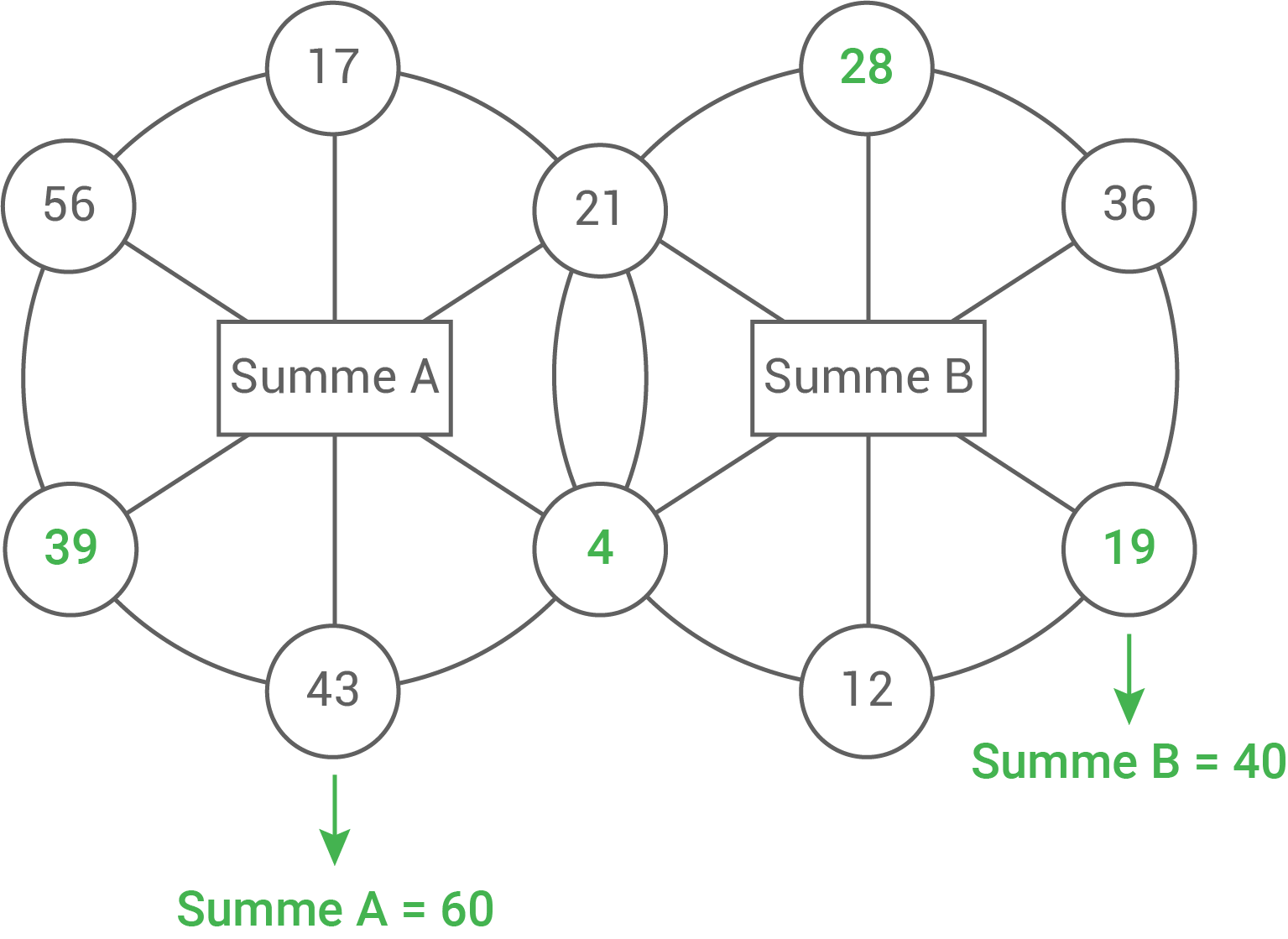
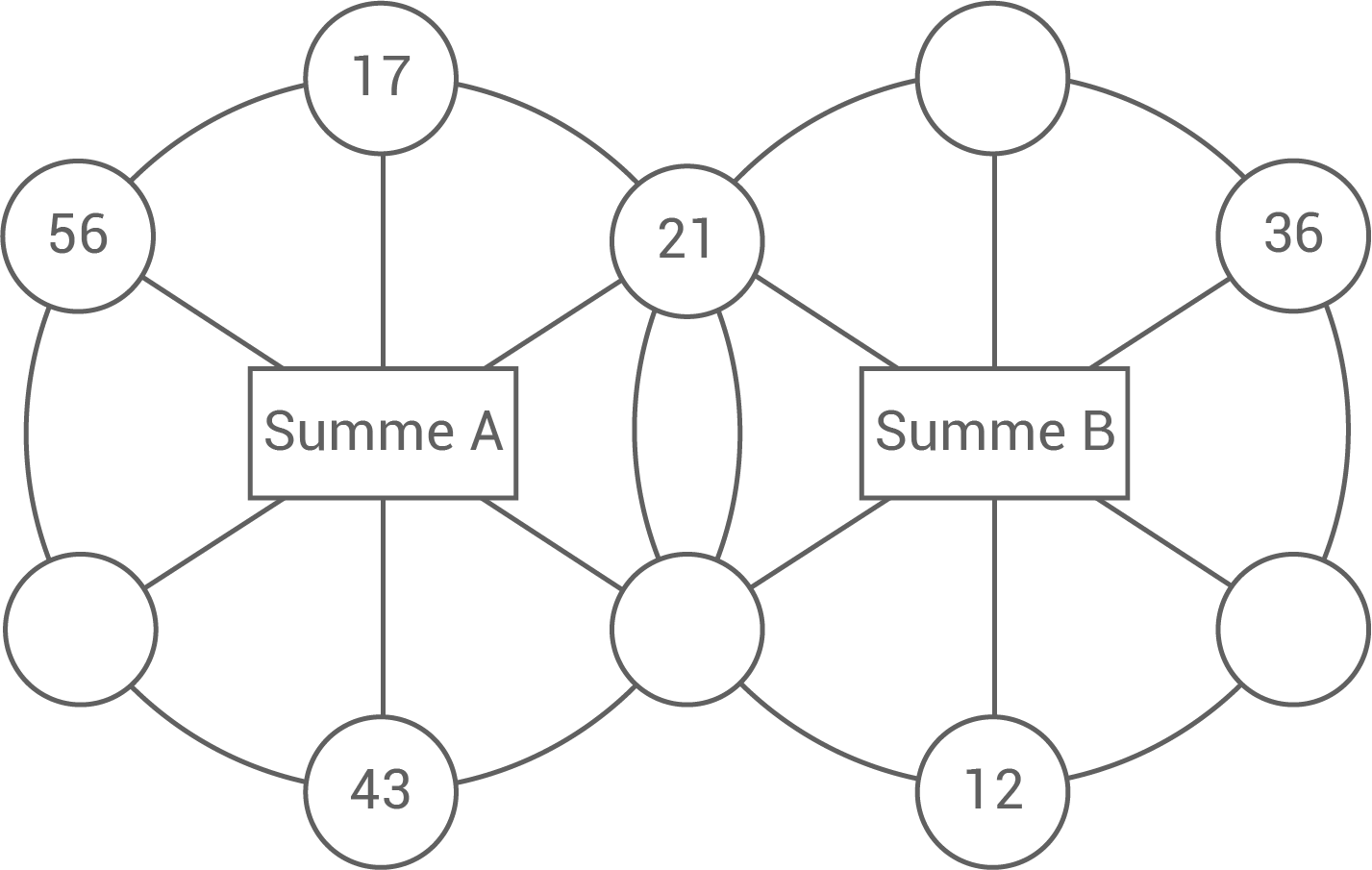
In jedem der beiden Kreise haben gegenüberliegende Zahlen die gleiche Summe. Die Summe A und die Summe B sind ungleich.
Trage alle fehlenden Zahlen ein.
Für Teil A erreichbare BE: 12
1.
a)
b)
c)
d)
2.
| wahr | falsch | |
| Graphen linearer Funktionen können keine, genau eine oder zwei Nullstellen haben. | ||
| Eine Pyramide mit quadratischer Grundfläche hat fünf Kanten. |
- Der Graph einer linearen Funktion ist eine Gerade, die entweder steigend, fallend oder parallel zur
-Achse verläuft. Graphen linearer Funktionen können somit genau eine oder keine Nullstelle haben.
- Eine Pyramide mit quadratischer Grundfläche hat acht Kanten.
3.
4.
Um die Volumen vergleichen zu können, werden diese auf eine Einheit umgerechnet, z.B.  :
:

5.
Es gibt insgesamt  Kästchen.
Davon bilden
Kästchen.
Davon bilden  Kästchen die graue Fläche.
Der Anteil der grauen Fläche an der Gesamtfläche beträgt
Kästchen die graue Fläche.
Der Anteil der grauen Fläche an der Gesamtfläche beträgt 
6.
Mit dem Zirken werden die Seitenlängen übertragen:
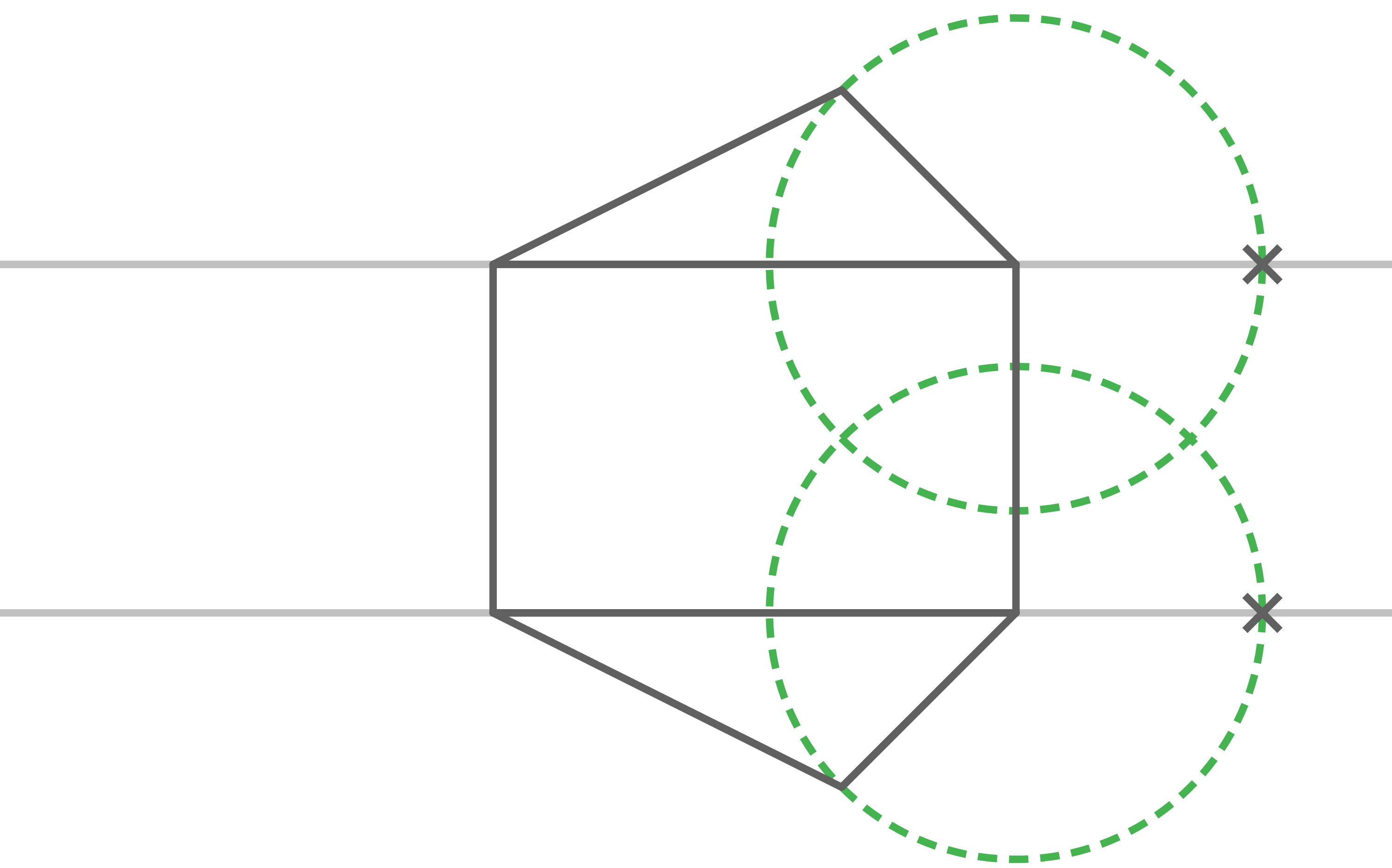
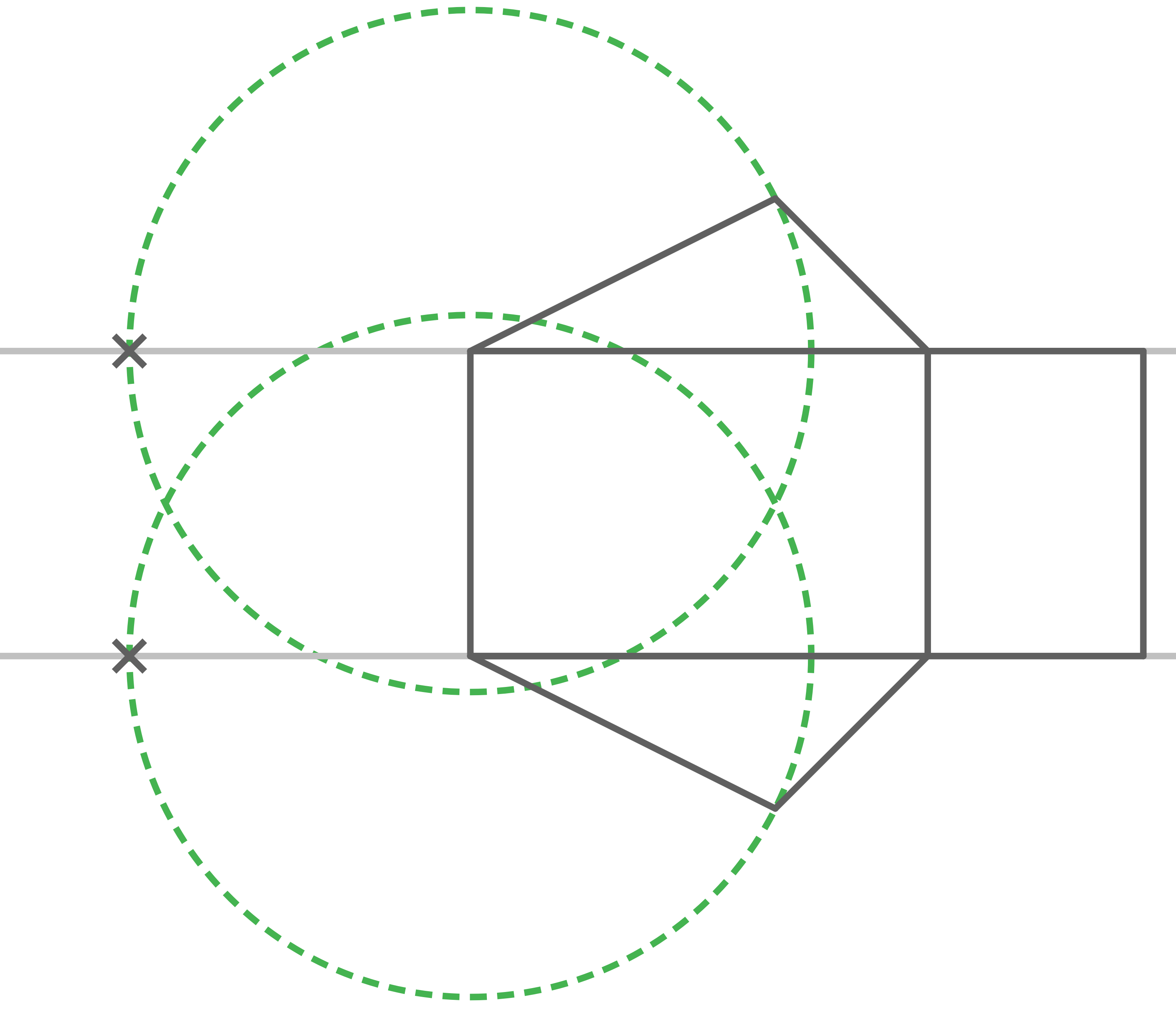 Damit ergibt sich das fertige Netz:
Damit ergibt sich das fertige Netz:
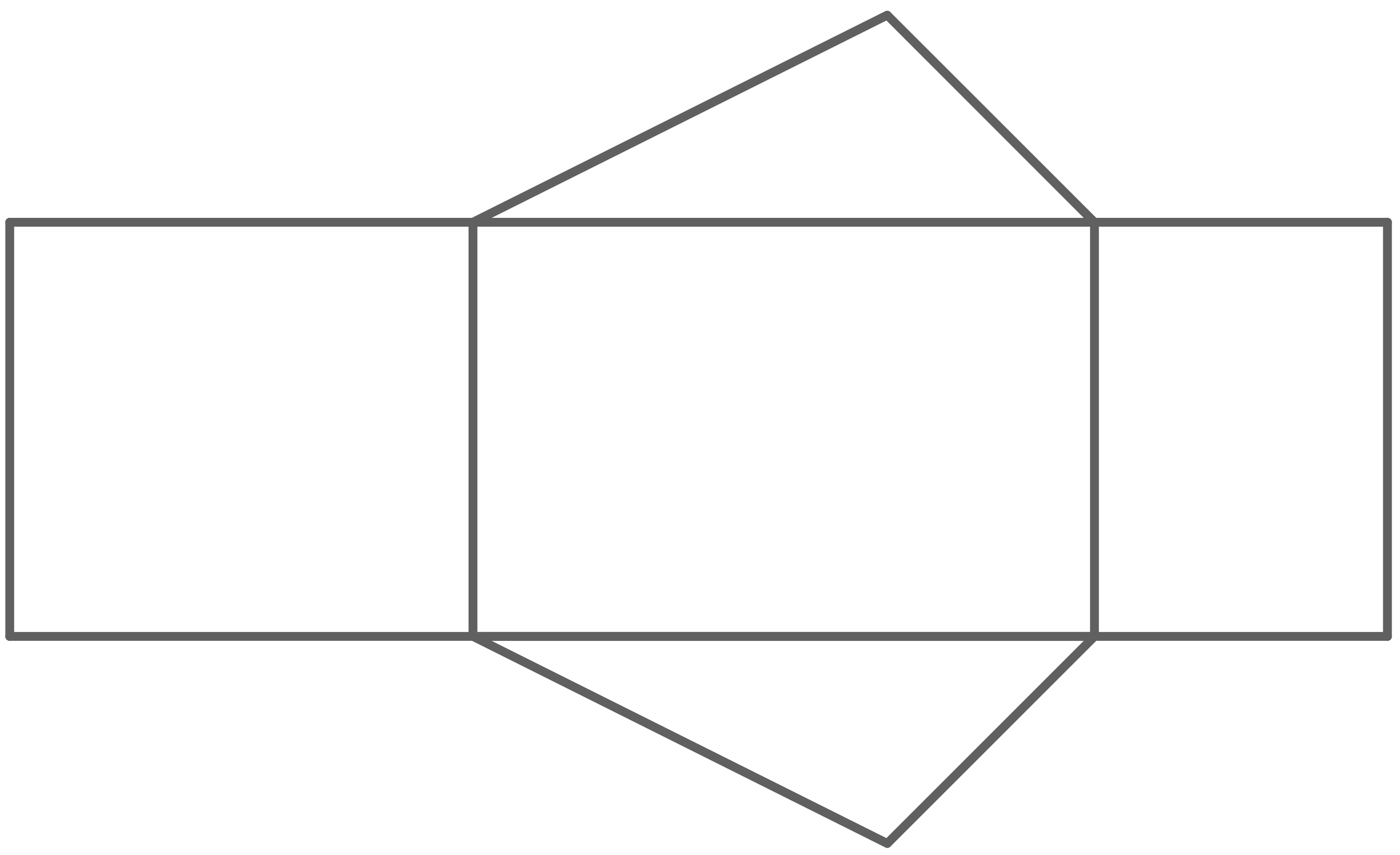



7.
8.
| Ungleichseitiges spitzwinkliges Dreieck | |
| Ungleichseitiges rechtwinkliges Dreieck | |
| Gleichschenkliges rechtwinkliges Dreieck | |
| Gleichschenkliges stumpfwinkliges Dreieck |
Um zu überprüfen, ob es sich um ein „Ungleichseitiges rechtwinkliges Dreieck“ handelt, wird der Satz des Pythagoras angewendet:
9.