A – Wahlaufgaben

Analysis (Niveau 1)

Gegeben ist die in $\mathbb R$ definierte Funktion $f$ mit $f(x)=\frac{1}{8}x^3-\frac{3}{8}x^2-1.$
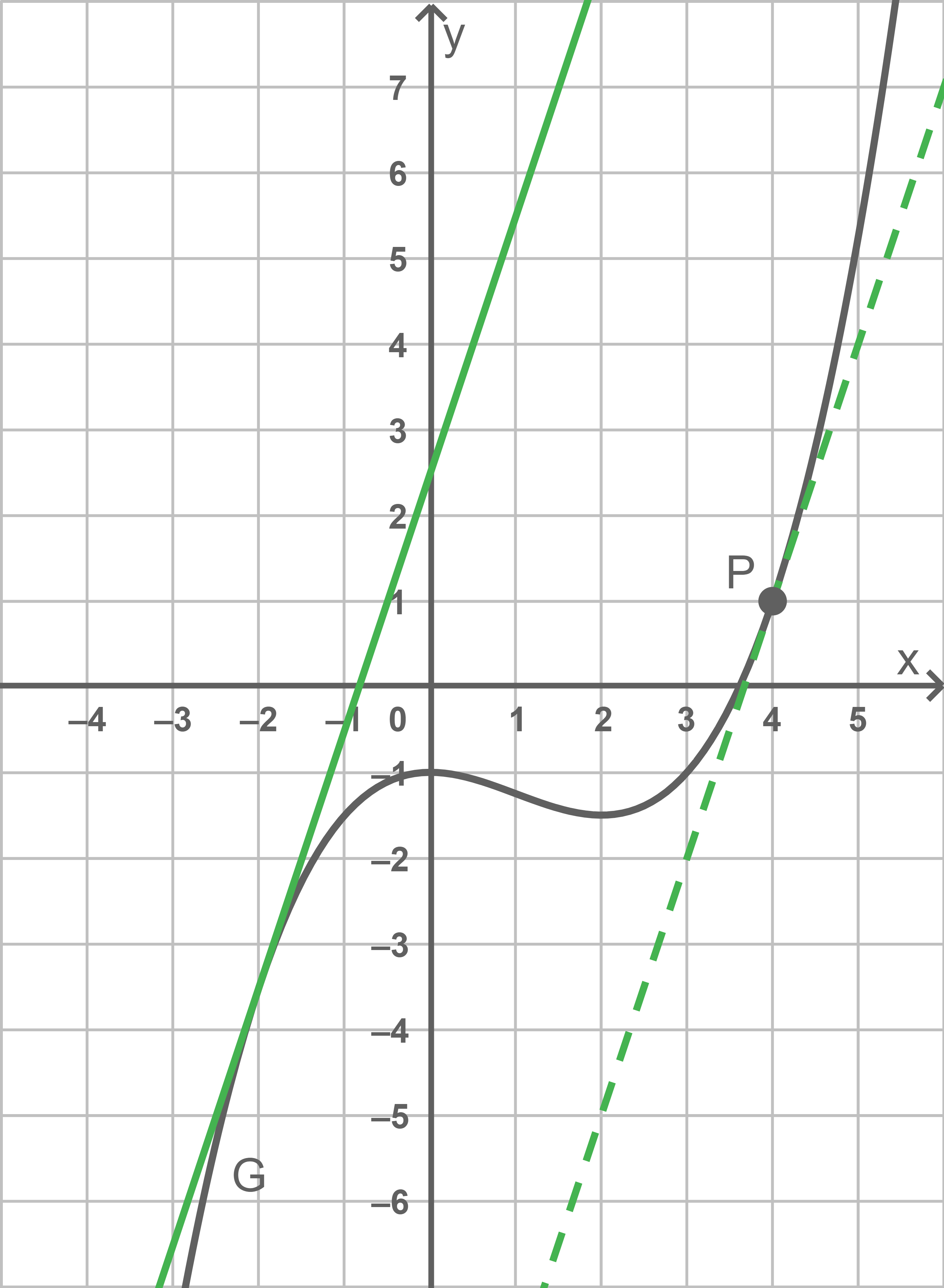
Die Abbildung zeigt den Graphen $G$ von $f.$ Die Tangente an $G$ im Punkt $P(4\mid 1)$ wird mit $t$ bezeichnet.

4.1

Bestimme rechnerisch eine Gleichung von $t.$

(3 BE)

4.2

Es gibt genau eine weitere Tangente an $G,$ die parallel zu $t$ verläuft.
Skizziere diese in der Abbildung.

(2 BE)

Lineare Algebra / Analytische Geometrie (Niveau 1)

Gegeben ist die Gerade $g:\overrightarrow{x}= \pmatrix{8\\3\\-3}+s\cdot \pmatrix{-4\\0\\3}$ mit $s \in \mathbb{R}.$

5.1

Zeige, dass der Punkt $P(4\mid 3\mid 3)$ nicht auf $g$ liegt.
Gib die Koordinaten eines Punktes $Q$ an, der auf $g$ liegt und sich nur in einer Koordinate von $P$ unterscheidet.

(3 BE)

5.2

Die Gerade $h$ verläuft parallel zur $y$ -Achse und schneidet $g$ im Punkt $(8\mid 3\mid -3).$
Untersuche, ob $g$ und $h$ senkrecht zueinander verlaufen.

(2 BE)

Stochastik (Niveau 1)

In einer Schwimmgruppe, zu der 20 Kinder gehören, haben 9 Kinder das Schwimmabzeichen Bronze.

6.1

Zwei Kinder der Schwimmgruppe werden zufällig ausgewählt. Berechne die Wahrscheinlichkeit dafür, dass diese beiden Kinder das Schwimmabzeichen Bronze haben.

(2 BE)

6.2

Gib die Bedeutung des folgenden Terms im Sachzusammenhang an:
$\frac{\pmatrix{9\\2}\cdot \pmatrix{11\\4}}{\pmatrix{20\\6}}$

(3 BE)

Analysis (Niveau 2)

Gegeben ist die in $\mathbb R$ definierte Funktion $f$ durch $f(x)=(2x-8)\cdot \mathrm e^{5-x}.$

7.1

Berechne die Koordinaten des einzigen Extrempunktes $E(x_E\mid f(x_E))$ des Graphen von $f.$
Die Untersuchung der notwendigen Bedingungen ist dabei ausreichend.

(4 BE)

7.2

Es gilt: $\(f$ und $\(f$
Erläutere, was dies für den Extrempunkt aus Aufgabe 7.1 bedeutet.

(1 BE)

Lineare Algebra / Analytische Geometrie (Niveau 2)

Die Ebene $E$ wird durch die Gleichung $\overrightarrow{x}=\pmatrix{1\\-3\\0}+r\cdot \pmatrix{-3\\4\\1}+s\cdot \pmatrix{3\\-4\\0}$ mit $r,s \in\mathbb R$ beschrieben.

8.1

Zeige, dass der Vektor $\pmatrix{4\\3\\0}$ senkrecht zur Ebene $E$ steht.

(2 BE)

8.2

Bestimme die Koordinaten eines Punktes $P$ mit folgender Eigenschaft:
Wird der Punkt $P$ an der Ebene $E$ gespiegelt, so hat der entstehende Punkt vom Punkt $P$ den Abstand $20.$

(3 BE)

Stochastik (Niveau 2)

Eine faire Münze wird zehnmal geworfen. Die Zufallsgröße $X$ beschreibt die Anzahl der gefallenen Wappen bei den zehn Würfen. Eine der drei abgebildeten Wahrscheinlichkeitsverteilungen stellt die Verteilung der Zufallsgröße $X$ dar.

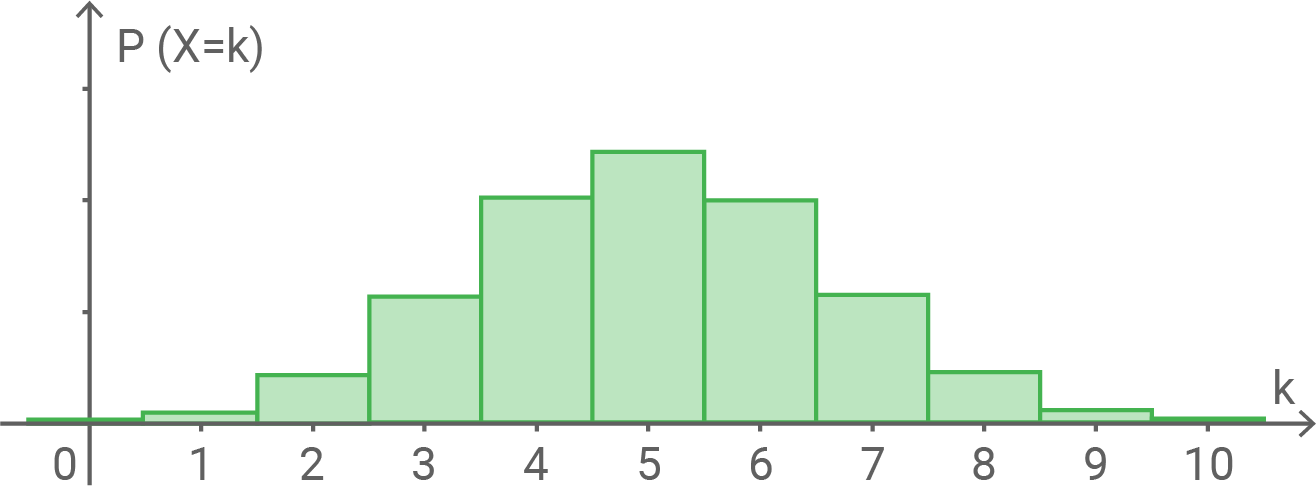
Wahrscheinlichkeitsverteilung 1

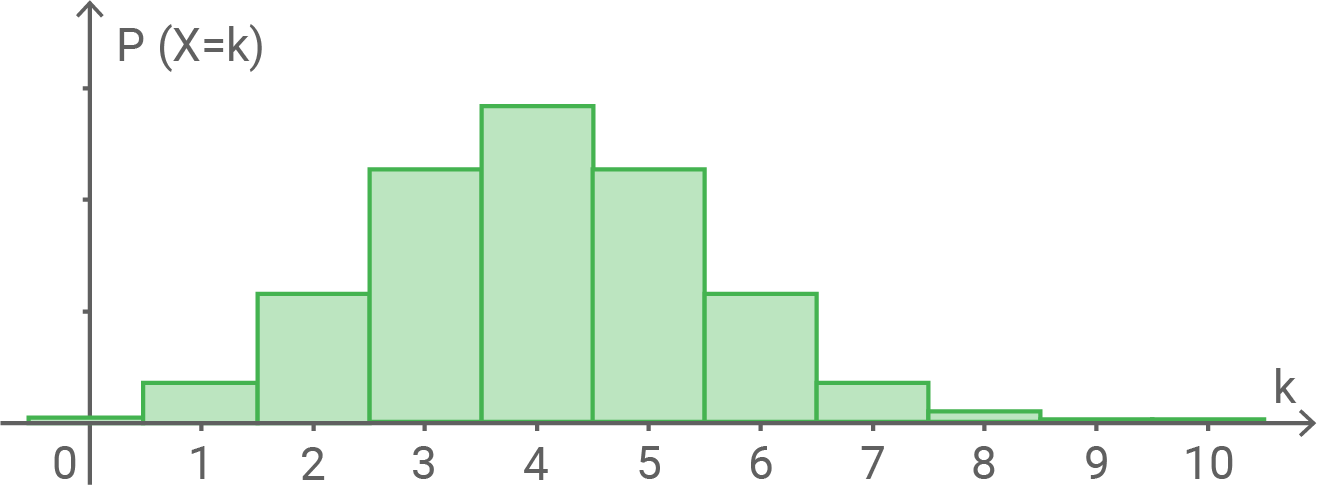
Wahrscheinlichkeitsverteilung 2

Wahrscheinlichkeitsverteilung 3

9.1

Entscheide begründet, welche beiden Wahrscheinlichkeitsverteilungen nicht die Verteilung der Zufallsgröße $X$ darstellen.

(2 BE)

9.2

Es gilt: $P(X\leq 3)\approx 0,17.$
Berechne $P(4\leq X \leq 6)$ und erläutere deinen Ansatz.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Analysis (Niveau 1)

4.1

$\(f$

Die allgemeine Gleichung der Tangente lautet $y=m\cdot x+b.$

Für $m$ folgt:

$\(\begin{array}[t]{rlll} m&=&f$

Einsetzen von $P(4\mid 1)$ in die Gleichung liefert dann:

$\begin{array}[t]{rlll} 1&=&3\cdot4+b &\mid\;-12 \\[5pt] -11&=&b \end{array}$

Die Gleichung der Tangente $t$ lautet somit:

$t:y=3x-11$

4.2

Lineare Algebra/Analytische Geometrie (Niveau 1)

5.1

Aus dem Ansatz $\pmatrix{4\\3\\3}=\pmatrix{8\\3\\-3}+s\cdot \pmatrix{-4\\0\\3}$ folgt in der ersten Koordinate $s=1$ und in der dritten Koordinate $s=2.$ Somit liegt der Punkt $P$ nicht auf $g.$

Einsetzen von $s=1$ liefert in der dritten Koordinate der Geradengleichung $0.$ Somit sind $Q(4\mid 3\mid 0)$ mögliche Koordinaten.

5.2

Da $h$ parallel zur $y$ -Achse verläuft, ist $\pmatrix{0\\1\\0}$ ein Richtungsvektor von $h.$ Wegen $\pmatrix{-4\\0\\3}\circ \pmatrix{0\\1\\0}=0$ verlaufen $g$ und $h$ senkrecht zueinander.

Stochastik (Niveau 1)

6.1

$\dfrac{9}{20}\cdot \dfrac{8}{19}=\dfrac{72}{380}$

6.2

Der Term gibt die Wahrscheinlichkeit dafür an, dass in einer zufälligen Auswahl von sechs Kindern der Schwimmgruppe zwei Kinder das Schwimmabzeichen Bronze haben.

Analysis (Niveau 2)

7.1

$\(f$ $=(10-2x)\cdot \mathrm e^{5-x}$

Die notwendige Bedingung für Extrempunkte ist $\(f$

Damit folgt:

$\(\begin{array}[t]{rlll} f$

Da die $\mathrm e$ -Funktion stets größer als Null ist, folgt mit dem Satz des Nullprodukts:

$\begin{array}[t]{rlll} 10-2x_E&=&0 &\mid\;-10 \\[5pt] -2x_E&=&-10 &\mid\;:(-2) \\[5pt] x_E&=&5 \end{array}$

Einsetzen in $f$ liefert:

f(5)=(2\cdot5-8)\cdot\mathrm e^{5-5}=2

Somit ergeben sich die Koordinaten $E(5\mid2).$

7.1

Da die Steigung links von der Extremstelle positiv und rechts davon negativ ist, ist der Extrempunkt $E$ ein Hochpunkt.

Lineare Algebra/Analytische Geometrie (Niveau 2)

8.1

$\begin{array}[t]{rlll} \pmatrix{4\\3\\0}\circ\pmatrix{-3\\4\\1}&=&-12+12 \\[5pt] &=&0 \end{array}$

$\begin{array}[t]{rlll} \pmatrix{4\\3\\0}\circ\pmatrix{3\\-4\\0}&=&12-12 \\[5pt] &=&0 \end{array}$

Da der Vektor senkrecht zu beiden Spannvektoren der Ebene liegt, steht er somit auch senkrecht zur Ebene $E.$

8.2

Für die Länge des Vektors aus Teilaufgabe 8.1 gilt:

$\begin{array}[t]{rlll} \left\vert\pmatrix{4\\3\\0}\right\vert&=&\sqrt{4^2+3^2+0^2} \\[5pt] &=&\sqrt{25} \\[5pt] &=&5 \end{array}$

Ein Punkt auf der Ebene, z.B. der Stützpunkt, der zweimal um diesen Vektor bewegt wird, liegt somit $10\;\text{LE}$ von der Ebene entfernt und der Abstand zu dem gespiegelten Punkt beträgt damit $20\;\text{LE}.$ Es folgt:

$\begin{array}[t]{rlll} \overrightarrow{OP}&=&\pmatrix{1\\-3\\0}+2\cdot\pmatrix{4\\3\\0} \\[5pt] &=&\pmatrix{9\\3\\0} \end{array}$

Mögliche Koordinaten für $P$ sind somit durch $P(9\mid3\mid0)$ gegeben.

Stochastik (Niveau 2)

9.1

Die Wahrscheinlichkeit Wappen bzw. Zahl zu erzielen ist gleichgroß und zwar jeweils $0,5.$ Damit muss die Wahrscheinlichkeitsverteilung symmetrisch um den Erwartungswert liegen, welcher bei der Hälfte der Würfe, d.h. hier bei $5$ liegt. Dort liegt zudem die größte Wahrscheinlichkeit vor.

Die Wahrschinelichkeitsverteilung 1 ist nicht symmetrische um $k=5,$ währende die Wahrscheinlichkeitsverteilung 3 bei $k=4$ die größte Wahrscheinlichkeit vorliegen hat.
Somit können beide diese Wahrscheinlichkeitsverteilungen nicht die Zufallsgröße $X$ darstellen.

9.2

Wie in Teilaufgabe 9.1 bereits gesehen, ist die Wahrscheinlichkeitsverteilung von $X$ symmetrisch um den Erwartungswert $5.$ Somit gilt $P(X\leq3)=P(X\geq7).$ Damit folgt für die gesuchte Wahrscheinlichkeit:

Rechenweg anzeigen

$P(4\leq X\leq 6) \approx 0,66$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?