C - Stochastik
1
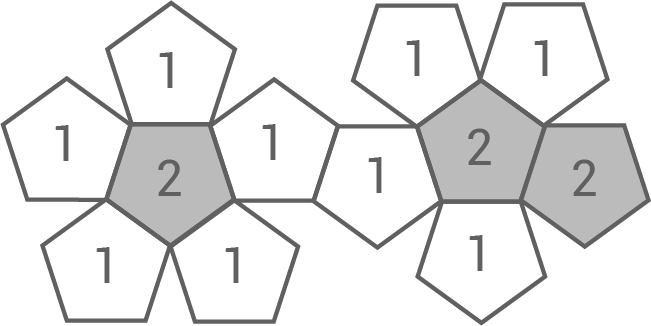
Bei einem  -seitigen Spielwürfel fallen alle Seiten bei einem Wurf jeweils mit der gleichen Wahrscheinlichkeit. Jede Seite des Spielwürfels ist gemäß dem abgebildeten Netz mit einer der Zahlen 1 und 2 beschriftet.
-seitigen Spielwürfel fallen alle Seiten bei einem Wurf jeweils mit der gleichen Wahrscheinlichkeit. Jede Seite des Spielwürfels ist gemäß dem abgebildeten Netz mit einer der Zahlen 1 und 2 beschriftet.
1.1
Bestimme unter Angabe einer geeigneten Zufallsgröße die Wahrscheinlichkeiten der folgenden Ereignisse:


Bei  Würfen fällt genau
Würfen fällt genau  -mal die Zahl
-mal die Zahl 
Bei  Würfen fällt mindestens
Würfen fällt mindestens  -mal aber höchstens
-mal aber höchstens  -mal die Zahl
-mal die Zahl 
(5 BE)
1.2
Für ein Gewinnspiel wird der Spielwürfel bei jedem Spiel viermal geworfen. Man betrachtet die Augensumme der vier Würfe.
1.2.1
Begründe, dass die Wahrscheinlichkeit dafür, dass die Summe der geworfenen Zahlen  ist, größer ist als die Wahrscheinlichkeit dafür, dass die Summe der geworfenen Zahlen
ist, größer ist als die Wahrscheinlichkeit dafür, dass die Summe der geworfenen Zahlen  ist.
ist.
(2 BE)
1.2.2
Einen Hauptpreis erhält eine Spielerin bzw. ein Spieler, wenn die Summe der geworfenen Zahlen mindestens  ist. Zeige, dass auf lange Sicht im Mittel etwa bei einem von zwanzig Spielen ein Hauptpreis vergeben wird.
ist. Zeige, dass auf lange Sicht im Mittel etwa bei einem von zwanzig Spielen ein Hauptpreis vergeben wird.
(3 BE)
1.2.3
Die Wahrscheinlichkeit dafür, dass bei einem Spiel ein Trostpreis vergeben wird, beträgt 
Gib den Spielausgang an, bei dem die Spielerin bzw. der Spieler einen Trostpreis erhält, und begründe deine Angabe.
Gib den Spielausgang an, bei dem die Spielerin bzw. der Spieler einen Trostpreis erhält, und begründe deine Angabe.
(2 BE)
1.2.4
Beurteile jede der beiden folgenden Aussagen:


Wird bei einmaligem Werfen des Spielwürfels die geworfene Zahl betrachtet, so handelt es sich um ein Bernoulli-Experiment.
Wird bei mehrfacher Durchführung des beschriebenen Spiels jeweils festgehalten, ob ein Trostpreis oder ob ein Hauptpreis vergeben wird, so handelt es sich um eine Bernoulli- Kette.
(4 BE)
2
Ein Supermarkt bietet Nass- und Trockenfutter für Hunde jeweils in einer normalen Variante und in einer energiereduzierten Light-Variante an. Im Folgenden werden ausschließlich Kundinnen und Kunden betrachtet, die sich bei einem Kauf von Hundefutter für genau eine dieser vier Varianten entscheiden. Zwei Drittel dieser Personen kaufen Trockenfutter,  davon entscheiden sich für die Light-Variante. Von den Personen, die Nassfutter kaufen, entscheiden sich nur
davon entscheiden sich für die Light-Variante. Von den Personen, die Nassfutter kaufen, entscheiden sich nur  für die Light-Variante.
Von den betrachteten Kundinnen und Kunden wird eine Person zufällig ausgewählt. Untersucht werden die folgenden Ereignisse:
für die Light-Variante.
Von den betrachteten Kundinnen und Kunden wird eine Person zufällig ausgewählt. Untersucht werden die folgenden Ereignisse:


„Die Person kauft Trockenfutter.“
„Die Person entscheidet sich für eine der beiden Light-Varianten.“
2.1
Stelle den Sachzusammenhang in einem beschrifteten Baumdiagramm dar.
(4 BE)
2.2
Zeige, dass die Wahrscheinlichkeit dafür, dass das Ereignis  eintritt,
eintritt,  beträgt.
beträgt.
(2 BE)
2.3
Die zufällig ausgewählte Person entscheidet sich für eine der beiden Light-Varianten.
Berechne die Wahrscheinlichkeit dafür, dass es sich um Nassfutter handelt.
Berechne die Wahrscheinlichkeit dafür, dass es sich um Nassfutter handelt.
(4 BE)
2.4
Der Leiter des Supermarktes vermutet, dass der Anteil der Personen, die Trockenfutter kaufen, gestiegen ist, und möchte die Bestellmengen von Trockenfutter erhöhen. Vorher soll die Vermutung des Leiters mit Hilfe eines geeigneten Hypothesentests überprüft werden. Dazu werden  zufällig ausgewählte Käuferinnen und Käufer von Hundefutter betrachtet, die sich entweder für Trockenfutter oder für Nassfutter entscheiden.
Getestet wird die Nullhypothese
zufällig ausgewählte Käuferinnen und Käufer von Hundefutter betrachtet, die sich entweder für Trockenfutter oder für Nassfutter entscheiden.
Getestet wird die Nullhypothese  Entwickle im Sachzusammenhang eine Entscheidungsregel auf einem Signifikanzniveau von
Entwickle im Sachzusammenhang eine Entscheidungsregel auf einem Signifikanzniveau von 
(4 BE)
1.1
Betrachtet wird die mit  und
und  binomialverteilte Zufallsgröße
binomialverteilte Zufallsgröße  die von
die von  Würfen die Anzahl der Würfe beschreibt, bei denen die Zahl
Würfen die Anzahl der Würfe beschreibt, bei denen die Zahl  fällt.
fällt.
Es folgt:
Es folgt:
1.2.1
Die Augensummen  bzw.
bzw.  lassen sich in genau vier Würfen nur erreichen, wenn man nur Zweien bzw. nur Einsen würfelt. Die Wahrscheinlichkeit für eine
lassen sich in genau vier Würfen nur erreichen, wenn man nur Zweien bzw. nur Einsen würfelt. Die Wahrscheinlichkeit für eine  ist mit
ist mit  in jedem Wurf größer als die Wahrscheinlichkeit von
in jedem Wurf größer als die Wahrscheinlichkeit von  für eine
für eine 
Die Augensumme hat somit aufgrund der Unabhängigkeit der Würfe voneinander eine höhere Wahrscheinlichkeit als die Augensumme
hat somit aufgrund der Unabhängigkeit der Würfe voneinander eine höhere Wahrscheinlichkeit als die Augensumme 
Die Augensumme
1.2.2
Damit die Summe der geworfenen Zahlen in vier Würfen mindestens  beträgt, darf höchstens einmal die Zahl
beträgt, darf höchstens einmal die Zahl  geworfen werden. Es folgt:
Bei jedem Spiel beträgt die Wahrscheinlichkeit für einen Hauptpreis somit
geworfen werden. Es folgt:
Bei jedem Spiel beträgt die Wahrscheinlichkeit für einen Hauptpreis somit  Dies entspricht im Mittel jedem zwanzigsten Spiel, bei dem ein Hauptpreis vergeben wird.
Dies entspricht im Mittel jedem zwanzigsten Spiel, bei dem ein Hauptpreis vergeben wird.
1.2.3
Aufgrund der Pfadregeln müssen sich alle Wahrscheinlichkeiten für die möglichen Spielausgänge nach vier Würfen als Bruch mit dem Nenner  darstellen lassen. Da
darstellen lassen. Da  gilt, muss wie folgt erweitert werden:
gilt, muss wie folgt erweitert werden:





 ist die Wahrscheinlichkeit dafür, dass in einem Wurf die Zahl
ist die Wahrscheinlichkeit dafür, dass in einem Wurf die Zahl  fällt. Aufgrund der Pfadmultiplikationsregel ist
fällt. Aufgrund der Pfadmultiplikationsregel ist  somit die Wahrscheinlichkeit dafür, dass in allen vier Würfen die Zahl
somit die Wahrscheinlichkeit dafür, dass in allen vier Würfen die Zahl  fällt.
fällt.
Der Trostpreis wird vergeben wenn in allen vier Würfen die Zahl fällt.
fällt.
Der Trostpreis wird vergeben wenn in allen vier Würfen die Zahl
1.2.4
Bei einem Bernoulli-Experiment gibt es lediglich zwei mögliche Ausgänge des Experimentes. Hier fällt beim einmaligen Würfeln entweder die Zahl  oder die Zahl
oder die Zahl  damit handelt es sich beim einmaligen Werfen des Spielwürfels um ein Bernoulli-Experiment.
damit handelt es sich beim einmaligen Werfen des Spielwürfels um ein Bernoulli-Experiment.
Aussage ist also richtig.
ist also richtig.
Aussage
Da es hier noch einen dritten möglichen Ausgang gibt, nämlich, dass kein Preis vergeben wird, handelt es sich bei den einzelnen Durchgängen nicht um Bernoulli-Versuche und somit insgesamt auch nicht um eine Bernoulli-Kette.
Die Aussage ist damit nicht richtig.
ist damit nicht richtig.
Die Aussage
2.1
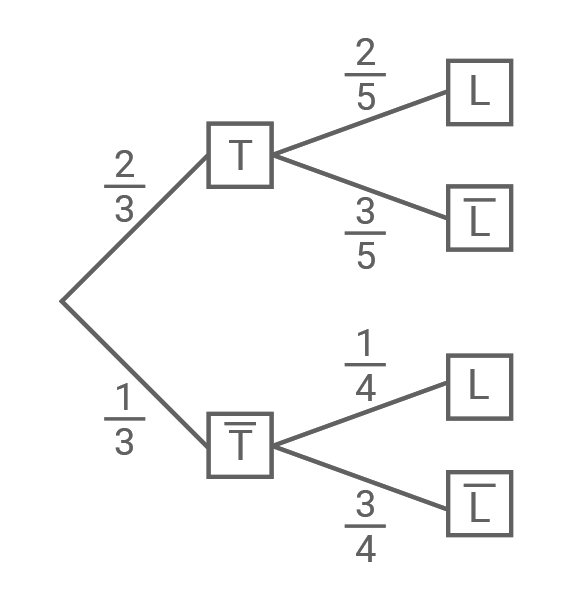
2.2
2.3
Mit dem Satz von Bayes folgt:
Mit einer Wahrscheinlichkeit von ca.  handelt es sich bei einer gekauften Light-Variante um Nassfutter.
handelt es sich bei einer gekauften Light-Variante um Nassfutter.
2.4
Entscheidungsregel entwickeln
Betrachtet wird die Zufallsgröße  die unter
die unter  zufällig ausgewählten Käufern die Anzahl derer beschreibt, die sich für Trockenfutter entscheiden.
zufällig ausgewählten Käufern die Anzahl derer beschreibt, die sich für Trockenfutter entscheiden.
Gilt die Nullhypothese, so kann im Extremfall als binomialvereteilt mit
im Extremfall als binomialvereteilt mit  und
und  angenommen werden.
Durch Umformen folgt:
Mit Hilfe einer geeigneten Tabelle oder dem Taschenrechner folgt:
angenommen werden.
Durch Umformen folgt:
Mit Hilfe einer geeigneten Tabelle oder dem Taschenrechner folgt:
 und
und  Das kleinste
Das kleinste  für das die angegebene Gleichung entsprechend des Signifikanzniveaus von
für das die angegebene Gleichung entsprechend des Signifikanzniveaus von  erfüllt ist, beträgt also
erfüllt ist, beträgt also  Wird in der Stichprobe festgestellt, dass mehr als
Wird in der Stichprobe festgestellt, dass mehr als  Käufer Trockenfutter kaufen, kann davon ausgegangen werden, dass sich der Anteil des verkauften Trockenfutters erhöht hat und die Bestellmengen für Trockenfutter erhöhen sich ebenfalls. Andernfalls kann nicht von einer erhöhten Verkaufszahl ausgegangen werden und die Bestellmengen erhöhen sich nicht.
Käufer Trockenfutter kaufen, kann davon ausgegangen werden, dass sich der Anteil des verkauften Trockenfutters erhöht hat und die Bestellmengen für Trockenfutter erhöhen sich ebenfalls. Andernfalls kann nicht von einer erhöhten Verkaufszahl ausgegangen werden und die Bestellmengen erhöhen sich nicht.
Gilt die Nullhypothese, so kann