B2 – Analysis

Abbildung 1 zeigt den Graphen der in $\mathbb R$ definierten Funktion $f$ mit $f(x)=(2-x)\cdot \mathrm e^x.$

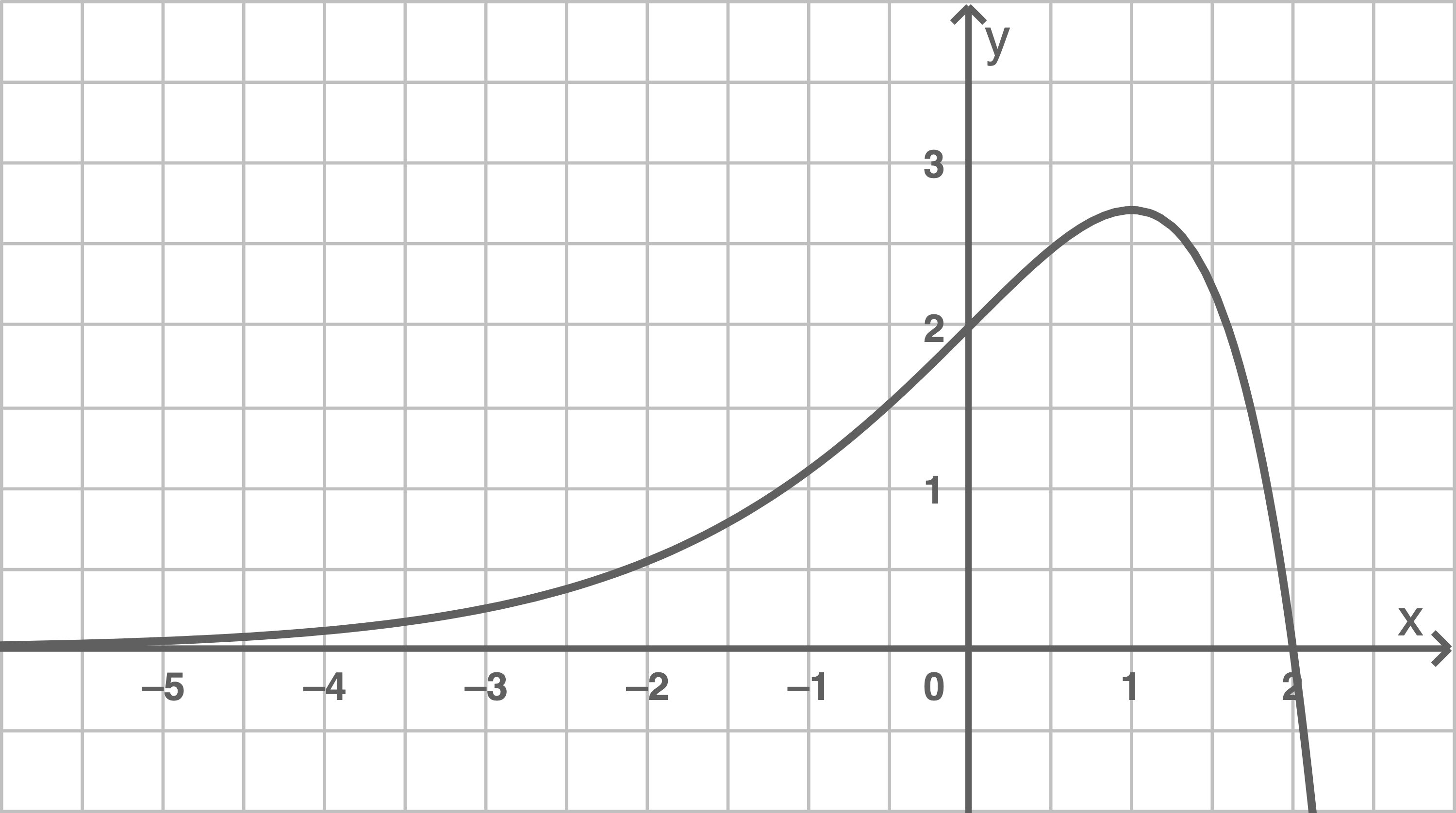
Abbildung 1

1.1

Gib die Nullstelle von $f$ sowie das Verhalten von $f$ für $x \rightarrow -\infty$ und für $x\rightarrow +\infty$ an.

(3 BE)

1.2

Berechne nur anhand der notwendigen Bedingung die Koordinaten des Hochpunkts des Graphen von $f.$

(4 BE)

1.3

Begründe mithilfe geeigneter Eintragungen in Abbildung 1 geometrisch, dass der Wert des Terms $\frac{1}{2}\cdot \mathrm e\cdot 4$ ein Näherungswert für das Integral $\displaystyle\int_{-3}^{1}f(x)\;\mathrm dx$ ist.

(3 BE)

1.4

Die in $\mathbb R$ definierte Funktion $F$ mit $F(x)=(3-x)\cdot \mathrm e^x$ ist eine Stammfunktion von $f.$

Berechne den exakten Wert des Integrals $\displaystyle\int_{-3}^{1}f(x)\;\mathrm dx$ sowie die prozentuale Abweichung des Näherungswertes $\frac{1}{2}\cdot \mathrm e\cdot 4$ vom exakten Wert.

(5 BE)

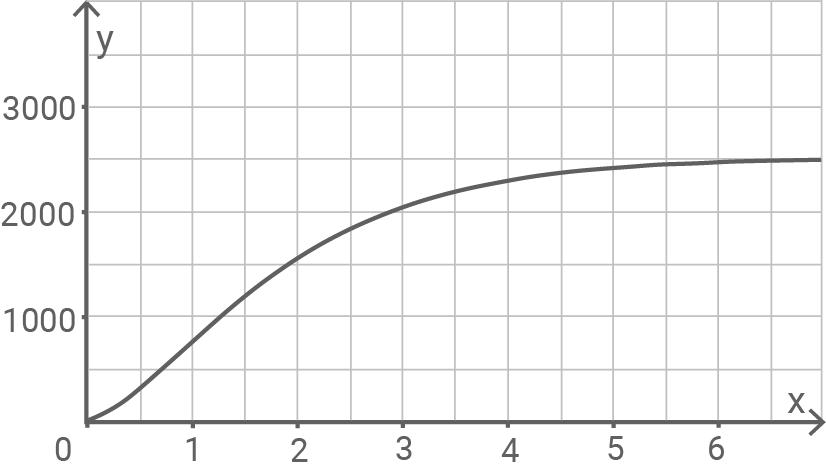
Auf einer Internetseite wird an einem bestimmten Tag um 12:00 Uhr ein Beitrag veröffentlicht. Die Anzahl der für diesen Beitrag abgegebenen Likes wird mithilfe der in $\mathbb R_0^+$ definierten Funktion $a$ beschrieben, deren Graph in Abbildung 2 dargestellt ist.

Dabei bezeichnet $x$ die seit 12:00 Uhr vergangene Zeit in Stunden und $a(x)$ die Anzahl der seit 12:00 Uhr abgegebenen Likes.

2.1

Beschreibe den Verlauf des Graphen von $a$ im Sachzusammenhang.

(2 BE)

2.2

Bestimme die Anzahl der von 14:00 Uhr bis 16:00 Uhr durchschnittlich pro Stunde abgegebenen Likes.

(3 BE)

2.3

Betrachtet wird die Gleichung $a(x + 3) = a(x) + 1000,$ die im Bereich $x\gt 0$ genau eine Lösung hat.

Abbildung 2

Ermittle die Lösung der Gleichung grafisch in Abbildung 2. Interpretiere die Gleichung im Sachzusammenhang.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Aus der Abbildung lässt sich ablesen, dass die Funktion bei $x=2$ die $x$ -Achse schneidet. Die Nullstelle beträgt daher $x=2.$

Zudem gilt:

$\lim\limits_{x\to-\infty}f(x)=0$

$\lim\limits_{x\to+\infty}f(x)=-\infty$

1.2

Für die erste Ableitung von $f$ folgt mit der Produktregel:

$\(f$ $=(1-x)\cdot \mathrm e^x$

Mit der notwendingen Bedingung $\(f$ für Extrempunkte folgt:

$\(\begin{array}[t]{rlll} f$

Da stets $\mathrm e^x\neq0$ gilt, folgt mit dem Satz des Nullprodukts:

$\begin{array}[t]{rlll} 1-x&=&0 &\mid\;+x \\[5pt] 1&=&x \end{array}$

Einsetzen in $f(x)$ liefert:

$f(1)=(2-1)\cdot\mathrm e^1=\mathrm e$

Der Hochpunkt besitzt somit die Koordinaten $H(1\mid \mathrm e).$

1.3

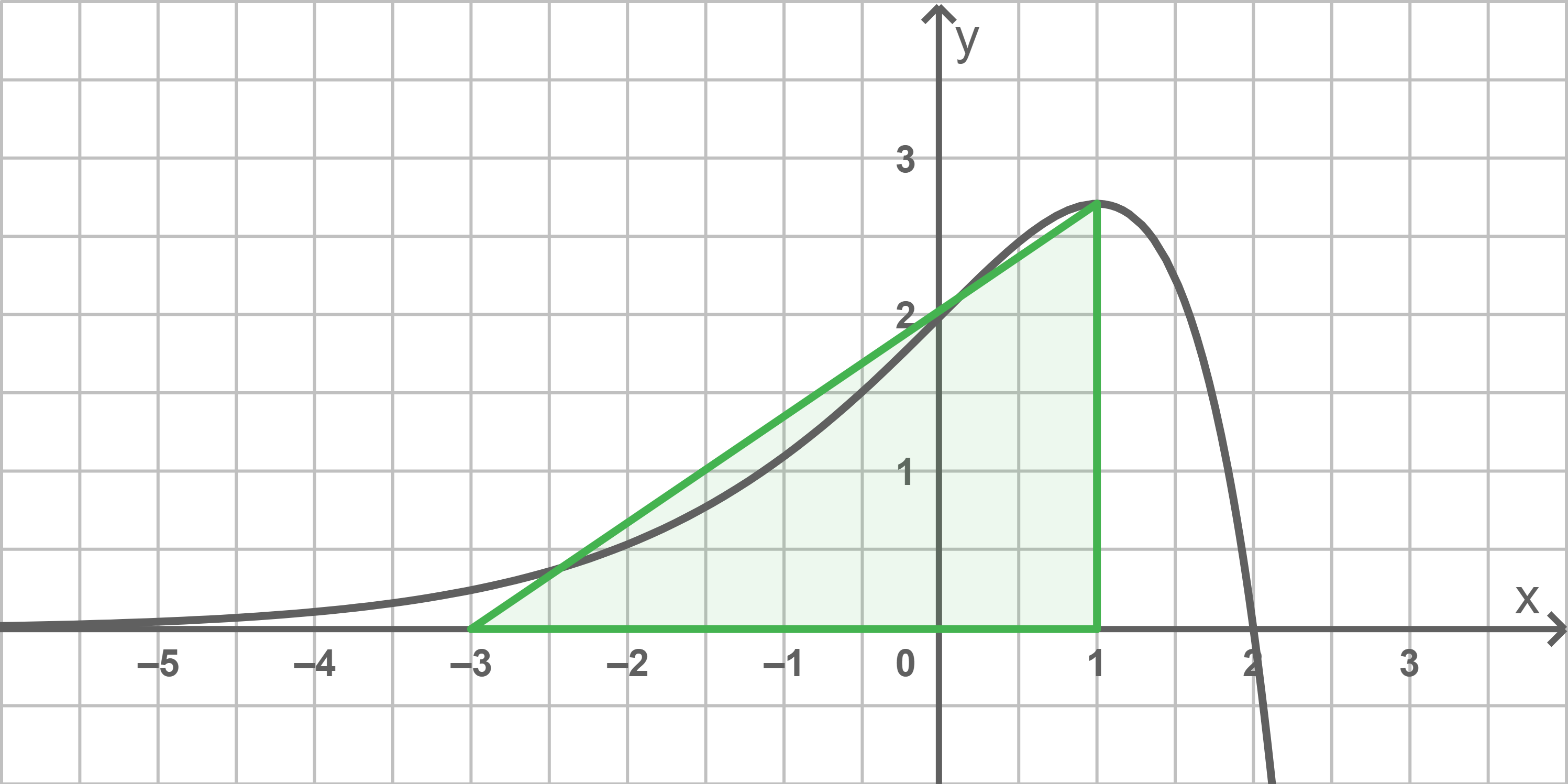
Anhand des eingezeichneten Dreiecks mit den Seitenlängen $4$ und $\mathrm e$ wird deutlich, dass der Inhalt der Fläche, die der Graph von $f$ mit der $x$ -Achse und den Geraden mit den Gleichungen $x =-3$ und $x=1$ einschließt, näherungsweise mit dem Term aus der Aufgabenstellung übereinstimmt.

1.4

Rechenweg anzeigen

$\displaystyle\int_{-3}^{1}f(x)\;\mathrm dx = 2\mathrm e-\dfrac{6}{\mathrm e^3}$

Für die prozentuale Abweichung gilt damit:

$\dfrac{\frac{1}{2}\cdot \mathrm e\cdot 4-\left(2\mathrm e-\frac{6}{\mathrm e^3}\right)}{2\mathrm e-\frac{6}{\mathrm e^3}}\approx 6\,\%$

2.1

Die Anzahl der seit der Veröffentlichung des Beitrags abgegebenen Likes nimmt immer mehr zu, aber steigt mit der Zeit immer langsamer und nähert sich auf lange Sicht $2500$ Likes an.

2.2

$\dfrac{a(4)-a(2)}{4-2}\approx \dfrac{2300-1500}{2}=400$

In der Zeit von 14:00 Uhr bis 16:00 Uhr werden durchschnittlich $400$ Like pro Stunde abgegeben.

2.3

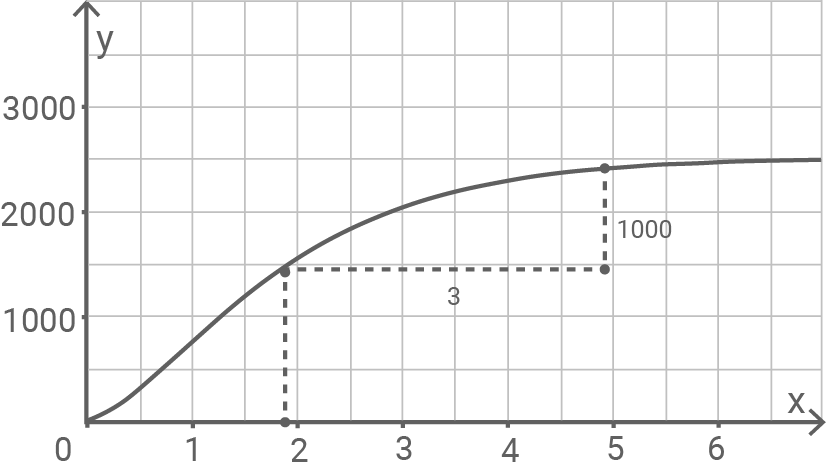
Da die gestrichelte Linie bei ca. $x=1,9$ auf die $x$ -Achse trifft, ist das die gesuchte Lösung.

Die Gleichung liefert denjenigen Zeitpunkt, zu dem die Anzahl der für den Beitrag abgegebenen Likes um $1000$ kleiner ist als die Anzahl der Likes drei Stunden später.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?