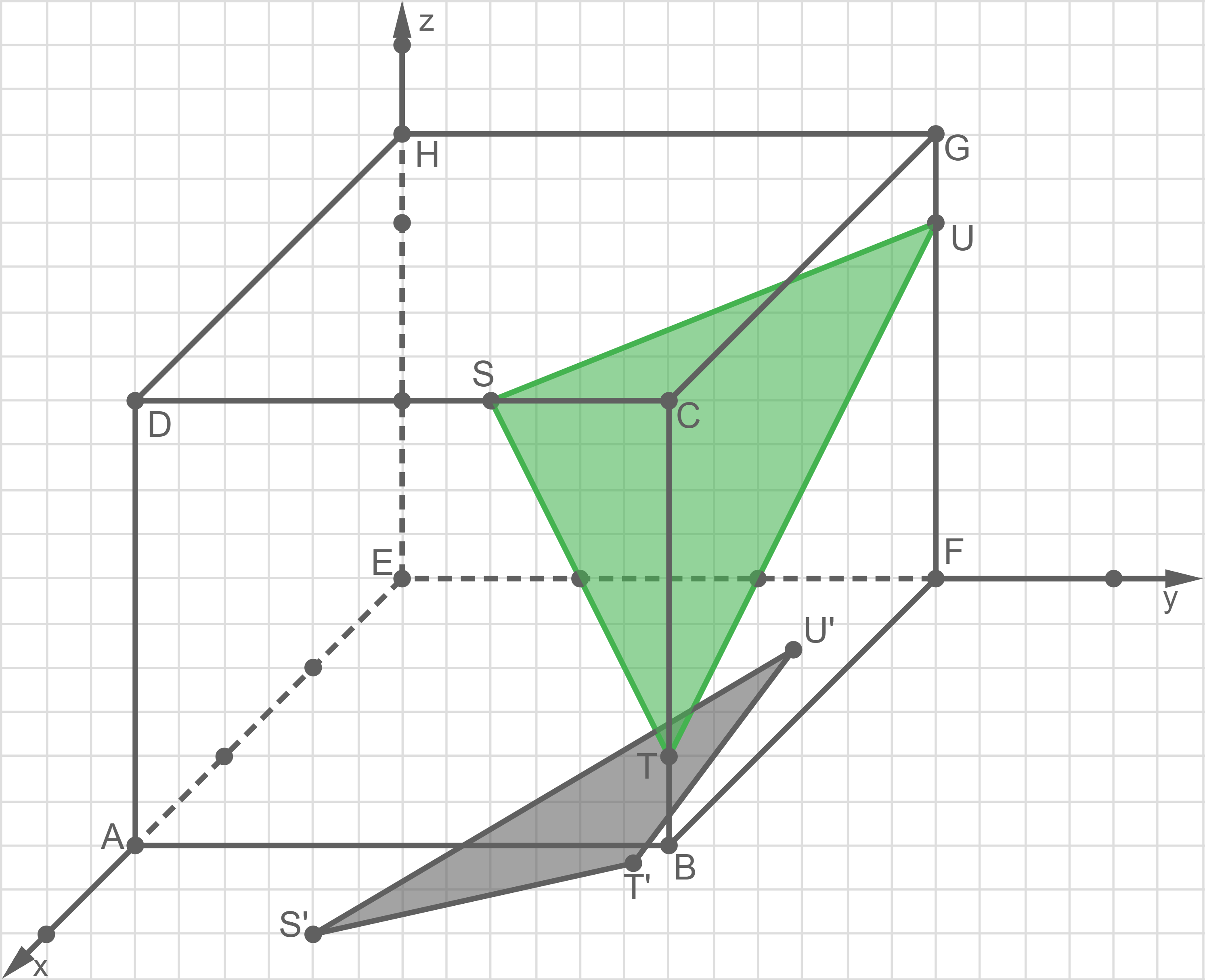
B1 - Analytische Geometrie
Gegeben ist das im Material dargestellte quaderförmige Holzgerüst mit quadratischer Grundfläche mit einer Länge und einer Breite von jeweils  und einer Höhe von
und einer Höhe von  . Als Sonnen- und Sichtschutz wird ein dreieckiges Sonnensegel in den Punkten
. Als Sonnen- und Sichtschutz wird ein dreieckiges Sonnensegel in den Punkten 
 und
und  befestigt. Der Flächeninhalt des Sonnensegels beträgt
befestigt. Der Flächeninhalt des Sonnensegels beträgt 
1
Gib die Koordinaten der Eckpunkte des Holzgerüstes an. Die Pfostendicke bleibt dabei unberücksichtigt.
(4 BE)
1.2
Zeichne das Sonnensegel in die Abbildung im Material und berechne eine Koordinatengleichung der Sonnensegelebene 
![\([\text{zur Kontrolle}: E: x + 4y +2z=16]\)](https://www.schullv.de/resources/formulas/deffb9acc9d16a0a08e500288bd4748fe951c140158308c7fb7547453f3ed023_light.svg)
(7 BE)
1.3
Durch das Sonnensegel wird die Höhe eingeschränkt. Damit man den Raum noch großzügig nutzen kann, soll die Stehhöhe über dem Punkt  noch
noch  betragen. Prüfe, ob durch die Befestigung des Sonnensegels die Stehhöhe über dem Punkt
betragen. Prüfe, ob durch die Befestigung des Sonnensegels die Stehhöhe über dem Punkt  beeinträchtigt wird.
beeinträchtigt wird.
(4 BE)
1.4
Bestimme den Winkel zwischen der Sonnensegelebene und der Dachebene 
(3 BE)
2
Bei starkem Wind beginnt das Sonnensegel zu flattern. Um die Bewegung des Sonnensegels einzuschränken, wird eine zur Dreiecksfläche orthogonale Verbindung zum Eckpunkt  konzipiert.
konzipiert.
2.1
Bestimme die Länge dieses Verbindungsstücks unter der modellhaften Annahme, dass das Sonnensegel so gespannt wurde, dass es nicht durchhängt.
![\(\left[ \text{zur Kontrolle: } d \approx 0,87\;\text{m}\right]\)](https://www.schullv.de/resources/formulas/fb35b36d0c2b174ec7fffcd46ef86a385918f42c48476d9332948d2768da2939_light.svg)
(4 BE)
2.2
Zu künstlerischen Zwecken sollen innerhalb des Holzgerüsts drei weitere dreieckige Tücher gespannt werden, die jeweils eine Seitenkante des vorhandenen Sonnensegels mit dem Eckpunkt  verbinden. Berechne, wie viel Prozent des Raumes innerhalb des Holzgerüstes der entstehende Körper einnimmt.
verbinden. Berechne, wie viel Prozent des Raumes innerhalb des Holzgerüstes der entstehende Körper einnimmt.
(4 BE)
3
Es beginnt zu regnen. Die Regentropfen fallen dabei modellhaft geradlinig in Richtung  Durch das Sonnensegel bleibt ein Teil des Bodens trocken. Dieser trockene Teil wird durch die Punkte
Durch das Sonnensegel bleibt ein Teil des Bodens trocken. Dieser trockene Teil wird durch die Punkte 
 und
und  begrenzt. Berechne die Koordinaten von
begrenzt. Berechne die Koordinaten von  und stelle diese Fläche in deiner Zeichnung dar.
und stelle diese Fläche in deiner Zeichnung dar.
Material
(4 BE)

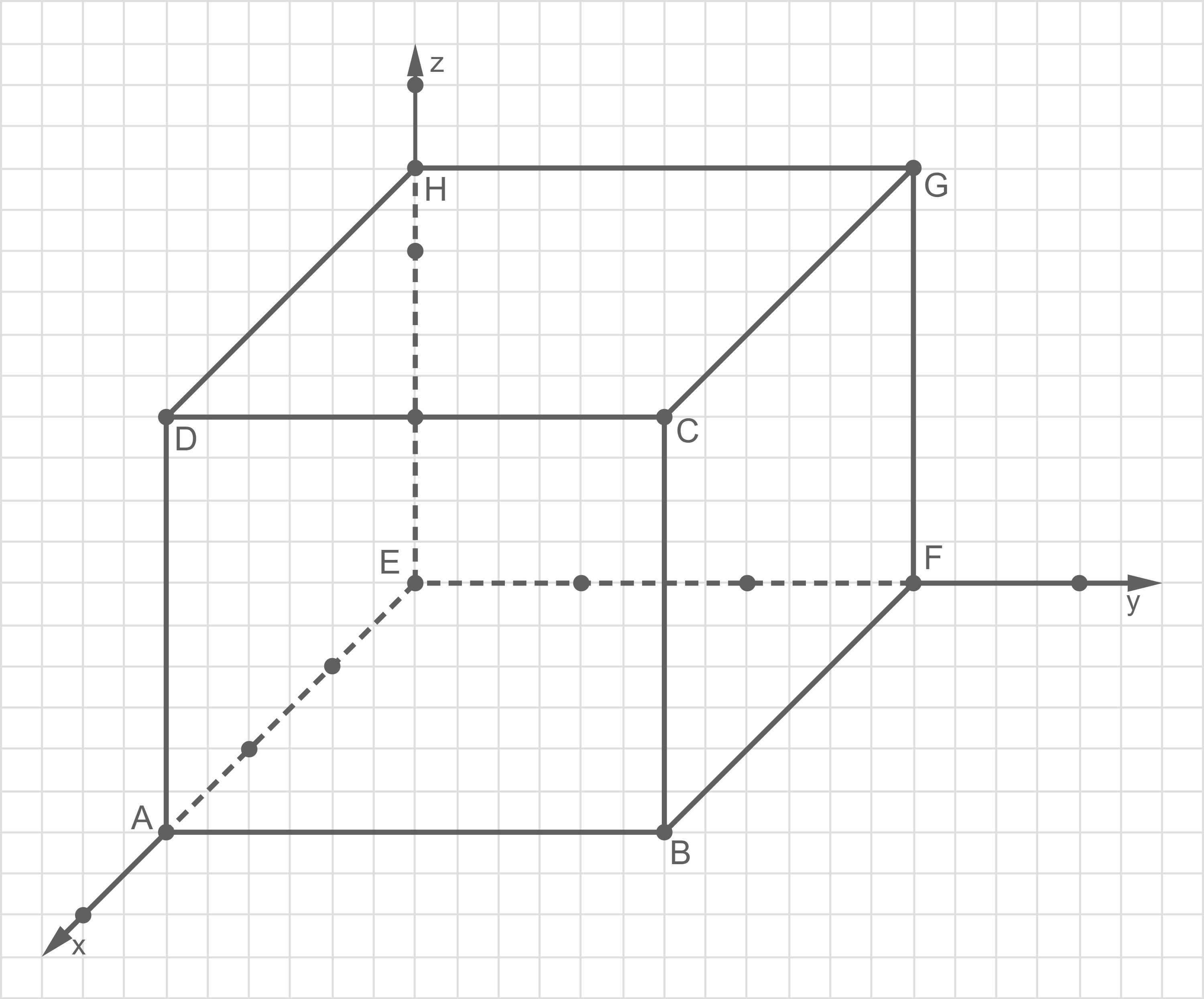
1.1
Aus der Augabenstellung folgt, dass die Länge und Breite des Holzgerüstes  beträgt und die Höhe
beträgt und die Höhe  Mit Hilfe des Koordinatensystems folgt, dass ein Meter einer Längeneinheit entspricht, sowie dass
Mit Hilfe des Koordinatensystems folgt, dass ein Meter einer Längeneinheit entspricht, sowie dass  im Ursprung liegt. Damit ergeben sich folgende Koordinaten für die Eckpunkte:
im Ursprung liegt. Damit ergeben sich folgende Koordinaten für die Eckpunkte:
![\(\begin{array}[t]{l}
A( 3 \mid 0 \mid 0) \\[5pt]
B(3 \mid 3 \mid 0) \\[5pt]
C( 3 \mid 3 \mid 2,5) \\[5pt]
D( 3 \mid 0 \mid 2,5) \\[5pt]
E( 0 \mid 0 \mid 0) \\[5pt]
F( 0 \mid 3 \mid 0) \\[5pt]
G( 0 \mid 3 \mid 2,5) \\[5pt]
H( 0 \mid 0 \mid 2,5)
\end{array}\)](https://www.schullv.de/resources/formulas/293c02da42b15061a733e62adb44d86a25dce68855cb78183b31b23fb944b908_light.svg)
1.2
Sonnensegel einzeichnen
Einzeichnen der drei gegebenen Punkte  ,
,  und
und  und Verbinden dieser liefert:
und Verbinden dieser liefert:
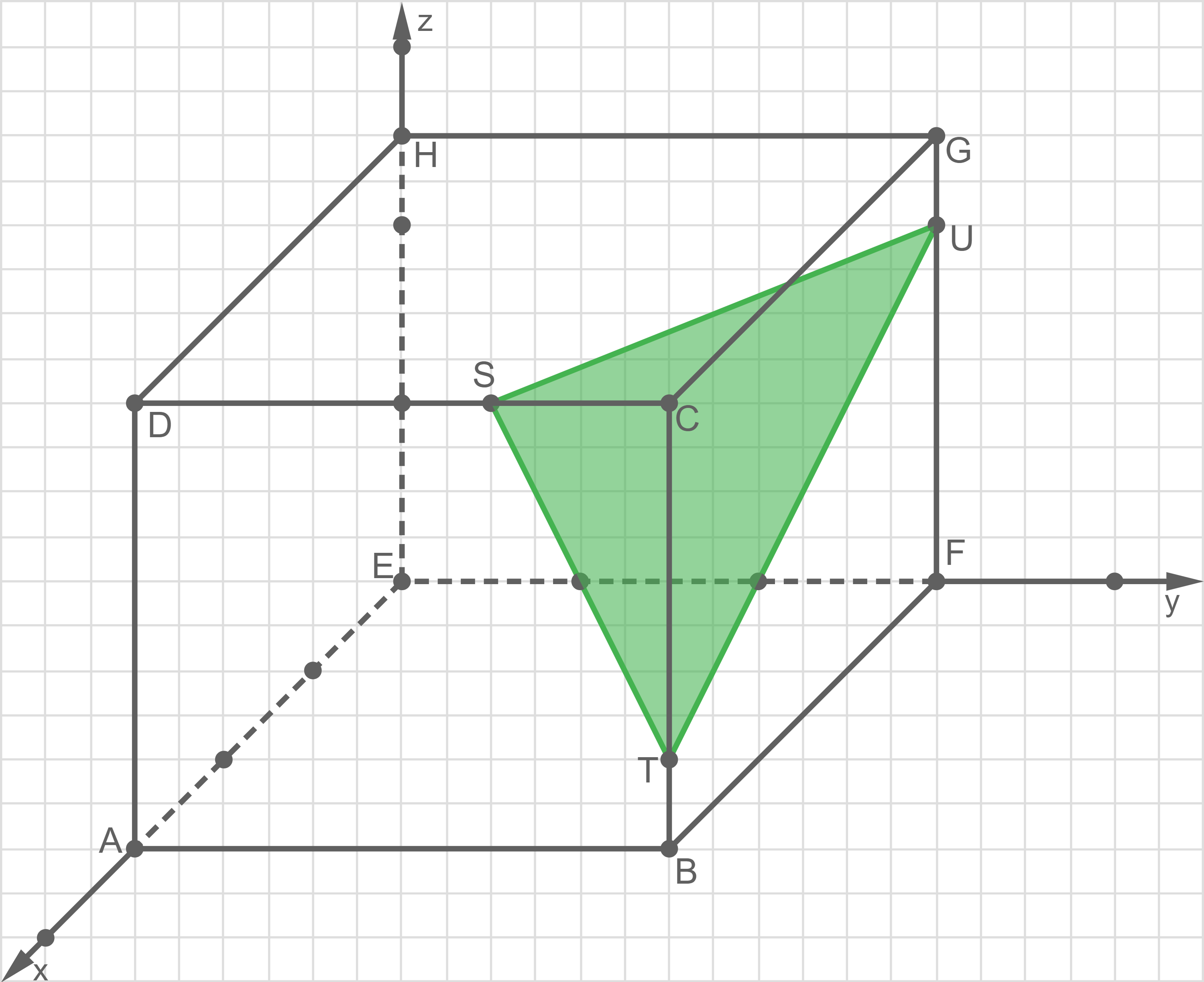 Koordinatengleichung der Sonnensegelebene
Koordinatengleichung der Sonnensegelebene  berechnen
Zwei Spannvektoren der Ebene ergeben sich wie folgt:
berechnen
Zwei Spannvektoren der Ebene ergeben sich wie folgt:











 Mit Hilfe des Kreuproduktes der beiden Stützvektoren ergibt sich für den Normalenvektor der Ebene:
Mit Hilfe des Kreuproduktes der beiden Stützvektoren ergibt sich für den Normalenvektor der Ebene:




 Einsetzen von
Einsetzen von  liefert weiter:
liefert weiter:






 Somit folgt für die allgemeine Koordinatengleichung insgesamt:
Somit folgt für die allgemeine Koordinatengleichung insgesamt:
![\(\begin{array}{rll}
E: &1,5\cdot x + 6\cdot y + 3 \cdot z =24 & \;\scriptsize \mid \; :1,5 \\[5pt]
E: &x + 4\cdot y + 2 \cdot z =16
\end{array}\)](https://www.schullv.de/resources/formulas/71d7cd3ba576a89523e85634d30f7b2fd8e5ae47739a2d781ec7a83db08fa554_light.svg)

1.3
Einsetzen der  - und
- und  -Koordinate von
-Koordinate von  in die Koordinatengleichung der Ebene
in die Koordinatengleichung der Ebene  und auflösen nach der
und auflösen nach der  -Koordinaten liefert die Höhe des Sonnensegels über dem Boden am Punkt
-Koordinaten liefert die Höhe des Sonnensegels über dem Boden am Punkt  Die geforderte Stehhöhe von
Die geforderte Stehhöhe von  wird durch das Sonnensegel somit beeinträchtigt.
wird durch das Sonnensegel somit beeinträchtigt.
1.4
1. Schritt: Normalenvektoren bestimmen
Der Normalenvekor der Sonnensegelebene  folgt direkt aus der Koordinatengleichung:
folgt direkt aus der Koordinatengleichung:
 Da die Dachebene die
Da die Dachebene die  -Ebene ist, gilt
-Ebene ist, gilt  2. Schritt: Schnittwinkel berechnen
Der Winkel zwischen Sonnensegelebene und Dachebene beträgt damit ca.
2. Schritt: Schnittwinkel berechnen
Der Winkel zwischen Sonnensegelebene und Dachebene beträgt damit ca.  .
.
2.1
Da die Länge von  durch
durch 

 gegeben ist, folgt für die Hessesche Normalform der Ebene
gegeben ist, folgt für die Hessesche Normalform der Ebene 

 Einsetzen von
Einsetzen von  liefert dann weiter:
liefert dann weiter:



 Das Verbindungsstück ist somit ca.
Das Verbindungsstück ist somit ca.  lang.
lang.
2.2
1. Schritt: Volumen des Holzgerüsts berechnen
Das Holzgerüst hat eine Länge von  , eine Breite von
, eine Breite von  und eine Höhe von
und eine Höhe von  Damit ergibt sich für das Volumen:
Damit ergibt sich für das Volumen:


![\( = 22,5 \;[\text{ m}^3]\)](https://www.schullv.de/resources/formulas/01c7a2c4a8e83eea560eb6281241f0c6a0de7db4d59abf40de288a9dffb7b12a_light.svg) 2. Schritt: Volumen des Körpers berechnen
Der gebildete Körper ist eine Pyramide mit dem vorhandenen Sonnensegel als Grundfläche und dem Punkt
2. Schritt: Volumen des Körpers berechnen
Der gebildete Körper ist eine Pyramide mit dem vorhandenen Sonnensegel als Grundfläche und dem Punkt  als Spitze. Für das Volumen der Pyramide folgt:
als Spitze. Für das Volumen der Pyramide folgt:







![\( \approx 1 \; [\text{m}^3]\)](https://www.schullv.de/resources/formulas/f8a59ee85816530d412f4c5f9a3a1f6dce7cc77bc413af513b80b90c46a0856c_light.svg) 3. Schritt: Prozentualen Anteil berechnen
3. Schritt: Prozentualen Anteil berechnen



 Damit nimmt der entstehende Körper etwa
Damit nimmt der entstehende Körper etwa  des Raumes innerhalb des Holzgerüstes ein.
des Raumes innerhalb des Holzgerüstes ein.
3
1. Schritt: Koordinaten von  berechnen
berechnen
 ist der Punkt auf dem Boden, auf dem die Regentropfen landen würden, die vom Eckpunkt
ist der Punkt auf dem Boden, auf dem die Regentropfen landen würden, die vom Eckpunkt  des Sonnensegels abgefangen werden. Mit Hilfe des Richtungsvektors
des Sonnensegels abgefangen werden. Mit Hilfe des Richtungsvektors  aus der Aufgabenstellung und dem Ortsvektor von
aus der Aufgabenstellung und dem Ortsvektor von  als Stützvektor folgt:
als Stützvektor folgt:

 2. Schritt:
2. Schritt:  berechnen
Da die
berechnen
Da die  -Koordinate von
-Koordinate von  Null ist, folgt aus der Geradengleichung von
Null ist, folgt aus der Geradengleichung von  Für die
Für die  -Koordinate des gesuchten Punktes
-Koordinate des gesuchten Punktes  folgt damit:
folgt damit:




 Die
Die  -Koordinate ergibt sich zu:
-Koordinate ergibt sich zu:




 Die Koordinaten des Punktes
Die Koordinaten des Punktes  sind damit gegeben durch
sind damit gegeben durch  3. Schritt: Fläche einzeichnen
3. Schritt: Fläche einzeichnen