B1 – Analysis

In der Nähe einer Schule soll ein Bike- und Skatepark entstehen. Damit die verwendeten Elemente belastbar sind, werden sie aus Leichtbeton gefertigt.

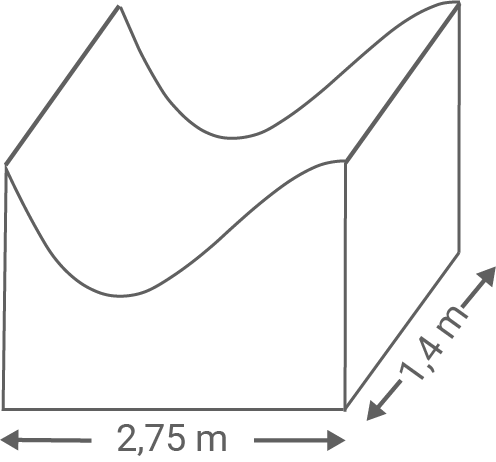
Ein $2,75\;\text{m}$ breites und $1,4\;\text{m}$ tiefes Element (siehe Abbildungen 1.1 und 1.2) wird in einer Betonfabrik vorgefertigt und soll dann mithilfe eines LKWs transportiert werden.

Schrägansicht:

Abbildung 1.1

Seitenansicht:

Abbildung 1.2

In einem mathematischen Modell kann die obere Profillinie des Elements durch den im Intervall $[0;2,75]$ gelegenen Ausschnitt des Graphen der Funktion $f$ mit $f(x) = -0,24x^3 +1,44x^2-2,16x +1,76$ ( $x$ und $f(x)$ in Metern) beschrieben werden (Abbildung 2).

Graph der Funktion $\boldsymbol{f}$

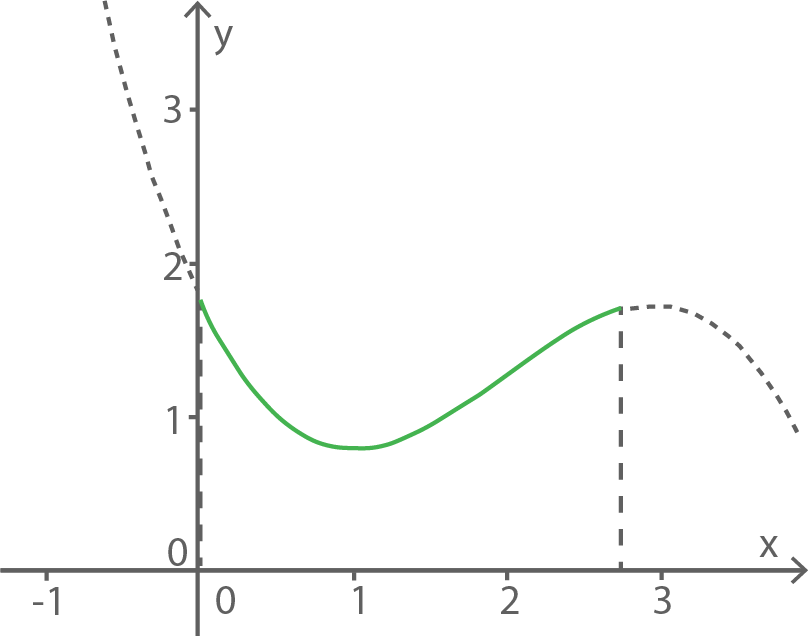
Abbildung 2

Betrachtet man eine zur $x$ -Achse orthogonale Schnittfläche des mathematischen Körpers, der das Element beschreibt, so handelt es sich stets um ein Rechteck.

1.1

Berechne den kleinsten und den größten Funktionswert der Funktion $f$ im Intervall $[0; 2,75].$ Die Funktionsgleichung der zweiten Ableitungsfunktion $\(f$ kann ohne Herleitung verwendet werden.

(6 BE)

1.2

Zeige, dass die Funktion $f$ bei $x = 2$ eine Wendestelle besitzt. Für den Winkel $\alpha$ gilt: $\(\tan(\alpha) = f$

Bestimme $\alpha$ und deuten Sie den Winkel im Sachzusammenhang.

(4 BE)

1.3

Berechne den Flächeninhalt $A$ des Elements in der Seitenansicht (siehe Abbildung 1).

[zur Kontrolle: $A \approx 3,2235\;\text{m}^2$ ]

(4 BE)

1.4

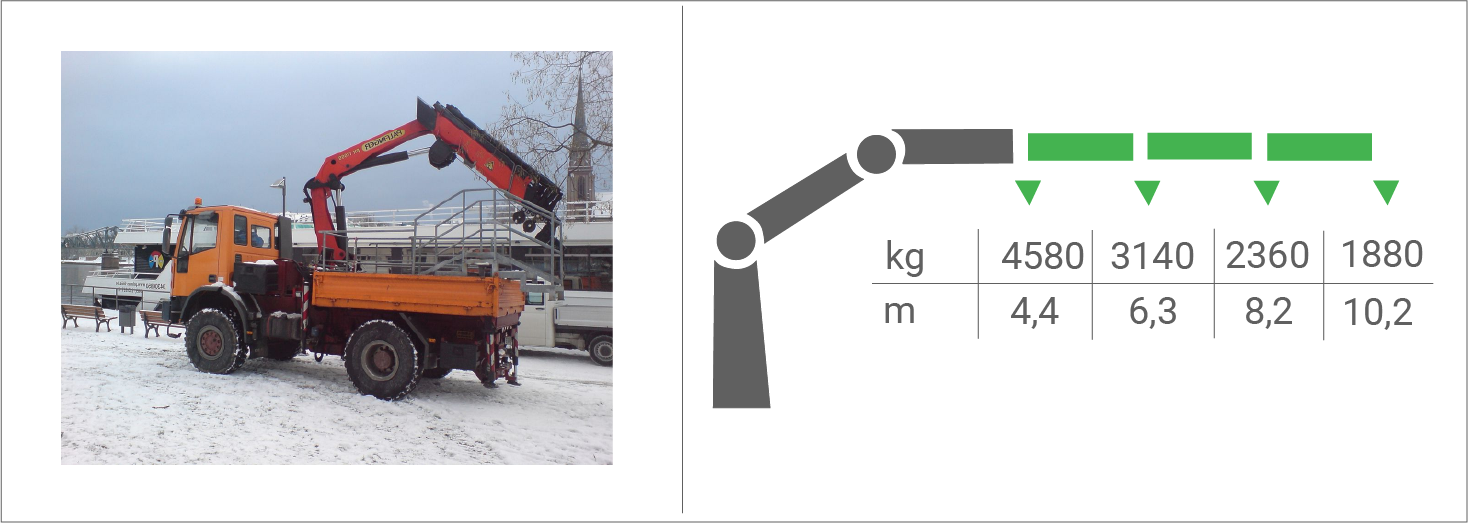
Für den Transport des Elements wird ein LKW mit integriertem Ladekran verwendet (siehe Abbildung 3). Die maximale Masse, welche der Ladekran heben kann, bezeichnet man als maximale Hubkapazität. Diese ist davon abhängig, in welcher Entfernung von der Ladefläche ein Element gehoben werden muss. In Abbildung 3 sind hierzu einige Wertepaare angegeben.

Darstellung des Ladekrans sowie der entfernungsabhängigen Hubkapazität

Abbildung 3

Bestimme das Volumen und die Masse des betrachteten Elements in $\text{kg},$ wenn bekannt ist, dass $1\;\text{m}^3$ des verwendeten Leichtbetons $695\;\text{kg}$ wiegt.

Entscheide begründet, bis zu welcher näherungsweisen Entfernung von der Ladefläche das Element mithilfe des Ladekrans gehoben werden kann.

(3 BE)

Im Folgenden soll für das Volumen des Elements der gerundete Wert $4,5\;\text{m}^3$ verwendet werden.

1.5

Zum Schutz während des Transports werden an allen Seitenwänden des Elements Platten mit einer Höhe von jeweils $2\;\text{m}$ angebracht, sodass ein nach oben offener Quader entsteht.

1.5.1

Aufgrund mehrerer Unwetter sammelt sich auf dem Element bis zur Oberkante der angebrachten Platten Wasser.

Bestimme das Volumen $W$ des Wassers, das sich so angesammelt hat, in $\text{m}^3.$

(2 BE)

1.5.2

Durch ein kleines Bohrloch in einer der Platten, das sich im Modell in der Nähe des Tiefpunkts des Graphen von $f$ befindet, wird zur Gewichtsreduktion Wasser abgelassen.

Die Abflussrate des Wassers kann innerhalb der ersten Minuten mithilfe der Funktion $v$ mit $v(t)=\frac{2}{t+2}$ beschrieben werden ( $t$ in Minuten ab dem Zeitpunkt, zu dem das Ablassen des Wassers beginnt; $v(t)$ in $\text{m}^3$ pro Minute).

Erläutere unter Bezugnahme auf das Volumen $W$ des Wassers die Bedeutung der folgenden Aussage im Sachzusammenhang: $\displaystyle\int_{0}^{k}v(t)\;\mathrm dt=W$ $\Rightarrow$ $k\approx 7,9 \;\ (k \gt 0)$

(2 BE)

2.1

Gegeben ist eine weitere Funktion $g$ mit $g(x)=a\cdot x^3+b\cdot x^2+c\cdot x+d$ ( $a,b,c$ und $d$ seien dabei reelle Parameter).

Der Graph der Funktion $g$ soll punktsymmetrisch zum oberhalb des Ursprungs gelegenen Punkts $P(0\mid 1)$ verlaufen und $g$ eine Funktion dritten Grades sein.

Gib die Bedingungen an, welche die Parameter $a, b, c$ und $d$ erfüllen müssen.

(2 BE)

2.2

Für die Funktion $f$ aus Aufgabe 1 gilt für jede beliebige reelle Zahl $h$ die folgende Gleichung:

$f(2)-f(2-h)=f(2+h)-f(2)$

Beschreibe die geometrische Bedeutung dieser Gleichung.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Bedingung für Extrempunkte: $\(f$

$\(f$

Nullsetzen liefert:

$\(\begin{array}[t]{rlll} f$

Mit der $pq$ -Formel folgt:

$\begin{array}[t]{rlll} x_{1;2}&=&2\pm\sqrt{4-3} \\[5pt] x_1&=&3 \\[5pt] x_2&=&1 \end{array}$

Da $x_2$ außerhalb des betrachteten Intervalls liegt, ist hier nur $x_1$ relevant:

$\(f$

Somit besitzt $f$ bei $x_1$ ein Minimum.

Für den Funktionswert am Minimum gilt:

Rechenweg anzeigen

$f(1)=0,8$

Für die Funktionswerte an den Intervallgrenzen gilt:

Rechenweg anzeigen

$f(0)=1,76$

Rechenweg anzeigen

$f(2,75)\approx1,72$

Der größte Funktionswert im betrachteten Intervall ist somit $f(0)=1,76$ und der kleinste Funktionswert $f(1)=0,8.$

1.2

Für die dritte Ableitung gilt $\(f$

Da $\(f$ und $\(f$ gilt, besitzt die Funktion $f$ bei $x=2$ eine Wendestelle.

Für $\(f$ gilt:

$\(\begin{array}[t]{rlll} f$

Damit folgt:

$\begin{array}[t]{rlll} \tan(\alpha)&=&0,72 \\[5pt] \alpha&\approx&35,75^\circ \end{array}$

Der Winkel $\alpha$ beschreibt den maximalen Steigungswinkel der Profillinie und beträgt ca. $35,75^\circ.$

1.3

Rechenweg anzeigen

$A\approx3,32\text{m^2}$

1.4

Volumen: $3,22\cdot 1,4=4,51\;[\text{m}^3]$

Masse: $4,51\cdot 695\approx 3134,45\;\text{kg}$

Das Element kann bis zu einer Entfernung von ca. $6,3\;\text{m}$ von der Ladefläche gehoben werden, da die Masse des Elements etwas weniger als $3140\;\text{kg}$ beträgt.