A1 - Analysis

In einem Fachgeschäft wird eine Werbeaktion für ein spezielles Smartphone durchgeführt. Die täglichen Verkaufszahlen lassen sich näherungsweise durch die Funktion $g$ mit $g(t)=\ 30\cdot t \cdot \mathrm{e}^{-0,1 \cdot t}$ beschreiben. Hierbei steht $t$ für die Zeit in Tagen nach Beginn der Werbeaktion und $g(t)$ für die Anzahl der verkauften Smartphones pro Tag.

Berechne den Zeitpunkt, an dem die meisten Smartphones (pro Tag) verkauft werden, und bestimme die ungefähre Anzahl der verkauften Geräte an diesem Tag.

(8 BE)

Im Folgenden werden die jährlichen Verkaufszahlen von Smartphones in einem Land mit 80 Millionen Einwohnern in den Jahren 2008 bis 2013 betrachtet. Hierzu wird das Jahr 2008 als Startzeitpunkt ( $t=0$ ) angenommen. Der Wert $t$ beschreibt die Zeit in Jahren nach 2008. Für das Jahr 2012 gilt beispielsweise $t=4$ .

Die Entwicklung der Verkaufszahlen von Smartphones in den Jahren 2008 bis 2013 ist in folgender Tabelle angegeben:

Jahr	$\color{#fff}{t}$ in Jahren nach 2008	Verkaufszahlen in Millionen Stück pro Jahr
$2008$	$0$	$5,00$
$2009$	$1$	$7,10$
$2010$	$2$	$10,00$
$2011$	$3$	$14,20$
$2012$	$4$	$20,10$
$2013$	$5$	$28,60$

2.1

Die Daten aus der Tabelle sollen als Säulendiagramm dargestellt werden. Zeichne die fehlenden Säulen in die folgende Abbildung.

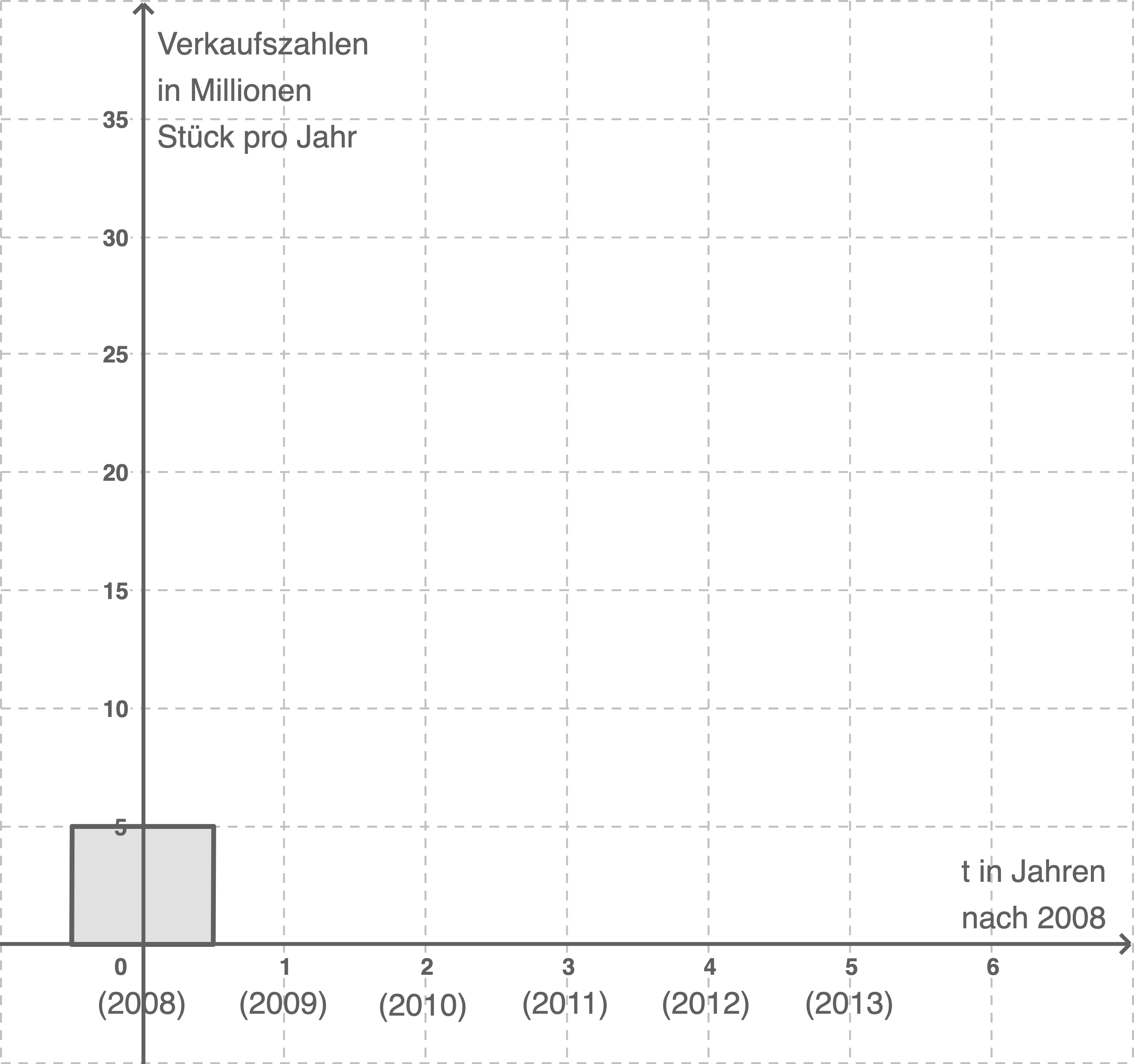
Saeulendiagramm Verkaufszahlen Smartphone Hessen Abi 2016

(4 BE)

2.2

Zeige, dass die Entwicklung der Verkaufszahlen von Smartphones in diesem Zeitraum annähernd exponentiell verlief, und bestimme die Gleichung einer Exponentialfunktion $v$ der Form $v(t)=\ a \cdot b^t$ , welche die Verkaufszahlen von Smartphones modelliert ( $t$ : Zeit in Jahren nach 2008, $v(t)$ : Anzahl verkaufter Smartphones in Millionen Stück pro Jahr).

(5 BE)

Im Folgenden wird die Entwicklung der jährlichen Verkaufszahlen der Smartphones durch die Funktion $f$ mit $f(t)=\ 5 \cdot \mathrm{e}^{0,351 \cdot t}$ modelliert ( $t$ : Zeit in Jahren nach 2008, $f(t)$ : Anzahl verkaufter Smartphones in Millionen Stück pro Jahr).

3.1

Skizziere den Verlauf des Funktionsgraphen von $f$ im Intervall $[-0,5;5,5]$ in das Säulendiagramm aus Aufgabenteil 2.1.

(4 BE)

3.2

Berechne den Wert des Integrals $\displaystyle\int_{0}^{5}\; f(t)\;\mathrm dt$ und deute diesen im Sachzusammenhang.

(7 BE)

3.3

Bestimme unter Verwendung der Tabelle aus Aufgabe 2 die Gesamtzahl der in den Jahren 2008 bis einschließlich 2013 tatsächlich verkauften Smartphones.

Vergleiche diesen Wert mit dem Ergebnis aus Aufgabenteil 3.2 und erkläre die Abweichung.

Erläutere, wie durch Modifikation des Integrals aus Aufgabenteil 3.2 ein besseres Ergebnis erzielt werden kann, und gib eine Modifikation an.

(7 BE)

3.4

Bestimme mithilfe der Modellierungsfunktion $f$ die zu erwartenden Verkaufszahlen von Smartphones im Jahr 2030 in diesem Land.

Beurteile diesen Wert sowie die Güte der Modellierung.

(5 BE)

1. Schritt: Ableitungen bestimmen

$\(\begin{array}[t]{rll} g(t)&=& 30 \cdot t\cdot \mathrm e^{-0,1 \cdot t} &\quad \scriptsize\; \\[10pt] g‘(t)&=& 30 \cdot 1\cdot \mathrm e^{-0,1 \cdot t} - 0,1\cdot 30 \cdot t \cdot \mathrm e^{-0,1 \cdot t} \\[5pt] &=& \mathrm e^{-0,1 \cdot t}\cdot(30-3\cdot t)&\quad \scriptsize \\[10pt] g$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\begin{array}[t]{rll} g‘(t)&=&0 &\quad \scriptsize \\[5pt] \mathrm e^{-0,1 \cdot t}\cdot(30-3t) &=&0 \end{array}$

Da $\mathrm e^{-0,1 \cdot t}\neq0$ gilt, folgt mit dem Satz vom Nullprodukt:

$\begin{array}[t]{rll} 30-3t &=& 0 &\quad \scriptsize \mid\; +3t\\[5pt] 30 &=& 3t \\[5pt] 10 &=& t \end{array}$

3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} g$

Der Hochpunkt ist somit gegeben durch den Punkt $H(10\mid g(10)).$

4. Schritt: $y$ -Koordinate berechnen

$\begin{array}[t]{rll} g(10)&=& 30\cdot 10\cdot \mathrm e^{-0,1\cdot 10} \\[5pt] &\approx& 110 \end{array}$

Am 10. Tag nach Beginn der Werbeaktion werden mit ungefähr 110 Smartphones die meisten Smartphones an einem Tag verkauft.

2.1

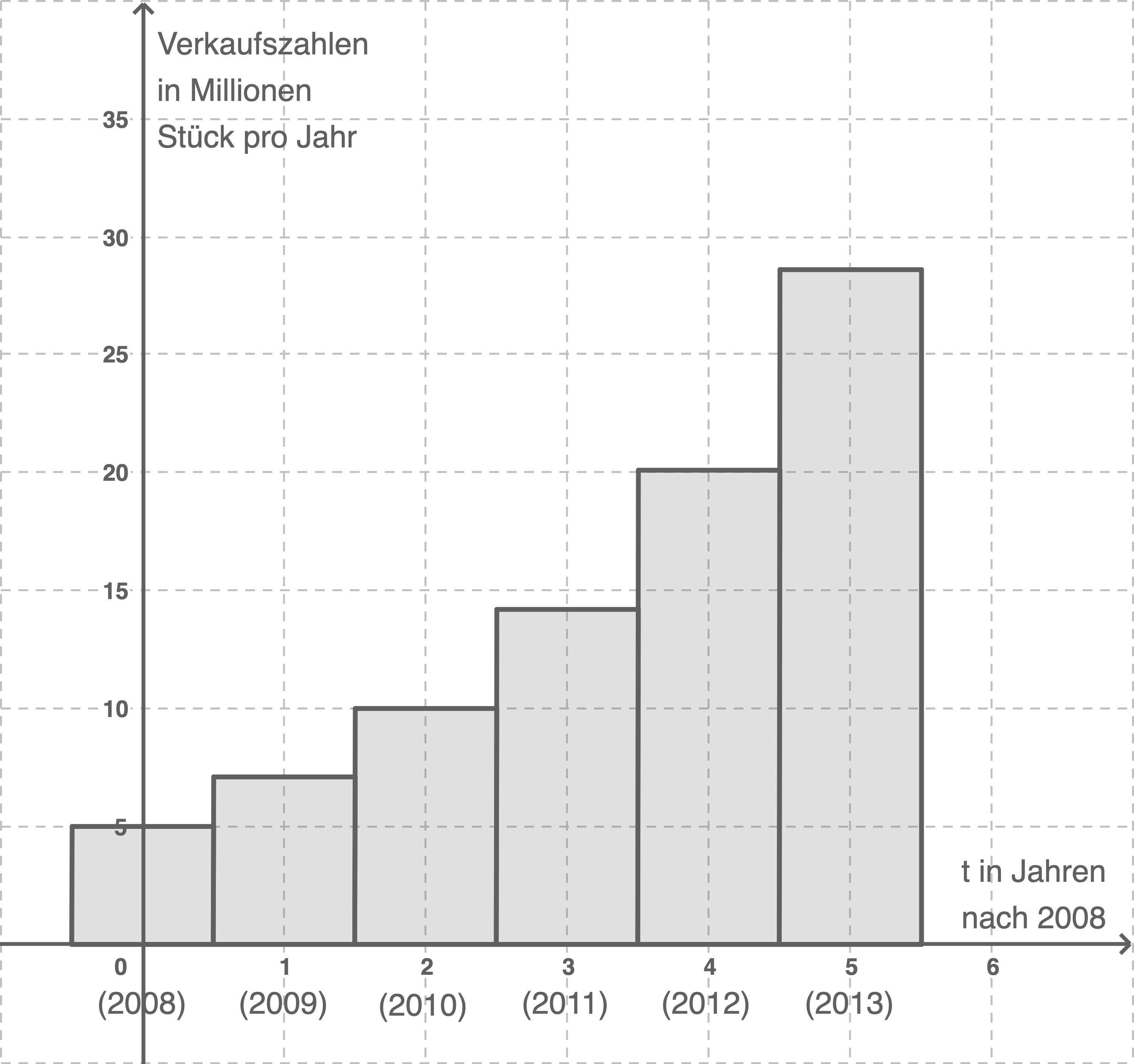
Saeulendiagramm Verkaufszahlen Smartphone Loesung Hessen Abi 2016

2.2

Exponentiellen Verlauf zeigen

Es gilt:

$\begin{array}[t]{rll} \dfrac{7,10}{5,00}&=& 1,42& &\quad \scriptsize \\[5pt] \dfrac{10,0}{7,10}&\approx& 1,41& \scriptsize \\[5pt] \dfrac{14,2}{10,0}&= & 1,42& \scriptsize \\[5pt] \dfrac{20,1}{14,2}&\approx & 1,42& \scriptsize \\[5pt] \dfrac{28,6}{20,1}&\approx& 1,42& \scriptsize \\[5pt] \end{array}$

Da sich ein annähernd konstanter Wachstumsfaktor erkennen lässt, handelt es sich hierbei um ein exponentielles Wachstum mit einem Mittelwert von $1,42.$

Gleichung bestimmen

$v(t)=a\cdot 1,42^t$

Aus der Tabelle ergibt sich:

$\begin{array}[t]{rll} v(0)&=& 5 \\[5pt] a\cdot 1,42^0&=& 5 \\[5pt] a &=& 5 \end{array}$

Somit lautet eine Gleichung der Exponentialfunktion $v$ :

$v(t)=5\cdot 1,42^t$

3.1

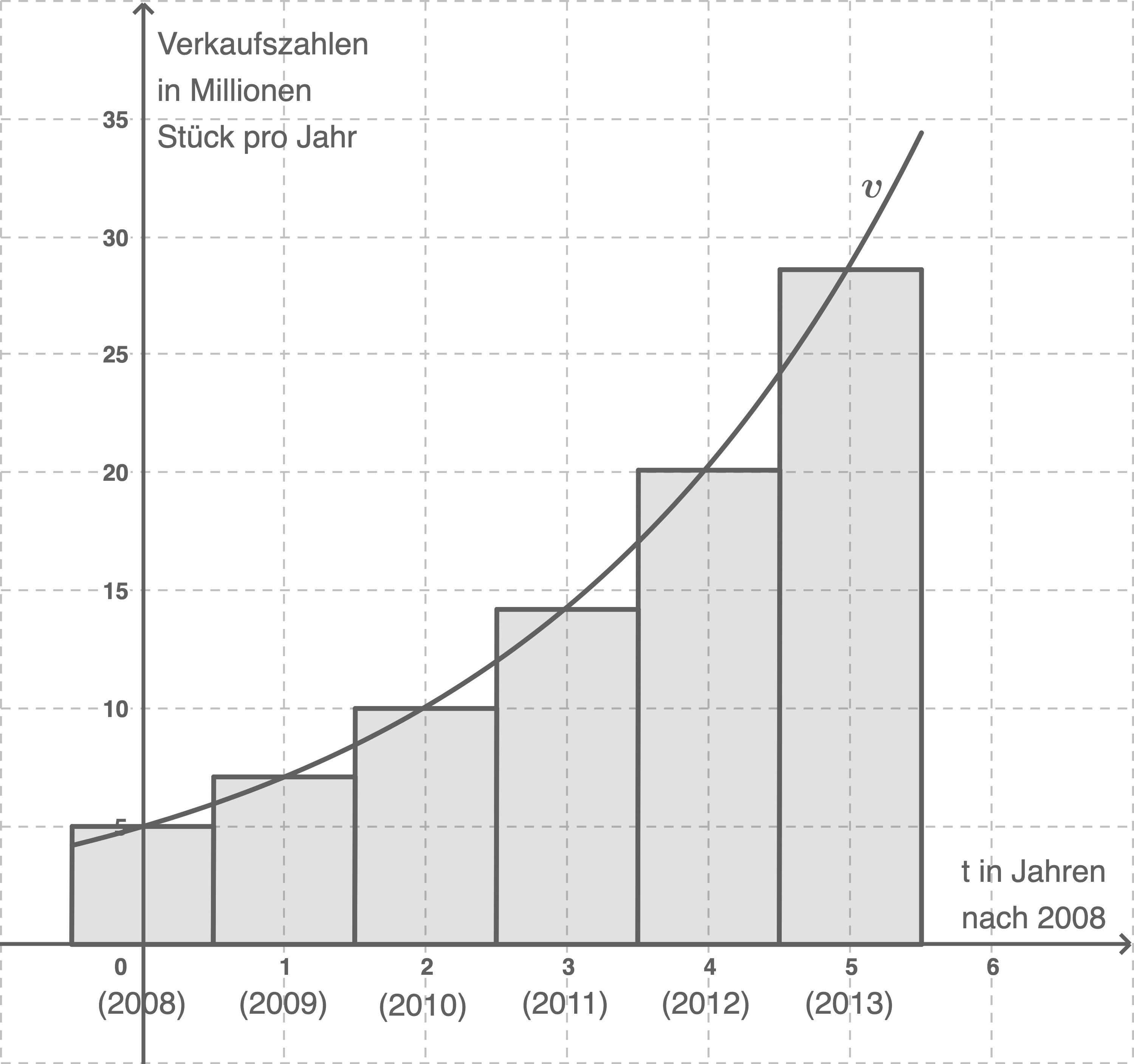
Verkaufszahlen Smartphone Exponentialfunktion Hessen Abi 2016

3.2

$\begin{array}[t]{rll} \displaystyle\int_{0}^{5}f(t)\;\mathrm dt&=&\displaystyle\int_{0}^{5}\; 5 \cdot \mathrm e^{0,351 \cdot t}\;\mathrm dt \\[5pt] &=&5 \cdot \displaystyle\int_{0}^{5} \mathrm e^{0,351\cdot t}\;\mathrm dt \\[5pt] &=& 5 \cdot \displaystyle\int_{0}^{5} \mathrm e^{\frac{351}{1000} \cdot t}\;\mathrm dt \\[5pt] &=&5\cdot \left[\frac{1000}{351} \cdot \mathrm e^{\frac{351}{1000} \cdot t}\right]_0^5 \\[5pt] &=&5 \cdot \frac{1000}{351}\cdot \left[\mathrm e^{\frac{351}{1000}\cdot t}\right]_0^5 \\[5pt] &=&\frac{5000}{351}\cdot \left[\mathrm e^{\frac{351}{1000}\cdot t}\right]_0^5 \\[5pt] &=&\frac{5000}{351}\cdot \left(\mathrm e^{\frac{351}{1000}\cdot 5} - \mathrm e^{\frac{351}{1000}\cdot 0}\right) \\[5pt] &\approx& 68,14\,\text{[Mio.]} \end{array}$

Im Zeitraum von Mitte 2008 bis Mitte 2013 wurden insgesamt 68,14 Millionen Smartphones verkauft.

3.3

Aufsummieren der jeweiligen Verkaufzahlen ergibt:

$5 + 7,1 + 10 + 14,2 + 20,1 + 28,6=85$

Bei der Berechnung mit dem Integral wurde von Null bis 5 integriert, was der Mitte des jeweiligen Jahres entspricht. Hierbei werden die erste Hälfte des Jahres 2008 und die letzte Hälfte des Jahres 2013 nicht miteingerechnet und fehlen somit im berechneten Endwert.

Um das Ergebnis zu verbessern, welches mittels des Integrals berechnet wird, können die Integralgrenzen angepasst werden:

$\displaystyle\int_{-0,5}^{5,5}f(t)\;\mathrm dt$

3.4

Für das Jahr 2030 gilt $t=22.$

$f(22)\approx 11287,35$

Im Jahr 2030 werden nach der Funktion $f$ über 11 Miliarden Smartphones verkauft. Diese Zahl übersteigt bei weitem die in der Aufgabenstellung angegebene Bevölkerung des Landes von 80 Millionen Einwohnern. Somit ist der Wert nicht plausibel.