B1 - Analysis

Das in Abbildung 1 im Schrägbild dargestellte Werkstück hat eine rechteckige Grundfläche und dazu senkrecht verlaufende Seitenflächen. Es besteht aus zwei unterschiedlich gefärbten Kunststoffen. Der obere Teil ist grün, der untere grau gefärbt.

In Abbildung 2 ist eine Querschnittsfläche des Werkstücks abgebildet.

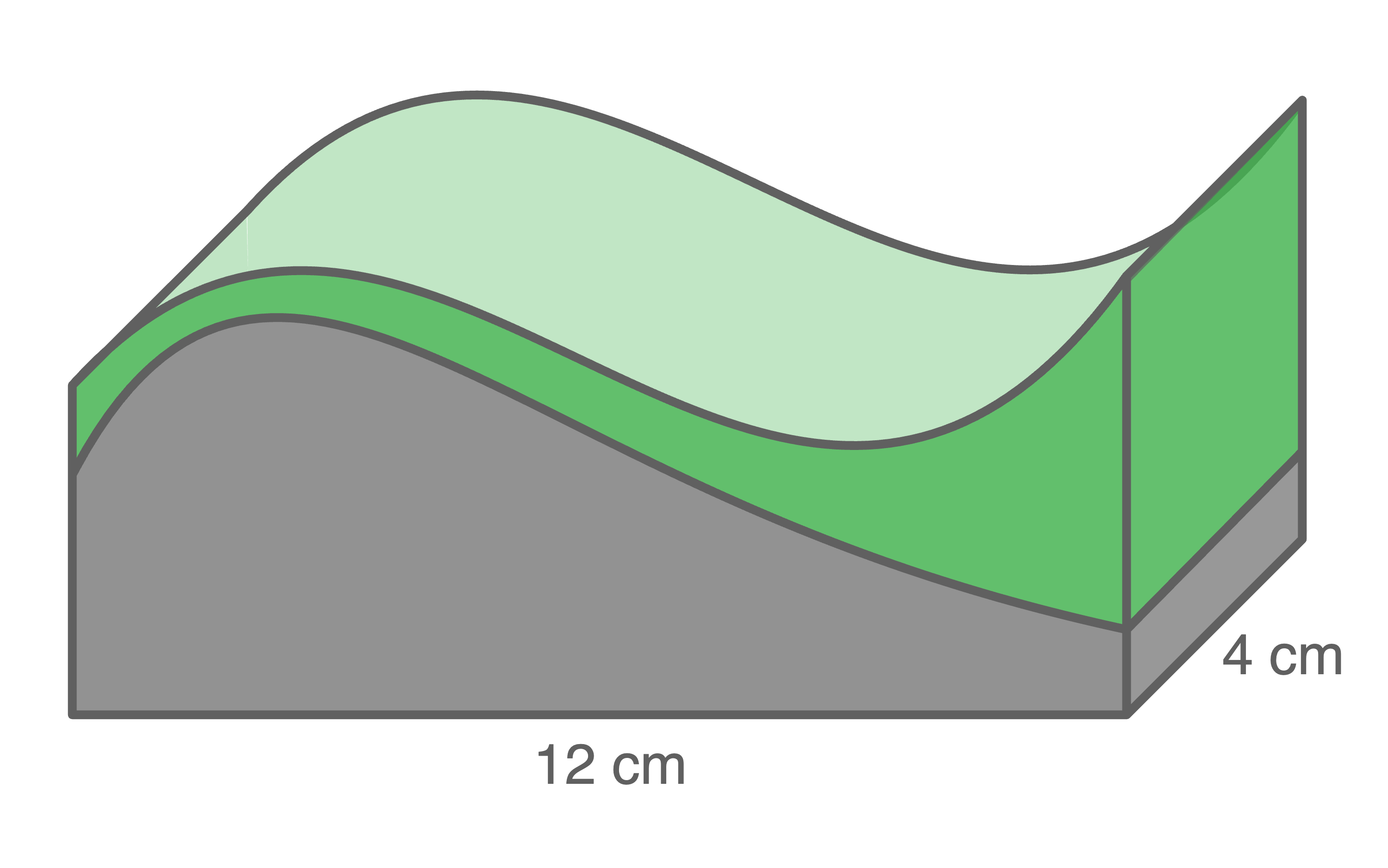
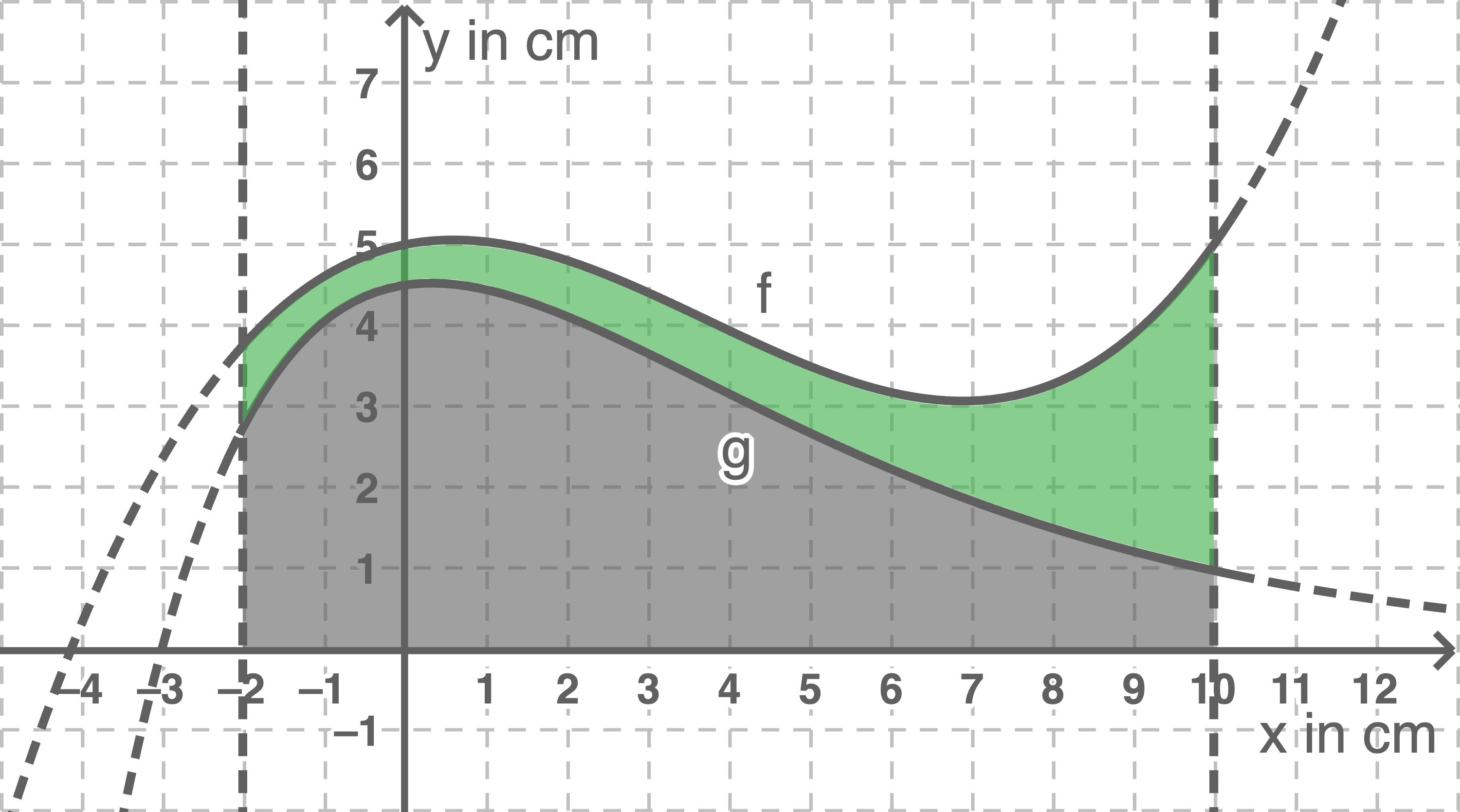
Abbildung 1

Abbildung 2

Die obere Randkurve der Querschnittsfläche kann für $-2\leq x \leq 10$ durch den Graphen der Funktion $f$ mit $f(x)= 0,016x^3-0,18x^2 +0,2x+5$ beschrieben werden (alle Angaben in $\text{cm}$ ).

1.1

Berechne, auch unter Berücksichtigung der Randwerte des Intervalls, an welcher Stelle das Werkstück am höchsten ist, und gib seine maximale Höhe an.

(8 BE)

1.2

Berechne den Inhalt $A$ der gesamten Querschnittsfläche des Werkstücks.

(4 BE)

Die obere Randkurve des unteren, grau gefärbten Teils der Querschnittsfläche kann für $-2\leq x \leq 10$ durch den Graphen der Funktion $g$ mit $g(x)= \left(1,5\cdot x +4,5 \right)\cdot \mathrm e^{-0,3 x}$ beschrieben werden (alle Angaben in $\text{cm}$ ).

2.1

Mit Hilfe des Formansatzes $G(x)=(a\cdot x +b)\cdot \mathrm e^{-0,3x}$ soll eine Stammfunktion $G$ der Funktion $g$ ermittelt werden.

Berechne die Ableitungsfunktion $\(G$ der Funktion $G.$

Ermittle durch Vergleich der Funktionsterme von $\(G$ und $g$ eine Stammfunktion $G$ von $g.$

$\bigg [$ Zur Kontrolle: $G(x)= \left(-5x-\dfrac{95}{3} \right)\cdot \mathrm e^{-0,3x} \bigg ]$

(6 BE)

2.2

Bestimme das Volumen des oberen, grün gefärbten Teils des Werkstücks.

(5 BE)

2.3

Auf der rechten Seite wird ein Teil des Werkstücks durch einen ebenen Schnitt abgetrennt. Die Schnittebene $E$ verläuft dabei senkrecht zur Querschnittsfläche und durch die Punkte $(9\mid 0)$ und $(10\mid 5).$

Erläutere eine Vorgehensweise, mit der man ermitteln kann, um wie viel Kubikzentimeter das in Aufgabe 2.2 bestimmte Volumen des oberen, grün gefärbten Werkstückteils dadurch kleiner wird.

(5 BE)

2.4

Für $x\lt -2$ hat der Graph von $G$ einen relativen Extrempunkt.

Berechne diesen nur anhand der notwendigen Bedingung und begründe unter Verwendung der Abbildung in Abbildung 2, dass es sich um einen relativen Tiefpunkt handeln muss.

(5 BE)

Die Funktion $f$ gehört zu der Funktionenschar $f_k$ mit $f_k(x)=k\cdot x^3-0,18x^2 +0,2x+5$ für $k\gt 0.$

3.1

Berechne die Wendestelle $x_W$ des Graphen von $f_k$ in Abhängigkeit von $k.$

Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.

$\bigg[$ Zur Kontrolle: $\; x_W(k) = \dfrac{3}{50k} \; \bigg]$

(5 BE)

3.2

Untersuche, wie sich die Lage von $x_W(k)$ für $k\to \infty$ ändert.

(2 BE)

1.1

1. Schritt: Ableitungen bestimmen

$\(\begin{array}[t]{rll} f(x) &=& 0,016x^3 - 0,18x^2 + 0,2x + 5 \\[10pt] f$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

Mit der $pq$ -Formel ergibt sich:

$\begin{array}[t]{rll} x_{1/2} &=& -\dfrac{-7,5}{2}\pm \sqrt{\left(\dfrac{-7,5}{2} \right)^2 -\dfrac{25}{6}} \\[5pt] &=& 3,75 \pm \sqrt{(-3,75)^2 -\dfrac{25}{6}} \\[5pt] x_1 &\approx& 0,604 \\[5pt] x_2 &\approx& 6,896 \end{array}$

3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

An der Stelle $x_1 \approx 0,604$ besitzt $f$ somit ein lokales Maximum.

4. Schritt: Maximale Höhe angeben

$f(0,604) \approx 5,059$

Rechenweg anzeigen

Randpunkte untersuchen:

$f(-2)=3,752$

Rechenweg anzeigen

$f(10)=5$

Rechenweg anzeigen

Damit liegt die maximale Höhe des Werkstücks an der Stelle $x\approx 0,604$ und beträgt ca. $5,059\,\text{cm}.$

1.2

Gesucht ist der Inhalt der Fläche unter dem Graphen von $f$ im Bereich $-2\leq x\leq 10.$

Hierfür gilt:

$A= 49,056$

Rechenweg anzeigen

Der Flächeninhalt der gesamten Querschnittsfläche beträgt somit $49,056\,\text{cm}^2.$

2.1

Ableitungsfunktion $\(\boldsymbol{G$ berechnen

Mit der Produktregel folgt:

Rechenweg anzeigen

$\( G$

Koeffizientenvergleich durchführen

$\(\begin{array}[t]{rll} G$

Durch Vergleichen der beiden Funktionsterme ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I:}\quad&1,5 &=& - 0,3a \\ \text{II:}\quad&4,5&=& a - 0,3b \\ \end{array}$

Aus $\text{I}$ folgt:

$\begin{array}[t]{rll} 1,5 &=& -0,3a &\quad \scriptsize \mid\; :(-0,3)\\[5pt] -5 &=& a \end{array}$

Einsetzen in die zweite Gleichung liefert:

$\begin{array}[t]{rll} 4,5 &=& a-0,3b &\quad \scriptsize \mid\;a=-5 \\[5pt] 4,5 &=& -5-0,3b &\quad \scriptsize \mid\;+5 \\[5pt] 9,5 &=& -0,3b &\quad \scriptsize \mid\; :(-0,3) \\[5pt] - \dfrac{95}{3} &=& b \\[5pt] \end{array}$

Eine Stammfunktion von $g$ ist somit $G$ mit $G(x)= \left(-5\cdot x -\dfrac{95}{3} \right)\cdot \mathrm e^{-0,3x}.$

2.2

Das gesuchte Volumen ergibt sich aus dem Flächeninhalt der Grundfläche $G$ und der Tiefe $t = 4\,\text{cm}$ des Werkstücks:

$V= G\cdot t$

Die Grundfläche entspricht der Fläche, die die Graphen von $f$ und $g$ im Bereich $-2\leq x \leq 10$ einschließen:

$G=\displaystyle\int_{-2}^{10}f(x)\;\mathrm dx-\displaystyle\int_{-2}^{10}g(x)\;\mathrm dx$

Es gilt:

$\displaystyle\int_{-2}^{10}g(x)\;\mathrm dx \approx 35,413\,\big[\text{cm}^2 \big]$

Rechenweg anzeigen

Mit dem Ergebnis aus Aufgabe 1.2 folgt nun:

$\begin{array}[t]{rll} G&\approx& 49,056 - 35,413 \\[5pt] &=& 13,643\,\big[\text{cm}^2 \big] \end{array}$

Somit ergibt sich:

$\begin{array}[t]{rll} V &=& G\cdot t \\[5pt] &\approx& 13,643\,\text{cm}^2 \cdot 4\,\text{cm} \\[5pt] &=& 54,572\,\text{cm}^3 \end{array}$

Der obere, grün gefärbte Teil des Werkstücks besitzt also ein Volumen von ca. $54,572\,\text{cm}^3.$

2.3

Durch den Schnitt wird der obere, grüne Teil des Werkstücks in zwei Teilkörper geteilt. Von der Querschnittsfläche mit dem Inhalt $G$ wird dabei entlang einer Geraden $h$ eine Fläche mit dem Flächeninhalt $A_Δ$ abgetrennt.

Da die Schnittebene senkrecht zur Querschnittsfläche verläuft, können die Volumina der beiden Teilkörper wie in Aufgabe 2.2 berechnet werden.

Für das Volumen des abgetrennten Teils des Werkstücks gilt also:

$V_Δ = A_Δ \cdot t = A_Δ \cdot 4\,\text{cm}$

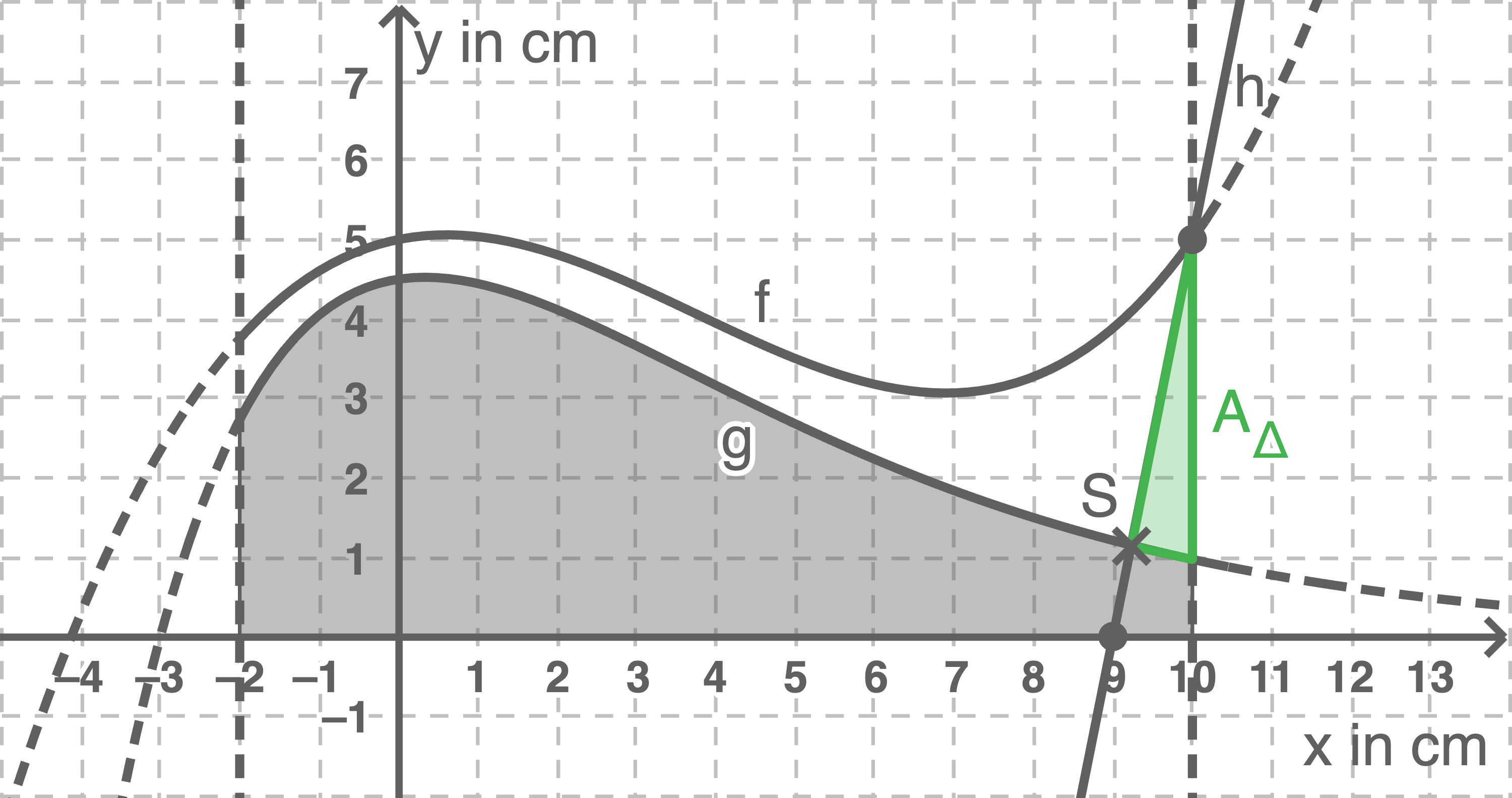
Hilfsskizze

Der Flächeninhalt $A_Δ$ kann nun wie folgt berechnet werden:

Aufstellen einer Gleichung der Geraden $h,$ die durch die beiden Punkte $(9\mid 0)$ und $(10\mid 5)$ verläuft.
Bestimmen der Schnittstelle $x_S$ von $h$ und $g.$
Flächeninhalt berechnen:
$A_ Δ = \displaystyle\int_{x_S}^{10}(h(x)-g(x))\;\mathrm dx$
Volumen des abgeschnittenen Teils berechnen: $V_2 = A_2 \cdot 4\,\text{cm}$

2.4

Relativen Extrempunkt berechnen

Notwendige Bedingung für Extremstellen anwenden:

$\( G$

Rechnung anzeigen

Da die Untersuchung der notwendigen Bedingung laut Aufgabenstellung genügt, folgt, dass der relative Extrempunkt des Graphen von $G$ für $x\lt -2$ die $x$ -Koordinate $x=-3$ besitzt.

$y$ -Koordinate berechnen:

$\begin{array}[t]{rll} G(-3) &=& \left(-5\cdot (-3) -\dfrac{95}{3}\right)\cdot \mathrm e^{-0,3\cdot (-3)} \\[5pt] &=& -\dfrac{50}{3}\cdot \mathrm e^{0,9} \\[5pt] &\approx& -40,99\\[5pt] \end{array}$

Der relative Extrempunkt des Graphen von $G$ für $x \lt -2$ besitzt somit die Koordinaten $E\left(-3\mid -\dfrac{50}{3}\cdot \mathrm e^{0,9}\right).$

Begründung

Da $g$ die erste Ableitungsfunktion von $G$ ist, beschreibt der Graph von $g$ die Steigung des Graphen von $G.$

Abbildung 2 kann entnommen werden, dass $g$ an der Stelle $x=-3$ eine Nullstelle besitzt. An dieser Nullstelle wechselt $g$ das Vorzeichen von negativ zu positiv. Der Graph von $G$ besitzt daher zunächst eine negative Steigung und geht dann an der Stelle $x=-3$ in eine positive Steigung über.

Somit sind alle Kriterien für die Existenz eines relativen Tiefpunkts erfüllt.

3.1

1. Schritt: Ableitungsfunktionen bestimmen