B1 - Analytische Geometrie
Anlässlich der documenta 6 wurde 1977 in Kassel ein Laserkunstwerk errichtet, das historisch markante Punkte der Stadt durch deutlich sichtbare geradlinig verlaufende Laserstrahlen verbindet.
In einer anderen Stadt soll ein ähnliches Kunstwerk installiert werden. Die drei geplanten Laserstrahlen verbinden wichtige Punkte der Stadt (Angaben in Metern):
1
Ermittle, ob die Punkte  und
und  in einer Ebene liegen.
in einer Ebene liegen.
(6 BE)
2
Zur Finanzierung des Kunstwerks soll wie damals in Kassel die Länge des längsten Laserstrahles in einzelnen Meterabschnitten für jeweils  an Kunstfreunde „verkauft“ werden.
an Kunstfreunde „verkauft“ werden.
2.1
Berechne die Einnahmen unter der Annahme, dass für alle vollen Meterabschnitte des längsten Strahles Käufer gefunden werden.
(4 BE)
2.2
Zeichne die Laserstrahlen in einen Grundriss der Stadt im Maßstab  ein.
Hierbei liegt die Grundfläche der Stadt in der
ein.
Hierbei liegt die Grundfläche der Stadt in der  -Ebene und die
-Ebene und die  -Achse zeigt senkrecht zur
-Achse zeigt senkrecht zur  -Ebene in Richtung des Betrachters.
Begründe, warum nicht allein anhand des Grundrisses der längste Strahl ermittelt werden kann.
-Ebene in Richtung des Betrachters.
Begründe, warum nicht allein anhand des Grundrisses der längste Strahl ermittelt werden kann.
(5 BE)
3
Die blaue Laserlichtquelle im Funkturm kann stufenlos so gedreht werden, dass sie nicht mehr zum Bahnhof, sondern zum Schloss leuchtet. Schwenkt man die Lichtquelle sehr schnell, nimmt der Beobachter diese Strahlen als Teil einer Ebene wahr.
3.1
Bestimme die Gleichung dieser Ebene in Parameter- und Koordinatenform.
(7 BE)
3.2
Berechne den Winkel, um den die blauen Laserstrahlen im Funkturm schwenken.
(3 BE)
3.3
Im Punkt  steht ein 50 Meter hoher Kirchturm. Ein künstlerischer Berater des Projekts befürchtet, dass der Kirchturm beim Schwenken die blauen Laserstrahlen unterbricht und die Wirkung des Kunstwerks stört.
Untersuche, ob der Kirchturm im Schwenkbereich der Laserstrahlen steht.
steht ein 50 Meter hoher Kirchturm. Ein künstlerischer Berater des Projekts befürchtet, dass der Kirchturm beim Schwenken die blauen Laserstrahlen unterbricht und die Wirkung des Kunstwerks stört.
Untersuche, ob der Kirchturm im Schwenkbereich der Laserstrahlen steht.
(5 BE)
1
1. Schritt: Parametergleichung aufstellen
Eine Parametergleichung einer Ebene, in der drei der vier gegebenen Punkte liegen, ist beispielsweise:
2. Schritt: Punktprobe durchführen
Der Punkt  liegt genau dann in der gleichen Ebene wie
liegt genau dann in der gleichen Ebene wie  und
und  wenn gilt:
Aus der Gleichung lässt sich folgendes lineare Gleichungssystem aufstellen:
wenn gilt:
Aus der Gleichung lässt sich folgendes lineare Gleichungssystem aufstellen:
 Aus
Aus  folgt:
folgt:
![\(\begin{array}[t]{rll}
800&=& s\cdot 200 +t\cdot 1400&\quad \scriptsize \mid\; :200 \\[5pt]
4&=& s+7t&\quad \scriptsize \mid\; -7t \\[5pt]
4-7t&=& s
\end{array}\)](https://www.schullv.de/resources/formulas/701f504521aa75c5621a86a6cf6b1787ed9ea4ec8fedf13048c0fb6e6ffd43df_light.svg) Einsetzen in
Einsetzen in  liefert:
liefert:
![\(\begin{array}[t]{rll}
400&=& s\cdot 500+t\cdot 1200&\quad \scriptsize \mid\; :100 \\[5pt]
4&=& 5s+12t&\quad \scriptsize \mid\; s=4-7t\\[5pt]
4&=& 5\cdot (4-7t)+12t & \\[5pt]
4&=& 20-35t+12t &\quad \scriptsize \mid\;- 20 \\[5pt]
-16&=& -23t &\quad \scriptsize \mid\;: (-23)\\[5pt]
\dfrac{16}{23}&=& t
\end{array}\)](https://www.schullv.de/resources/formulas/86f7f260218c92845fe8362287aa356fa55595b785cf828638e2e38e471b9f16_light.svg) Somit folgt
Somit folgt  Überprüfen durch Einsetzen in
Überprüfen durch Einsetzen in 
![\(\begin{array}[t]{rll}
130&=& \left(-\dfrac{20}{23}\right) \cdot 30 + \dfrac{16}{23}\cdot 230 & \\[5pt]
130&\approx& 133,91
\end{array}\)](https://www.schullv.de/resources/formulas/1e8a00b4f67504c3e0e6f35bf2de616fd04c05d821be8e7bfd4222b85c85aa10_light.svg) Somit besitzt das Gleichungssystem keine Lösung und der Punkt
Somit besitzt das Gleichungssystem keine Lösung und der Punkt  liegt folglich nicht in einer Ebene mit den Punkten
liegt folglich nicht in einer Ebene mit den Punkten  und
und 
2.1
1. Schritt: Längen der Laserstrahlen berechnen
Die Laserstrahlen entsprechen den Verbindungsvektoren der jeweiligen Punkte in der Tabelle aus der Aufgabenstellung:
![\(\begin{array}[t]{rll}
\mid \overrightarrow{r} \mid &=& \mid \overrightarrow{MB} \mid & \\[5pt]
&=& \left| \begin{pmatrix}200\\500\\30\end{pmatrix} \right| & \\[5pt]
&=& \sqrt{200^2 + 500^2 + 30^2}& \\[5pt]
&\approx& 539,35
\end{array}\)](https://www.schullv.de/resources/formulas/d786acdb2a4cef0f7608d51923e68789dee71c27dc7d186329b65948c4f643a1_light.svg) 2. Schritt: Einnahmen berechnen
Der längste Laserstrahl ist der blaue mit 1403 vollen Metern.
Damit ergibt sich:
2. Schritt: Einnahmen berechnen
Der längste Laserstrahl ist der blaue mit 1403 vollen Metern.
Damit ergibt sich:
![\(E = 1403\cdot 10 = 14030 \;[\,€]\)](https://www.schullv.de/resources/formulas/f0461df95a7ca4d80a80d2b6c16f01067e827fdbe9f3da0ae9eb55b2801a66d7_light.svg) Die Einnahmen betragen somit
Die Einnahmen betragen somit 
2.2
Der Maßstab des Grundrisses ist vorgegeben mit  Es gilt also:
Es gilt also:
 Im folgenden Koordinatensystem entspricht eine Kästchenlänge
Im folgenden Koordinatensystem entspricht eine Kästchenlänge 
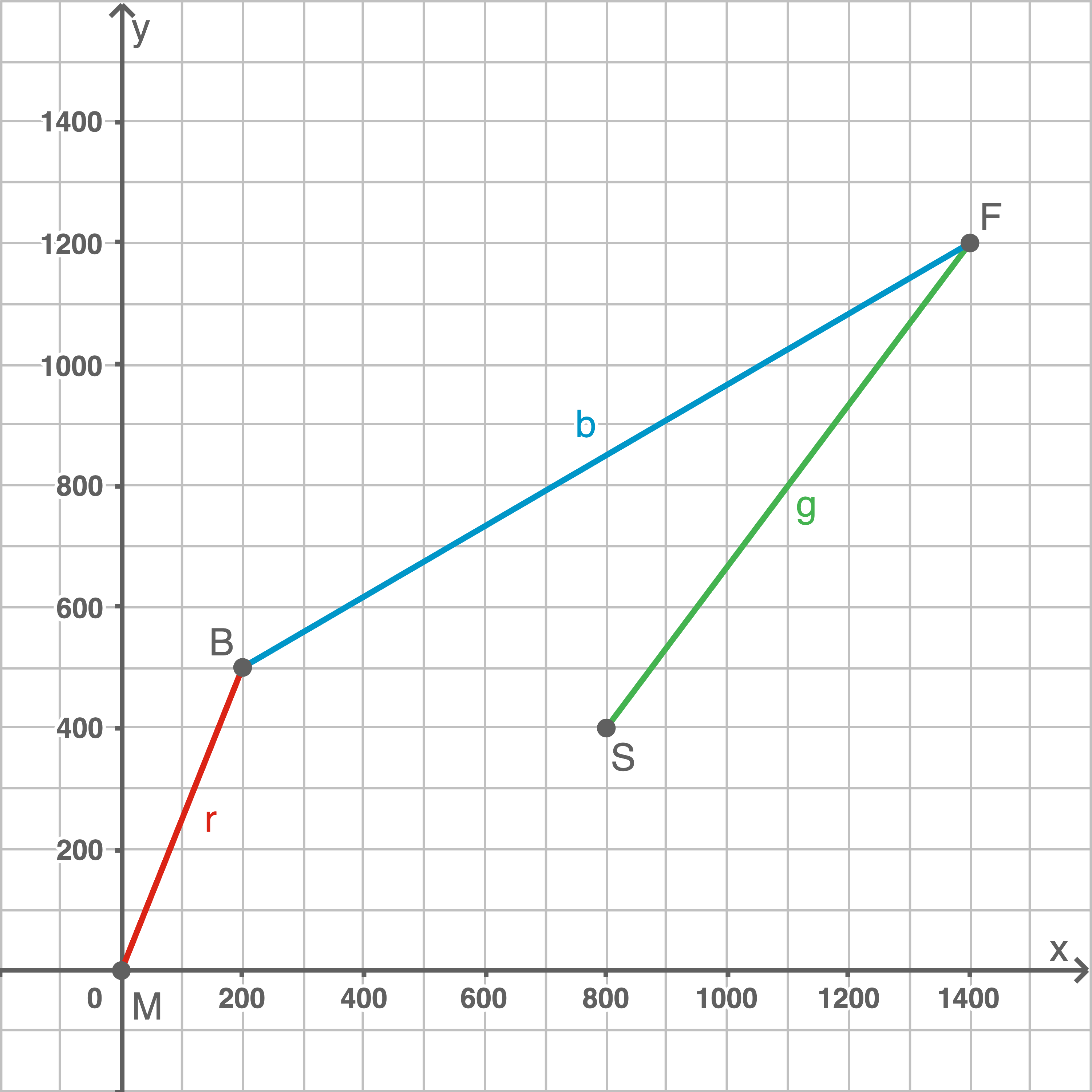 Begründung
Im vorherigen Aufgabenteil wurde bereits die Länge der Vektoren berechnet. Diese wird anhand der
Begründung
Im vorherigen Aufgabenteil wurde bereits die Länge der Vektoren berechnet. Diese wird anhand der  und
und  Koordinaten berechnet und bezieht sich somit auf alle drei Dimensionen.
Der Grundriss der Stadt hingegen stellt nur die
Koordinaten berechnet und bezieht sich somit auf alle drei Dimensionen.
Der Grundriss der Stadt hingegen stellt nur die  -Ebene dar und vernachlässigt die Höhendifferenz der Laserstrahlen. Ein Strahl, der senkrecht vom Boden nach oben zeigt, hätte demnach beispielsweise die Länge Null, obwohl er in Wahrheit viel länger ist.
Für die genaue Länge muss somit auch die
-Ebene dar und vernachlässigt die Höhendifferenz der Laserstrahlen. Ein Strahl, der senkrecht vom Boden nach oben zeigt, hätte demnach beispielsweise die Länge Null, obwohl er in Wahrheit viel länger ist.
Für die genaue Länge muss somit auch die  -Koordinate der Vektoren betrachtet werden.
-Koordinate der Vektoren betrachtet werden.

3.1
Parameterform aufstellen
Koordinatenform bestimmen
Ein Normalenvektor der Ebene ergibt sich aus dem Kreuzprodukt der Richtungsvektoren:
Einsetzen des gekürzten Normalenvektors in die allgemeine Koordinatengleichung liefert:
![\(\begin{array}[t]{rll}
E: n_1\cdot x+n_2\cdot y+n_3\cdot z&=& d&\\[5pt]
-x+6z&=& d
\end{array}\)](https://www.schullv.de/resources/formulas/c80a503cffdab68f2f5dd8f77935d036b7245afbdc2222ba1e1f8209915d5278_light.svg) Punktprobe mit
Punktprobe mit  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
-1400+6\cdot 230&=& d & \\[5pt]
-20&=& d
\end{array}\)](https://www.schullv.de/resources/formulas/0d1161e211575d30bbf39b7a1945da4297cc1a8590099877b82fd685e06cbddb_light.svg) Damit lautet die Gleichung der Ebene:
Damit lautet die Gleichung der Ebene:

3.2
Der Winkel, um den die blauen Laserstrahlen im Funkturm schwenken, entspricht dem Schnittwinkel der beiden Verbindungsvektoren  und
und  Mit der allgemeinen Formel für den Schnittwinkel zwischen zwei Vektoren foglt:
Die blauen Lichtstrahlen schwenken folglich in einem Winkel von ca.
Mit der allgemeinen Formel für den Schnittwinkel zwischen zwei Vektoren foglt:
Die blauen Lichtstrahlen schwenken folglich in einem Winkel von ca.  um den Funkturm.
um den Funkturm.
3.3
Um herauszufinden, ob der Kirchturm in der Ebene liegt, die durch die blauen Laserstrahlen aufgespannt wird, wird eine Gleichung der Geraden aufgestellt, in der der Kirchturm liegt, und der Schnittpunkt mit der Ebene berechnet.
Mit dem Punkt  ergibt sich für den senkrecht stehenden Kirchturm:
ergibt sich für den senkrecht stehenden Kirchturm:
![\(\begin{array}[t]{rll}
g: \overrightarrow{x}&=& \overrightarrow{OK}+t\cdot \pmatrix{0\\0\\1} & \\[5pt]
&=& \pmatrix{900\\700\\90} +t\cdot \pmatrix{0\\0\\1} & \\[5pt]
&=& \pmatrix{900\\700\\90+t}
\end{array}\)](https://www.schullv.de/resources/formulas/497471c40a35f30a49c946a0f768c6f1b6894e588798c19d8645e980f9a22468_light.svg) Einsetzen des allgemeinen Koordinatenpunkts von
Einsetzen des allgemeinen Koordinatenpunkts von  in die Ebenengleichung
in die Ebenengleichung  liefert:
liefert:
![\(\begin{array}[t]{rll}
-x+6z&=& -20 & \\[5pt]
-900+6\cdot (90+t)&=& -20 & \\[5pt]
-900+540+6t&=& -20 & \\[5pt]
-360+6t&=& -20 &\quad \scriptsize \mid\; +360 \\[5pt]
6t&=& 340 &\quad \scriptsize \mid\;:(-6) \\[5pt]
t&\approx& 56,67
\end{array}\)](https://www.schullv.de/resources/formulas/b3b70f1d27223591f2b76cb6cc4e3f1cbad25394c83d54306c7215e87c8194f6_light.svg) Durch Einsetzen von
Durch Einsetzen von  in
in  folgt nun:
folgt nun:
 Der Punkt, in dem sich die Gerade, in der der Kirchturm liegt, und die Ebene, in der die Laserstrahlen geschwenkt werden, schneiden, ist somit gegeben durch
Der Punkt, in dem sich die Gerade, in der der Kirchturm liegt, und die Ebene, in der die Laserstrahlen geschwenkt werden, schneiden, ist somit gegeben durch  Da der Kirchturm insgesamt nur
Da der Kirchturm insgesamt nur  hoch ist und somit unterhalb der Ebene endet und diese nicht schneidet, steht der Kirchturm folglich nicht im Schwenkbereich der Laserstrahlen.
hoch ist und somit unterhalb der Ebene endet und diese nicht schneidet, steht der Kirchturm folglich nicht im Schwenkbereich der Laserstrahlen.