A2 - Analysis
Gegeben ist die Funktion  mit
mit  . In den nachfolgenden beiden Abbildungen ist der Graph dieser Funktion dargestellt.
. In den nachfolgenden beiden Abbildungen ist der Graph dieser Funktion dargestellt.
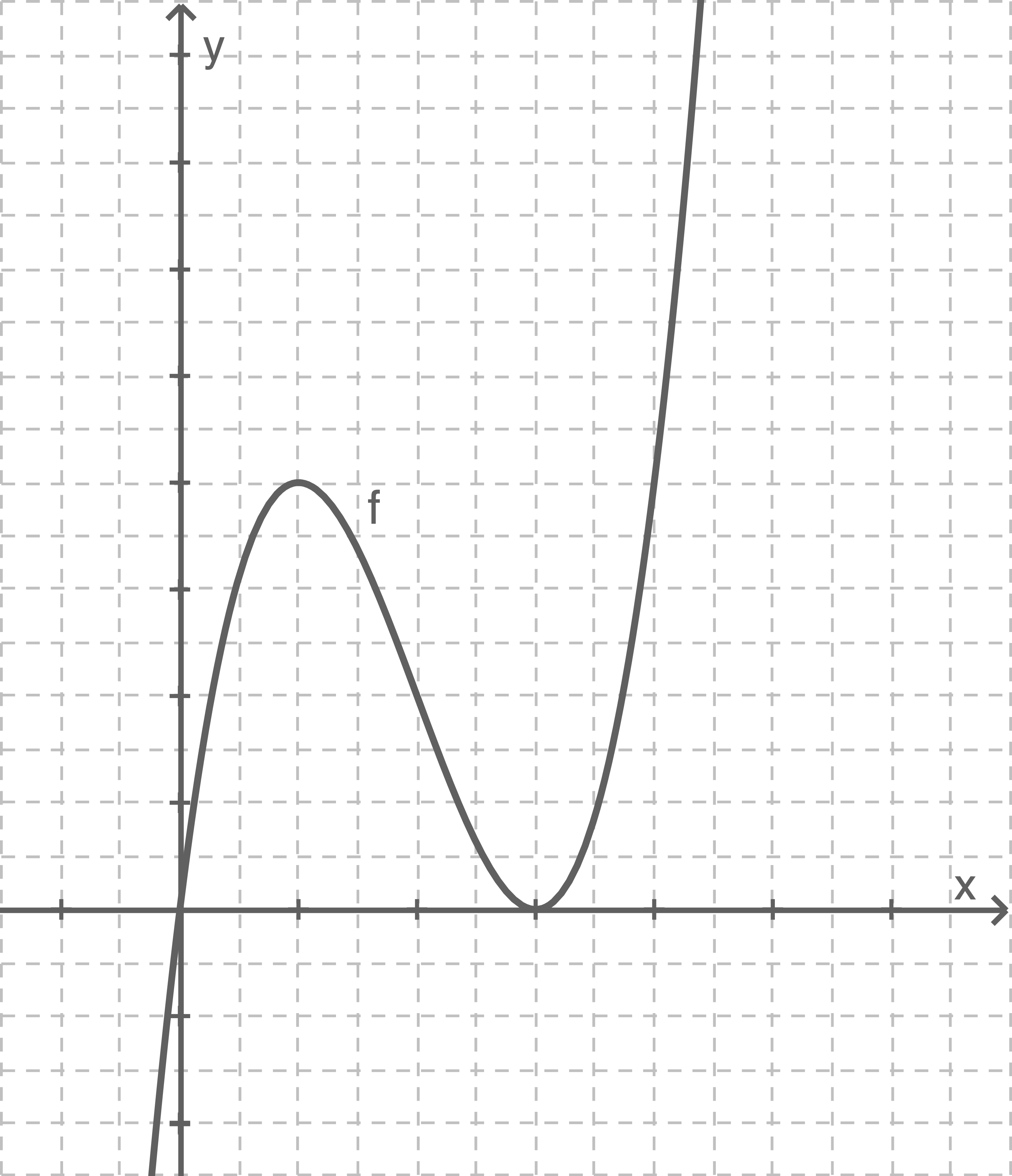


Abbildung 1

Abbildung 2
1.
1.1
Berechne ohne Bezugnahme auf den Graphen die Koordinaten der Extrempunkte sowie des Wendepunktes  des Graphen von
des Graphen von  und gib in Abbildung 1 die Skalierung der Achsen des Koordinatensystems an.
und gib in Abbildung 1 die Skalierung der Achsen des Koordinatensystems an.
(7 BE)
1.2
Ermittle die Gleichung der Geraden  , die durch den Hochpunkt
, die durch den Hochpunkt  und den Tiefpunkt
und den Tiefpunkt  des Graphen verläuft, und zeige, dass der Wendepunkt
des Graphen verläuft, und zeige, dass der Wendepunkt  ebenfalls auf der Geraden
ebenfalls auf der Geraden  liegt.
liegt.
(4 BE)
2.
Skizziere den Graphen einer möglichen Stammfunktion  der Funktion
der Funktion  in das Koordinatensystem von Abbildung 1. Begründe den Verlauf des Graphen von
in das Koordinatensystem von Abbildung 1. Begründe den Verlauf des Graphen von  mithilfe des Verlaufs des Graphen von
mithilfe des Verlaufs des Graphen von  durch Benutzen des Zusammenhangs zwischen Funktionen und ihren Ableitungen.
durch Benutzen des Zusammenhangs zwischen Funktionen und ihren Ableitungen.
(9 BE)
3.
Gegeben ist für  die Funktionenschar
die Funktionenschar  mit
mit  ,
, 
3.1
Erläutere, dass  eine Schar linearer Funktion ist, und zeichne den Graphen von
eine Schar linearer Funktion ist, und zeichne den Graphen von  für
für  in das Koordinatensystem in Abbildung 2.
in das Koordinatensystem in Abbildung 2.
 zur Kontrolle:
zur Kontrolle: ![\(h_a(x)=\ (a^2-6a+9) \cdot x]\)](https://www.schullv.de/resources/formulas/af6aaf2a0dd3189a5b062d8c672664d0c404ffdf31b9b4e0d6b6c2f57abe8926_light.svg)
(5 BE)
3.2
Berechne den Inhalt der endlichen Fläche, die von dem Graphen von  und dem Graphen von
und dem Graphen von  eingeschlossen wird.
eingeschlossen wird.
(7 BE)
4.
Es sei  mit
mit  ein Punkt des Graphen von
ein Punkt des Graphen von  und
und  der Koordinatenursprung. Die Parallele zur
der Koordinatenursprung. Die Parallele zur  -Achse durch
-Achse durch  schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt  .
Zeige, dass der Term
.
Zeige, dass der Term  den Flächeninhalt des Dreiecks
den Flächeninhalt des Dreiecks  beschreibt.
Bestimme
beschreibt.
Bestimme  so, dass
so, dass  extremal wird. Ermittle in allen Extremfällen den Flächeninhalt des Dreiecks und beschreibe jeweils die zugehörige Form des Dreiecks.
extremal wird. Ermittle in allen Extremfällen den Flächeninhalt des Dreiecks und beschreibe jeweils die zugehörige Form des Dreiecks.
(8 BE)
1.
1.1
Koordinaten der Extrempunkte berechnen
1. Schritt: Ableitungen bestimmen
![\(\begin{array}[t]{rll}
f(x)&=& x^3-6x^2+9x &\quad \scriptsize \\[5pt]
f](https://www.schullv.de/resources/formulas/a57d6313a88ce23d1fdf180bd495a5d9a8d39c08bab447c2395f6ca993ff4ab6_light.svg) 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/017aba214984374e264a3d3ec3a9bc91357f4b24d8beb7386dcba8a7148c0067_light.svg) Mit der pq-Formel folgt:
Mit der pq-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1,2} &=& -\dfrac{-4}{2}\pm\sqrt{ \left(\dfrac{-4}{2} \right)^2-3} \\[5pt]
x_{1,2} &=& 2\pm\sqrt{4-3} \\[5pt]
x_1 &=& 3 \\[5pt]
x_2 &=& 1 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/65e5a1a20a6f01762bab1239fd4605dd22d9430fda0f4af3396fab14c44cf881_light.svg) 3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/ebc2b03def40041e5cbb4e6b861ff1615d333e1bf2db67b56c446ddd3b7bf7b4_light.svg)
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/13fd36ae09d328f1c092d7f1c00dd91940fcda525241962a02e8d1c1158b7fe0_light.svg) 4. Schritt:
4. Schritt:  -Koordinaten berechnen
-Koordinaten berechnen
![\(\begin{array}[t]{rll}
f(3)&=& 3^3-6\cdot 3^2+9 \cdot 3& \\[5pt]
&=&0
\end{array}\)](https://www.schullv.de/resources/formulas/660071cdb26d46657d2498fd13ac16e2bcc44726b86229bb6d3a08358e9f947e_light.svg)
![\(\begin{array}[t]{rll}
f(1)&=& 1^3-6\cdot 1^2+9 \cdot 1& \\[5pt]
&=& 4
\end{array}\)](https://www.schullv.de/resources/formulas/f06ec98101f20e1b3538c375e420751b5c55df2005817a0cf8f8721e24f1f4db_light.svg) Die Koordinaten des Hochpunkts folgen somit mit
Die Koordinaten des Hochpunkts folgen somit mit  und die Koordinaten des Tiefpunkts mit
und die Koordinaten des Tiefpunkts mit  Koordinaten des Wendepunkts
Koordinaten des Wendepunkts  berechnen
1. Schritt: Notwendige Bedingung für Wendestellen anwenden
berechnen
1. Schritt: Notwendige Bedingung für Wendestellen anwenden
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/18cee9ebc596d9a4023a088d26fe71edc28a8b74ed2b784a9ad27513465250c3_light.svg) 2. Schritt: Hinreichende Bedingung für Wendestellen anwenden
2. Schritt: Hinreichende Bedingung für Wendestellen anwenden
 An der Stelle
An der Stelle  besitzt der Graph der Funktion von
besitzt der Graph der Funktion von  somit eine Wendestelle.
3. Schritt:
somit eine Wendestelle.
3. Schritt:  -Koordinate bestimmen
-Koordinate bestimmen
![\(\begin{array}[t]{rll}
f(2)&=& 2^3-6 \cdot 2^2+9 \cdot 2& \\[5pt]
&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/5bcedbae6a249fa5d2bfc809e78f5bee5a8bc375891ba0e6ac548ef4f7e6ab01_light.svg) Somit besitzt
Somit besitzt  die Extrem- und Wendepunkte
die Extrem- und Wendepunkte  ,
,  und
und  Skalierung der Achsen angeben
Skalierung der Achsen angeben
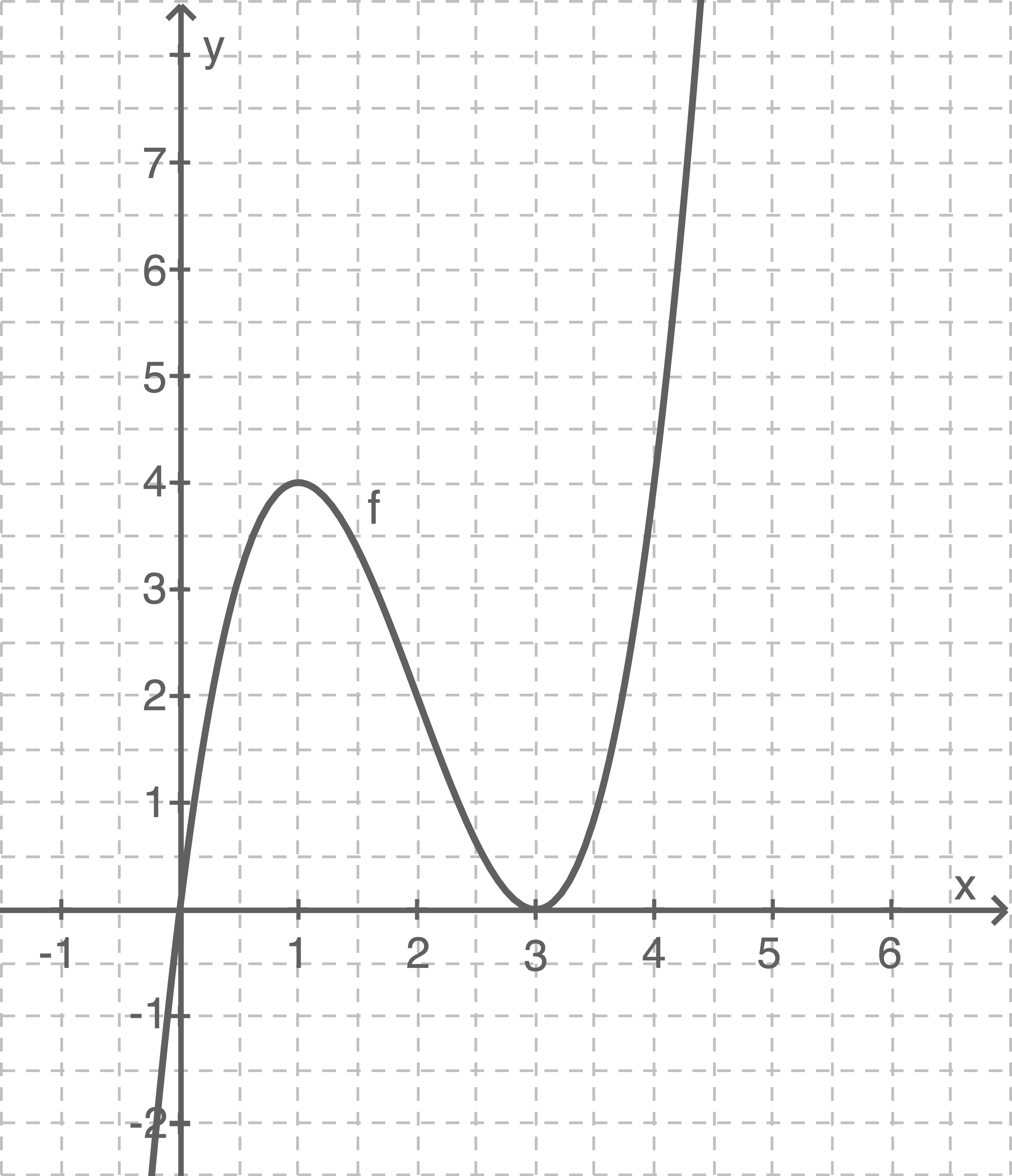

1.2
Es gilt:
 Mit den Koordinaten der Punkte
Mit den Koordinaten der Punkte  und
und  folgt für die Steigung
folgt für die Steigung  der Geraden:
der Geraden:
![\(\begin{array}[t]{rll}
m&=& \dfrac{y_2-y_1}{x_2-x_1} \\[5pt]
&=& \dfrac{0-4}{3-1} \\[5pt]
&=& -\dfrac{4}{2} \\[5pt]
&=& -2
\end{array}\)](https://www.schullv.de/resources/formulas/455a17dbd9d390e312c8f31f5bdfc63e79612790493122382a74f5e73cb74104_light.svg) Einsetzen von
Einsetzen von  und
und  in die allgemeine Geradengleichung
in die allgemeine Geradengleichung  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
0 &=& 3\cdot (-2) + c &\quad \scriptsize \mid\; +6 \\[5pt]
6 &=& c
\end{array}\)](https://www.schullv.de/resources/formulas/f2fda605533ca724d79a76e069848defad8a176ab55fe89de44fb976d0b10d00_light.svg) Somit folgt die Geradengleichung von
Somit folgt die Geradengleichung von  mit:
mit:
 Einsetzen der Koordinaten des Wendepunkts in die Geradengleichung:
Einsetzen der Koordinaten des Wendepunkts in die Geradengleichung:
![\(\begin{array}[t]{rll}
g(2)&=& 2 & \\[5pt]
-2\cdot 2+6 &=& 2 \\[5pt]
2&=& 2 & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/37fe45cd1c535b0163efc0f2b2b416c7e8ffec8cd1bd5436f095bc49584bc602_light.svg) Somit liegt auch der Wendepunkt
Somit liegt auch der Wendepunkt  der Funktion
der Funktion  auf der Geraden
auf der Geraden 
2.
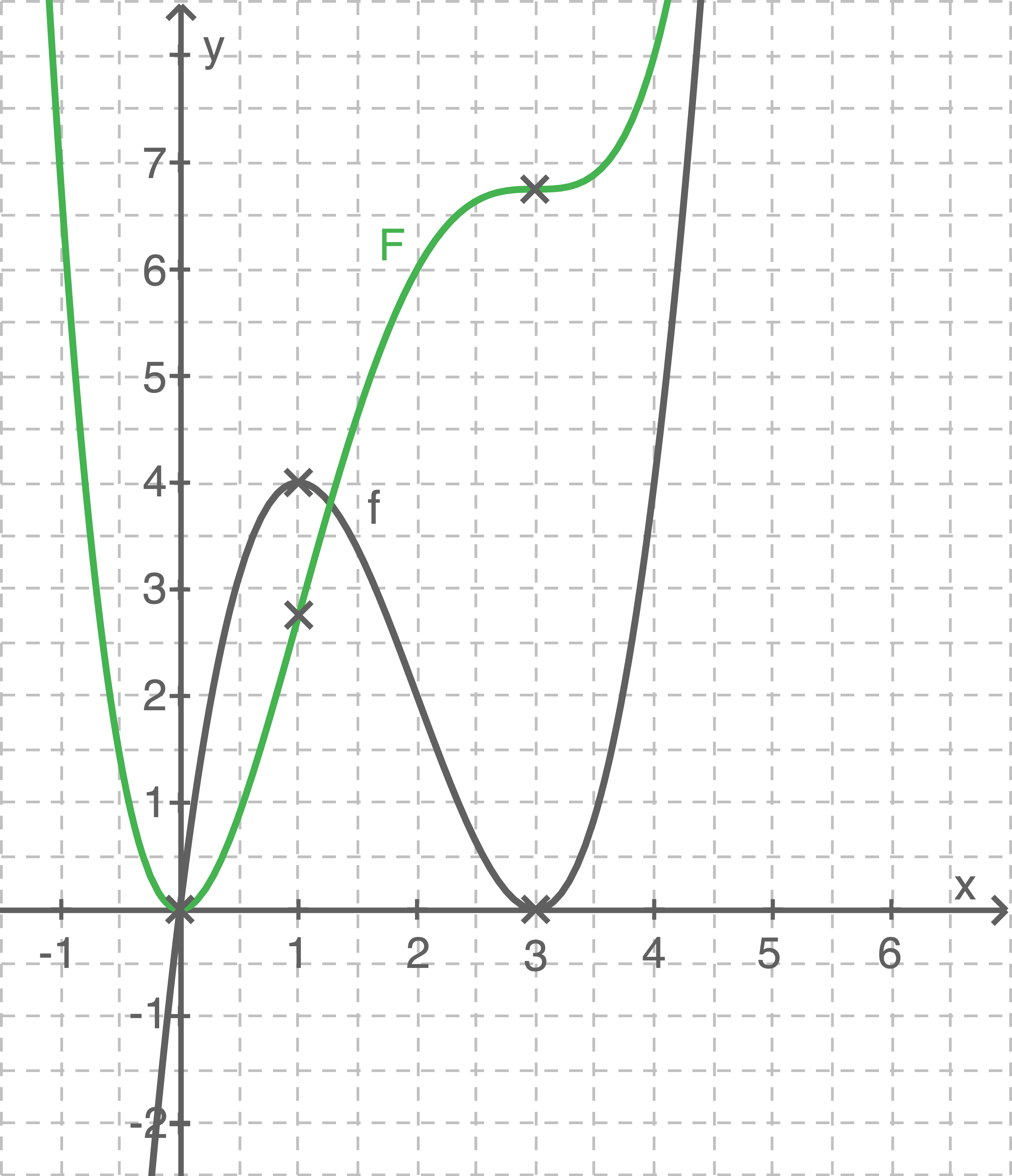
3.
3.1
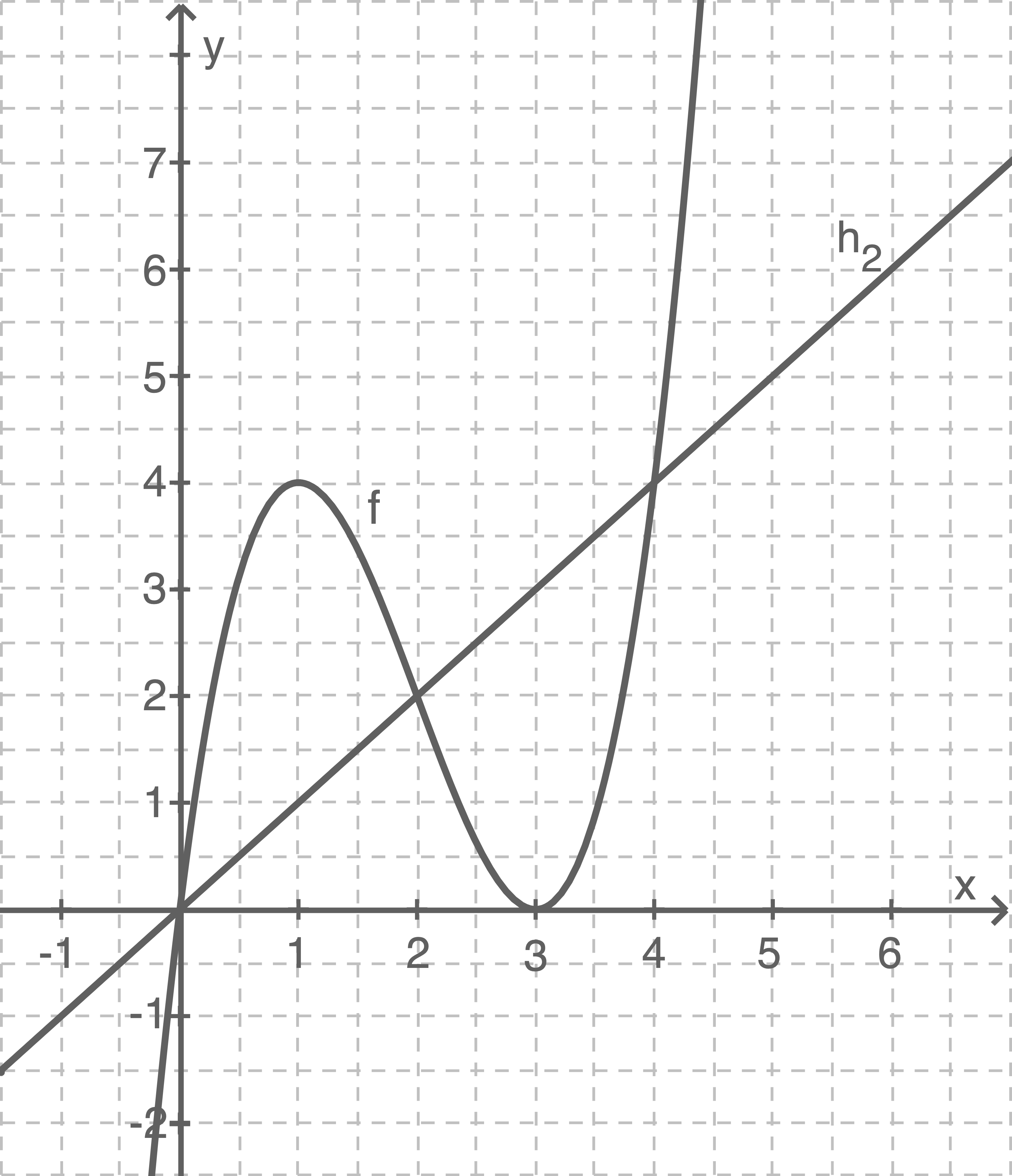
3.2
Aus der Symmetrie des Graphen lässt sich ableiten, dass die eingezeichnete Gerade mit dem Graphen zwei gleichgroße Teilflächen einschließt:
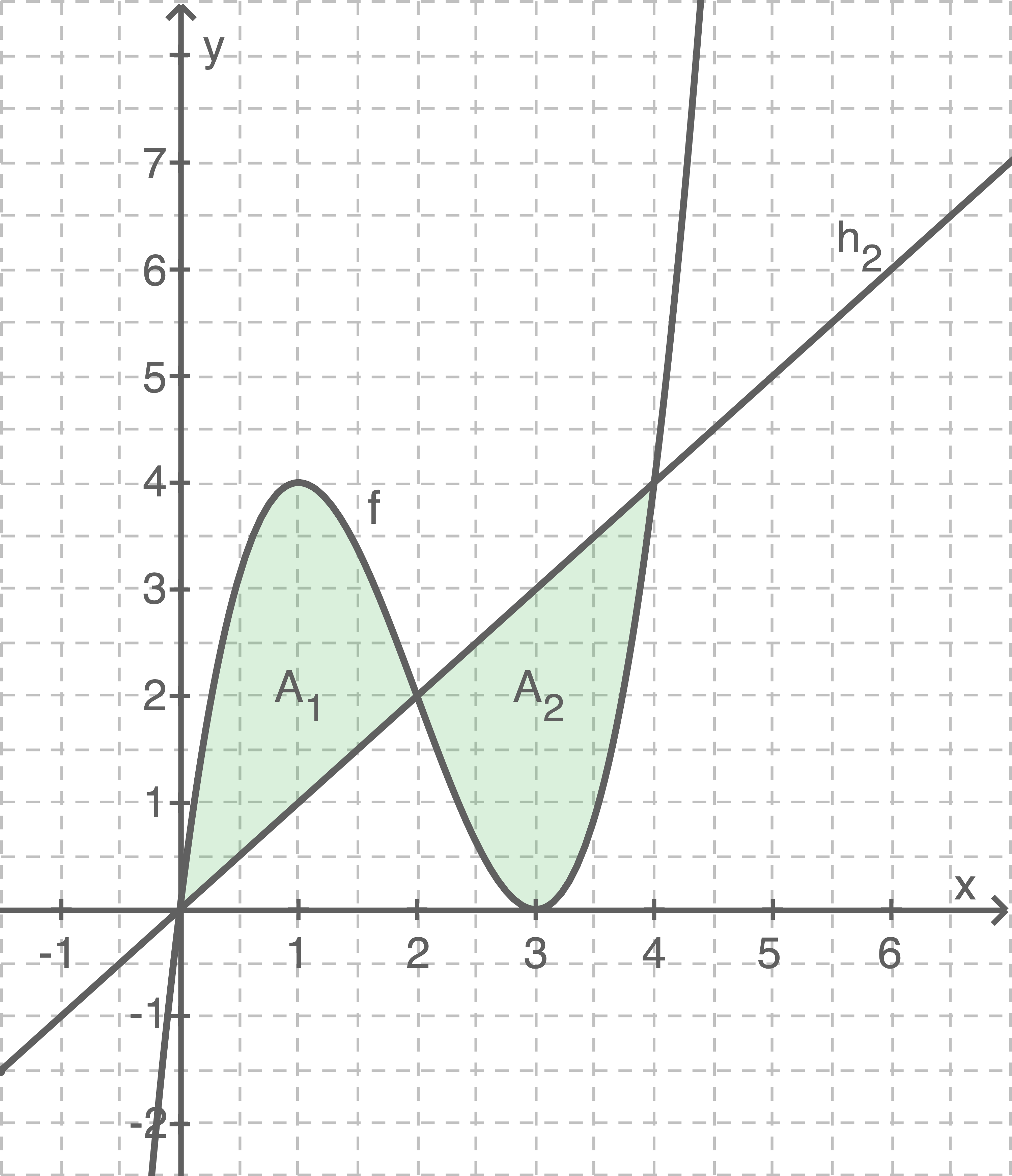 Aus der Abbildung lassen sich die Schnittpunkte der Graphen der Funktionen
Aus der Abbildung lassen sich die Schnittpunkte der Graphen der Funktionen  und
und  ablesen:
ablesen:
 ,
,  und
und  Es folgt:
Die gesamte eingeschlossene Fläche ergibt sich nun durch
Es folgt:
Die gesamte eingeschlossene Fläche ergibt sich nun durch ![\(A= 2\cdot A_1 = 8 \; \,\text{[FE]}.\)](https://www.schullv.de/resources/formulas/ab7dea7ea7e58a2286f1d4bb08fb00a2f4c07d0b6a8a8579514835ecfc36a817_light.svg)

4.
Term nachweisen
Aus der Aufgabenstellung lassen sich die Koordinaten der drei Eckpunkte des Dreiecks  in Abhängigkeit von
in Abhängigkeit von  herauslesen:
herauslesen:


 Das Dreieck kann also beispielsweise wie folgt angeordnet sein:
Das Dreieck kann also beispielsweise wie folgt angeordnet sein:
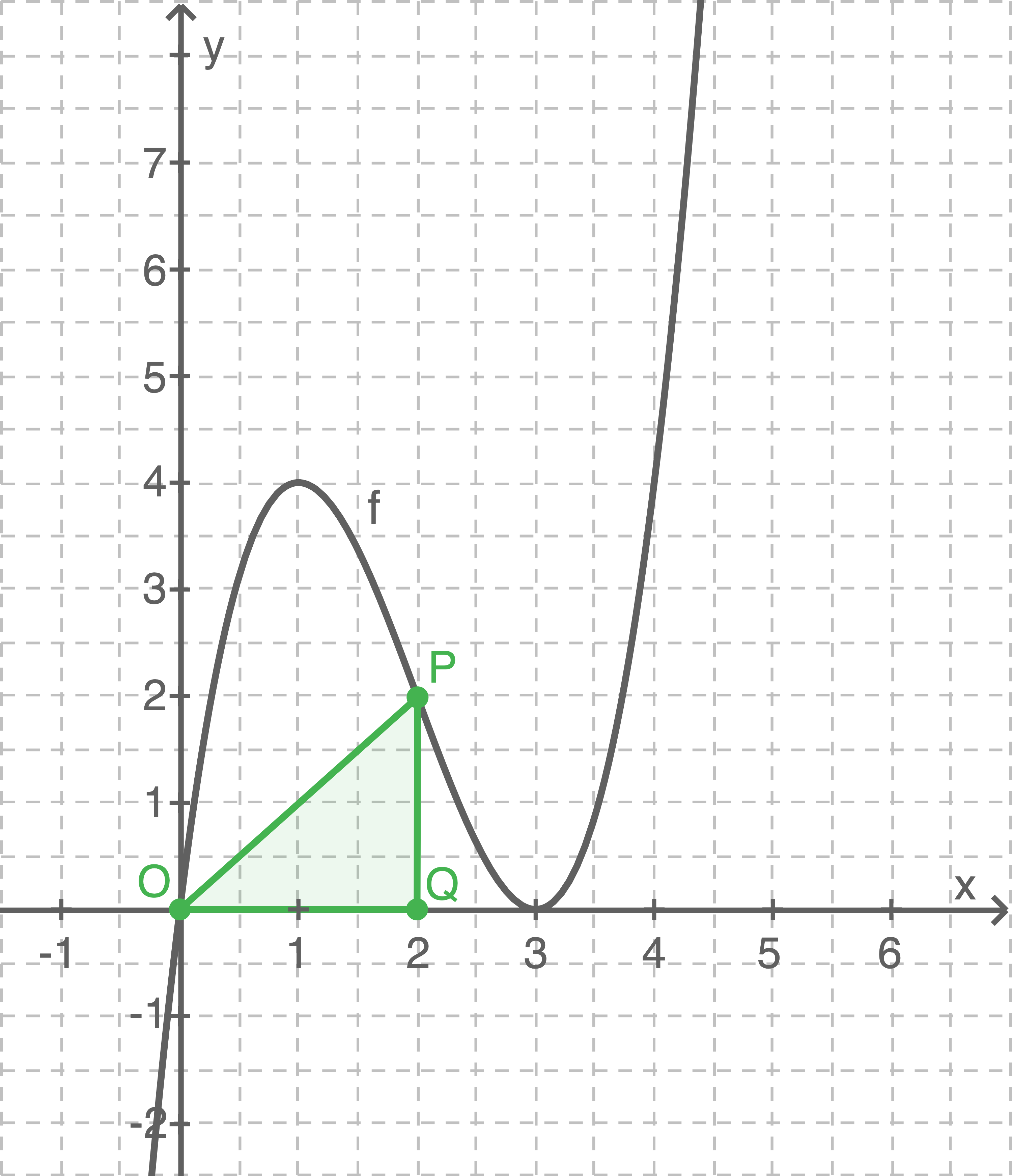 Da
Da  senkrecht über
senkrecht über  liegt, handelt es sich bei
liegt, handelt es sich bei  um ein rechtwinkliges Dreieck.
Für den Flächeninhalt
um ein rechtwinkliges Dreieck.
Für den Flächeninhalt  von
von  folgt:
folgt:
![\(\begin{array}[t]{rll}
A(u) &=& \dfrac{1}{2}\cdot u \cdot f(u) \\[5pt]
&=& \dfrac{1}{2} \cdot u \cdot (u^3-6u^2+9u) \\[5pt]
&=& \dfrac{1}{2}\cdot (u^4-6u^3+9u^2) \\[5pt]
&=& \dfrac{1}{2}\cdot u^4-3\cdot u^3+\dfrac{9}{2}\cdot u^2 \\[5pt]
&=& B(u)
\end{array}\)](https://www.schullv.de/resources/formulas/fea7fcedd6afba315fa15b4d116b57809d28e1419e699f634bb2bf5db53716e1_light.svg) Extremfälle ermitteln
1. Schritt: Ableitungen bestimmen
Extremfälle ermitteln
1. Schritt: Ableitungen bestimmen
![\(\begin{array}[t]{rll}
B(u) &=&\dfrac{1}{2}u^4-3u^3+\dfrac{9}{2}u^2 \\[5pt]
B](https://www.schullv.de/resources/formulas/1c333ec41169aef77b02890acb6110a2feede0ea4116785ecd6a089ab17270c1_light.svg) 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
B‘(u) &=&0 &\quad \scriptsize \\[5pt]
2u^3 - 9u^2+9u &=& 0&\quad \scriptsize \\[5pt]
u \cdot \left(u^2 - \dfrac{9}{2}u+\dfrac{9}{2} \right)&=& 0 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2fb02bb6be15675d9e1ea4f41d2317d42556d0e8ec61e3940602ae38f4ce393e_light.svg) Mit dem Satz vom Nullprodukt folgt:
Mit dem Satz vom Nullprodukt folgt:
 und
und  Mit der pq-Formel ergibt sich:
Mit der pq-Formel ergibt sich:
![\(\begin{array}[t]{rll}
u_{2,3}&=& -\left(-\dfrac{9}{4}\right)\pm\sqrt{\left(-\dfrac{9}{4}\right)^2-\dfrac{9}{2}} \\[5pt]
u_{2,3}&=& \dfrac{9}{4}\pm\sqrt{\dfrac{81}{16}-\dfrac{72}{16}} \\[5pt]
u_{2,3}&=& \dfrac{9}{4}\pm\sqrt{\dfrac{9}{16}} \\[5pt]
u_{2,3}&=& \dfrac{9}{4}\pm\dfrac{3}{4} \\[5pt]
u_2&=& 3 \\[5pt]
u_3&=& \dfrac{3}{2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a24f6905e11e03328b74d98fa7594d6568f64afe340060e16567f2d32f48d37a_light.svg) 3. Schritt: Hinreichendes Kriterium für Extremstellen anwenden
3. Schritt: Hinreichendes Kriterium für Extremstellen anwenden
![\(\begin{array}[t]{rll}
B](https://www.schullv.de/resources/formulas/067124523cbd4b22ab31255eb8c82a5f9574d570409ecd3108a8d94ee561b5c6_light.svg)
![\(\begin{array}[t]{rll}
B](https://www.schullv.de/resources/formulas/d7f0b1f2eb1d1159fd3dd5ba4f05117eabf4efa47aeb9a77892d36570b357b6b_light.svg)
![\(\begin{array}[t]{rll}
B](https://www.schullv.de/resources/formulas/ae611594a42c83aa57f803ef43f295d63fcdc636259f5dd63c8be477a30cec8a_light.svg) Somit besitzt der Graph von
Somit besitzt der Graph von  zwei Tiefpunkte an den Stellen
zwei Tiefpunkte an den Stellen  und
und  und einen Hochpunkt an der Stelle
und einen Hochpunkt an der Stelle  4. Schritt: Funktionswerte bestimmen
4. Schritt: Funktionswerte bestimmen
![\(\begin{array}[t]{rll}
B(0)&=& \dfrac{1}{2} \cdot 0^4-3 \cdot 0 ^3+\dfrac{9}{2} \cdot 0^2 & \\[5pt]
&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/7c6029c2d0f94d908239dacb5f93cd68c7a0ad8eafadabd762b4c7df38cb69dc_light.svg)
![\(\begin{array}[t]{rll}
B(3)&=& \dfrac{1}{2} \cdot 3^4-3 \cdot 3 ^3+\dfrac{9}{2} \cdot 3^2 & \\[5pt]
&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/afdb396c7514a6053c95d18d4f83dc318393b3f22a4855225c31f2abee511416_light.svg) Für
Für  entspricht das Dreieck
entspricht das Dreieck  einem einzelnen Punkt im Ursprung. Für
einem einzelnen Punkt im Ursprung. Für  besitzen die Punkte
besitzen die Punkte  und
und  dieselben Koordinaten und es ergibt sich die Strecke
dieselben Koordinaten und es ergibt sich die Strecke  Somit ist der maximale Flächeninhalt des Dreiecks
Somit ist der maximale Flächeninhalt des Dreiecks  gegeben durch
gegeben durch ![\(B(1,5)=2,53\,\text{[FE]}.\)](https://www.schullv.de/resources/formulas/b8e70e4adbe703ad11c83c2c0980b3098d029a7154637b51ffce34ae33d32fad_light.svg)

Hilfsskizze