A2 - Analysis

Eine Gärtnerei vertreibt ein tunnelförmiges Foliengewächshaus, dessen Bodenfläche $12\;\text{m}$ lang und $7\;\text{m}$ breit ist und dessen Höhe $3\;\text{m}$ beträgt (Material 1).

Ermittle die Funktionsgleichung einer quadratischen Funktion $p,$ deren Graph die parabelförmige Berandung der vorderen Abschlussfläche des Gewächshauses beschreibt.

Rechenweg anzeigen

$\left[\text{zur Kontrolle:} \; p(x) = \; ...\right]$

(7 BE)

2.1

Berechne das gesamte Volumen des Gewächshauses unter der Annahme, dass die vordere und hintere Abschlussfläche senkrecht auf der Bodenfläche stehen.

(8 BE)

2.2

Um eine geeignete Arbeitshöhe für die Gärtner zu bekommen, wird in einer Hälfte des Gewächshauses in 1 Meter Höhe über die gesamte Länge des Gewächshauses ein Zwischenboden eingefügt (Material 2).
Ermittle den Flächeninhalt des Zwischenbodens.
Berechne, um wie viel Prozent der Zwischenboden kleiner ist als die Bodenfläche dieser Gewächshaushälfte.

(7 BE)

Mehrere Kunden reklamieren, dass das Gewächshaus im oberen Bereich zu eng gebaut sei. Die Firma möchte mit einer Halbkreis-Form Abhilfe schaffen (Material 3). Die Höhe und die Länge des Gewächshauses sollen beibehalten werden.

3.1

Bestimme den Verbrauch an Folie für die neue Bedachung (ohne Vorder- und Rückseite).

(4 BE)

3.2

Leite ausgehend von den Informationen in Material 3 die Funktionsgleichung einer Funktion $k$ her, mit deren Graph der Rand der halbkreisförmigen vorderen Abschlussfläche des Gewächshauses beschrieben werden kann.

Rechenweg anzeigen

$\left[\text{zur Kontrolle:} \; k(x) = \; ...\right]$

(5 BE)

3.3

Um im unteren Bereich mehr Breite zu gewinnen, wird der Kreisbogen ab den Punkten $P_1(-2,5\mid k(-2,5))$ und $P_2(2,5\mid k(2,5))$ durch Tangenten ersetzt.
Berechne die neue Breite der Bodenfläche des Gewächshauses.
Hinweis: Du kannst einfache geometrische Beziehungen zwischen Kreisradius und Kreistangente nutzen.

(9 BE)

Material 1

Material 2

Material 3

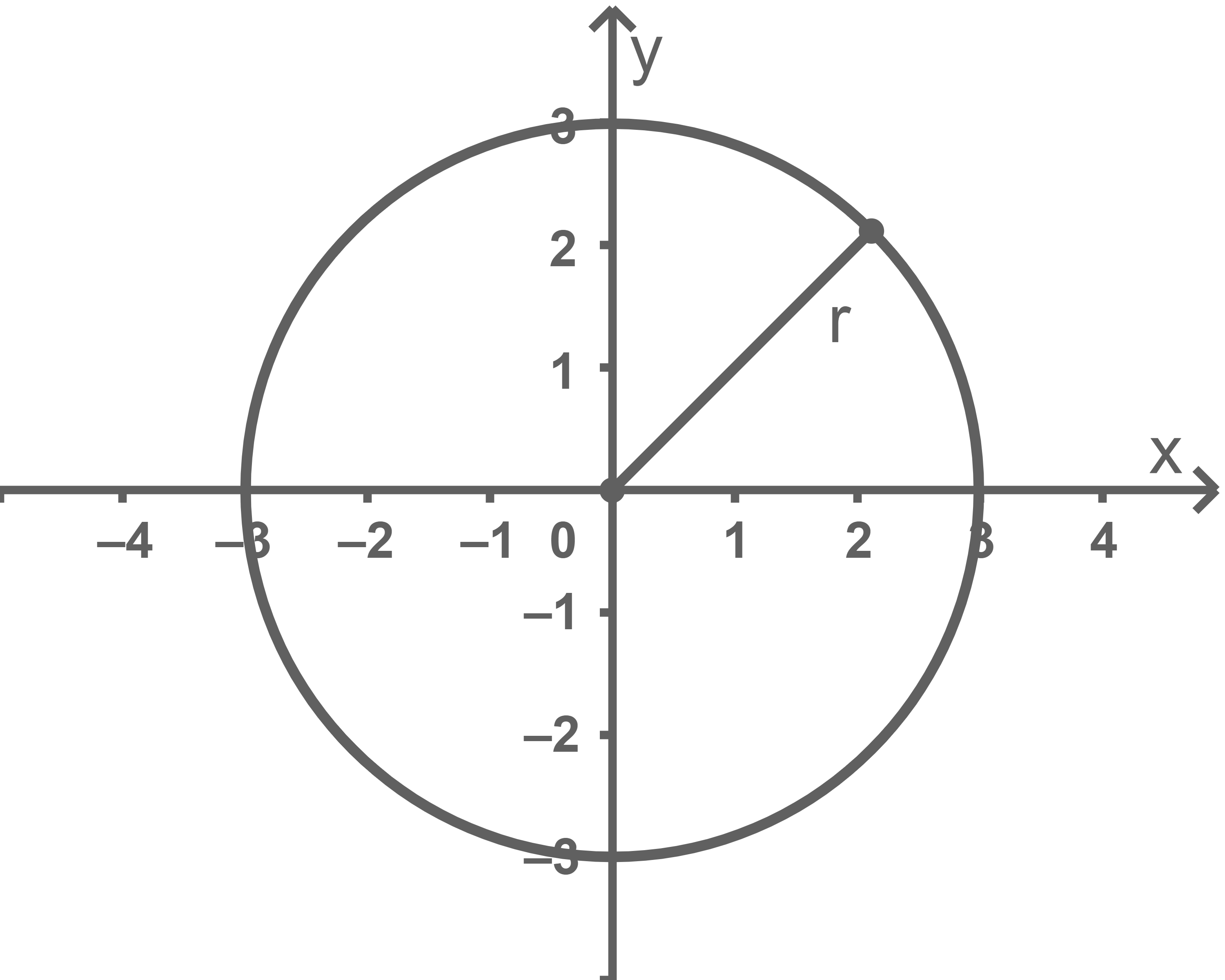
Information: Die Gleichung $x^2 +y^2=r^2$ beschreibt einen Kreis mit dem Radius $r$ , dessen Mittelpunkt im Nullpunkt des Koordinatensystems liegt.

Mit Hilfe der $x$ -Achse als Boden und der $y$ -Achse in der Mitte des Durchschnittes des Gewächshaueses, wobei eine Längeneinheit einem Meter entspricht, ergeben sich aus der Aufgabenstellung folgende drei Gleichungen für die allgemeine Funktionsgleichung $p(x)=a \cdot x^2 + b\cdot x +c:$

$\begin{array}[t]{rll} p\left(-\dfrac{7}{2}\right)&=& 0 \\[5pt] p\left(\dfrac{7}{2}\right)&=& 0 \\[5pt] p(0)&=& 3 \end{array}$

Aufstellen eines linearen Gleichungssystems liefert:

$\begin{array}{} \text{I}\quad& \left(-\dfrac{7}{2} \right)^2 \cdot a- \dfrac{7}{2} \cdot b + c &=& 0 \\ \text{II}\quad& \left(\dfrac{7}{2} \right)^2 \cdot a + \dfrac{7}{2} \cdot b + c &=& 0 \\ \text{III}\quad& 0^2 \cdot a + 0 \cdot b + c &=& 3 \\ \end{array}$

Gleichung $\text{III}$ liefert direkt $c=3.$ Addition von $\text{I}$ und $\text{II}$ und Einsetzen von $c$ liefert weiter:

Rechenweg anzeigen

$a \approx -0,245$

Durch Einsetzen von $a= -\dfrac{12}{49}$ und $c=3$ in Gleichung $\text{I}$ folgt weiterhin:

Rechenweg anzeigen

$b = 0$

Die Funktion $p$ ist also gegeben durch $p(x)$ $= a$ $\cdot x^2$ $+ b\cdot x$ $+ c$ $= -\dfrac{12}{49}$ $\cdot x^2$ $+3,$ wobei $x$ im Intervall $[-3,5 ; 3,5]$ liegt und eine Längeneinheit einem Meter entspricht.

2.1

Das gesamte Volumen des Gewächshauses ergibt sich durch Multiplikation des Flächeninhaltes der Vorderfläche mit der Länge des Gewächshauses. Für den Flächeninhalt der Vorderfläche ergibt sich:

Rechenweg anzeigen

$A = 14 \;[\text{m}^2]$

Damit folgt für das gesamte Volumen des Gewächshauses:

$V_{\text{gesamt}}$ $= 12$ $\cdot A$ $= 12$ $\cdot 14$ $= 168 \;[\text{m}^3]$

2.2

1. Schritt: Fläche des Zwischenbodens berechnen

Die Fläche des Zwischenbodens hat die Form eines Rechtecks. Die Breite ergibt sich durch den $x$ -Wert der in Material 2 dargestellten Schnittstelle der Geraden $y=1$ mit der Parabel:

Rechenweg anzeigen

$x_{1,2} = \pm \dfrac{7}{\sqrt{6}}$

Da der Zwischenboden in der Skizze rechts von der $y$ -Achse liegt, ist $x_1 = \dfrac{7}{\sqrt{6}}$ die gesuchte $x$ -Koordinate. Für die Breite folgt:

$\dfrac{7}{\sqrt{6}}$ $- 0$ $= \dfrac{7}{\sqrt{6}}$ $\approx 2,86 \;[\text{m}]$ .

Für den Flächeninhalt des Zwischenbodens folgt damit insgesamt:

$A_{\text{Zwischenboden}}$ $= \dfrac{7}{\sqrt{6}}$ $\cdot 12$ $= \dfrac{7 \cdot 2 \cdot 6}{\sqrt{6}}$ $= 14$ $\cdot \sqrt{6}$ $\approx 34,3 \;[\text{m}^2].$

2. Schritt: Flächeninhalt der Bodenfläche der Gewächshaushälfte berechnen

Mit einer Länge von $12 \; \text{m}$ und einer Breite von $3,5 \text{ m}$ folgt für den Flächeninhalt der Bodenflächenhälfte:

$A_{\text{Bodenflächenhälfte}}$ $= 12 \text{ m}$ $\cdot 3,5 \text{ m}$ $= 42 \text{ m}^2.$

3. Schritt: Prozentuale Abweichung berechnen

$\dfrac{A_{\text{Zwischenboden}}}{A_{\text{Bodenflächenhälfte}}}$ $= \dfrac{34,3 \text{ m}^2}{42 \text{ m}^2}$ $\approx 0,82.$

Der Zwischenbodenflächeninhalt misst damit ca. $82 \text{ %}$ der Bodenfläche der Gewächshaushälfte. Somit ist der Zwischenboden etwa $100\text{ %} - 82\text{ %} = 18 \text{ %}$ kleiner.

3.1

Die Folienverbrauch für die Bedachung berechnet sich mit Hilfe der Länge des Gewächshauses von $12 \text{ m}$ und dem Umfang des Querschnitts des Gewächshauses, einem Halbkreis. Aus dem Radius $r=3$ folgt:

Rechenweg anzeigen

$u_{\text{Halbkreis}}\approx 9,42$

Der Verbrauch an Folie für die neue Bedachung beträgt damit $12 \text{ m} \cdot 9,42 \text{ m} \approx 113,04 \text{ m}^2$ .

3.2

Da $x^2 + y^2 = r^2$ einen Kreis mit Radius $r$ mit dem Nullpunkt als Mittelpunkt beschreibt, ergibt sich $k(x),$ wenn die obere Kreishälfte als vordere Abschlussfläche angenommen wird, durch Einsetzen von $r=3$ und Umformen nach $y$ wie folgt:

$\begin{array}{rll} x^2 + y^2 &=& r^2 &\quad \scriptsize \mid \; -x^2 \\[5pt] y^2 &=& r^2 -x^2 &\quad \scriptsize \mid \; \sqrt{\;} \\[5pt] \left|y\right| &=&\sqrt{r^2 -x^2} \\[5pt] \left|y\right| &=& \sqrt{3^2 -x^2} \\[5pt] y &=&\sqrt{9 -x^2} \end{array}$

Damit beschreibt $k(x) = \sqrt{9 -x^2}$ für $-3\leq x\leq 3$ die vordere Abschlussfläche des Gewächshauses.

3.3

Folgende Skizze hilft beim Verständnis:

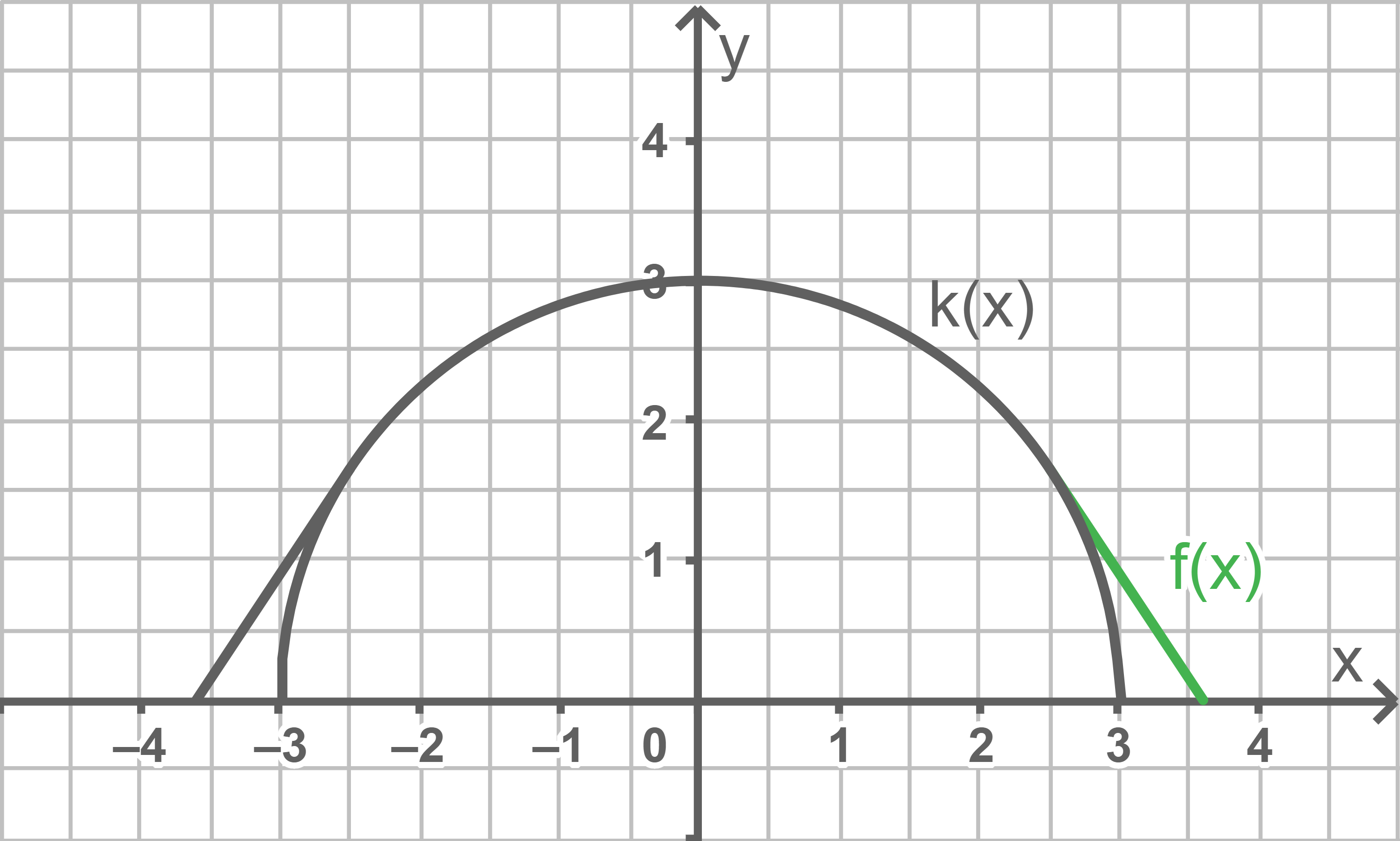Aus der Achsensymmetrie des Kreisbogens bezüglich der $y$ -Achse folgt, dass die halbe Breite der $x$ -Wert der Nullstelle der eingezeichneten Tangente $f$ ist.

1. Schritt: Steigung des Kreisradius in $P\left(2,5 \mid k(2,5) \right)$ bestimmen

Berechnung des Funktionswertes von $k(x)$ an der Stelle $x=2,5$ liefert:

Rechenweg anzeigen

$k(2,5) = \dfrac{\sqrt{11}}{2}$

Die Steigung des Kreisradius in $P\left(2,5 \mid \dfrac{\sqrt{11}}{2}\right)$ ergibt sich dann wie folgt:

$\dfrac{\left(\frac{\sqrt{11}}{2}\right)}{2,5}$ $= \dfrac{\sqrt{11}}{5}.$

2. Schritt: Steigung $m_x$ der Tangente $f$ bestimmen

Da die Tangente senkrecht zum Kreisradius steht, ergibt sich die Steigung $m_x$ der Tangenten $f$ als negativer Kehrwert der Steigung des Kreisradius: