Hyperbeln

Die Graphen von Potenzfunktionen, die einen negativen Exponenten haben, werden Hyperbeln genannt. Sie bestehen aus zwei zueinander symmetrischen Hyperbelästen.

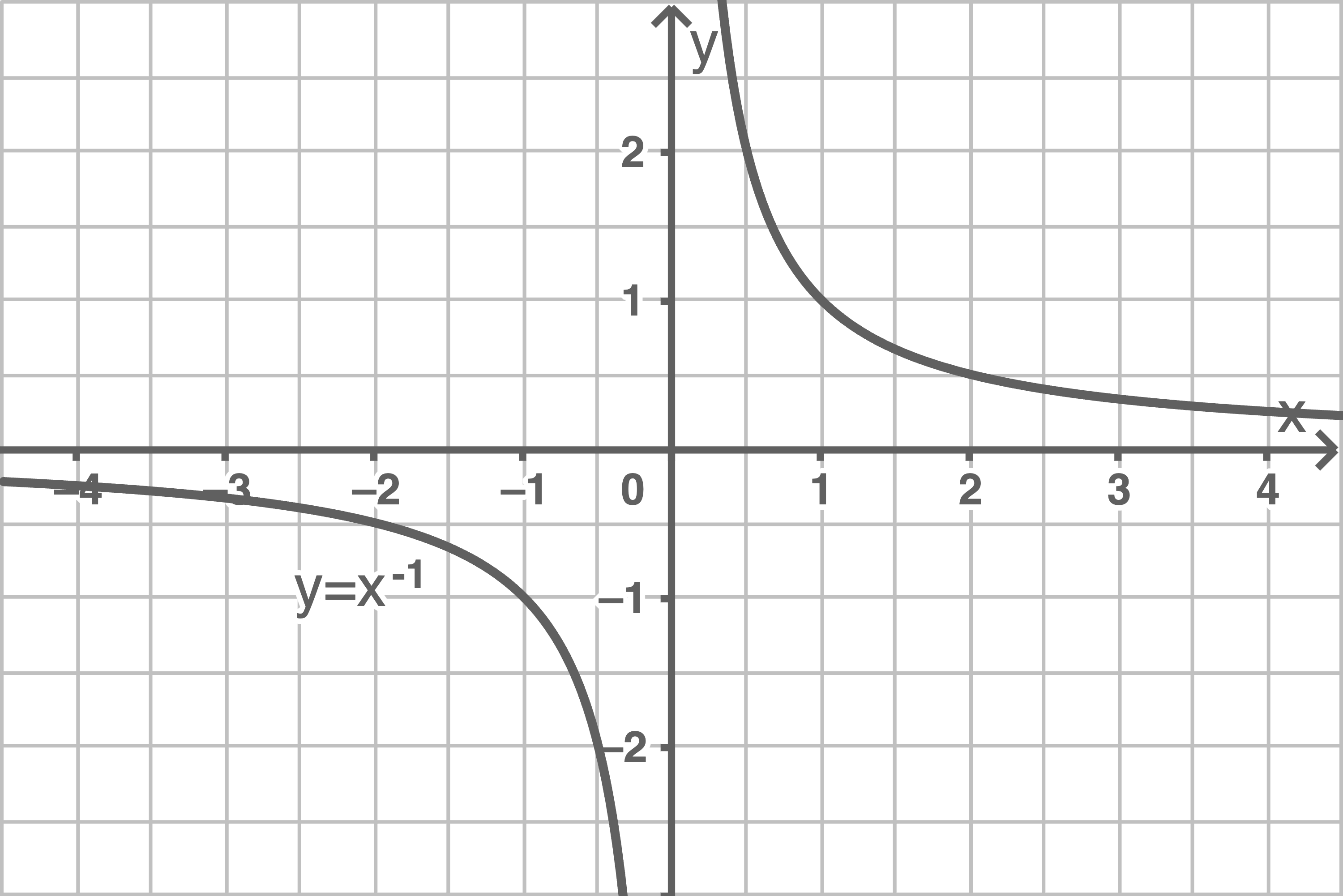
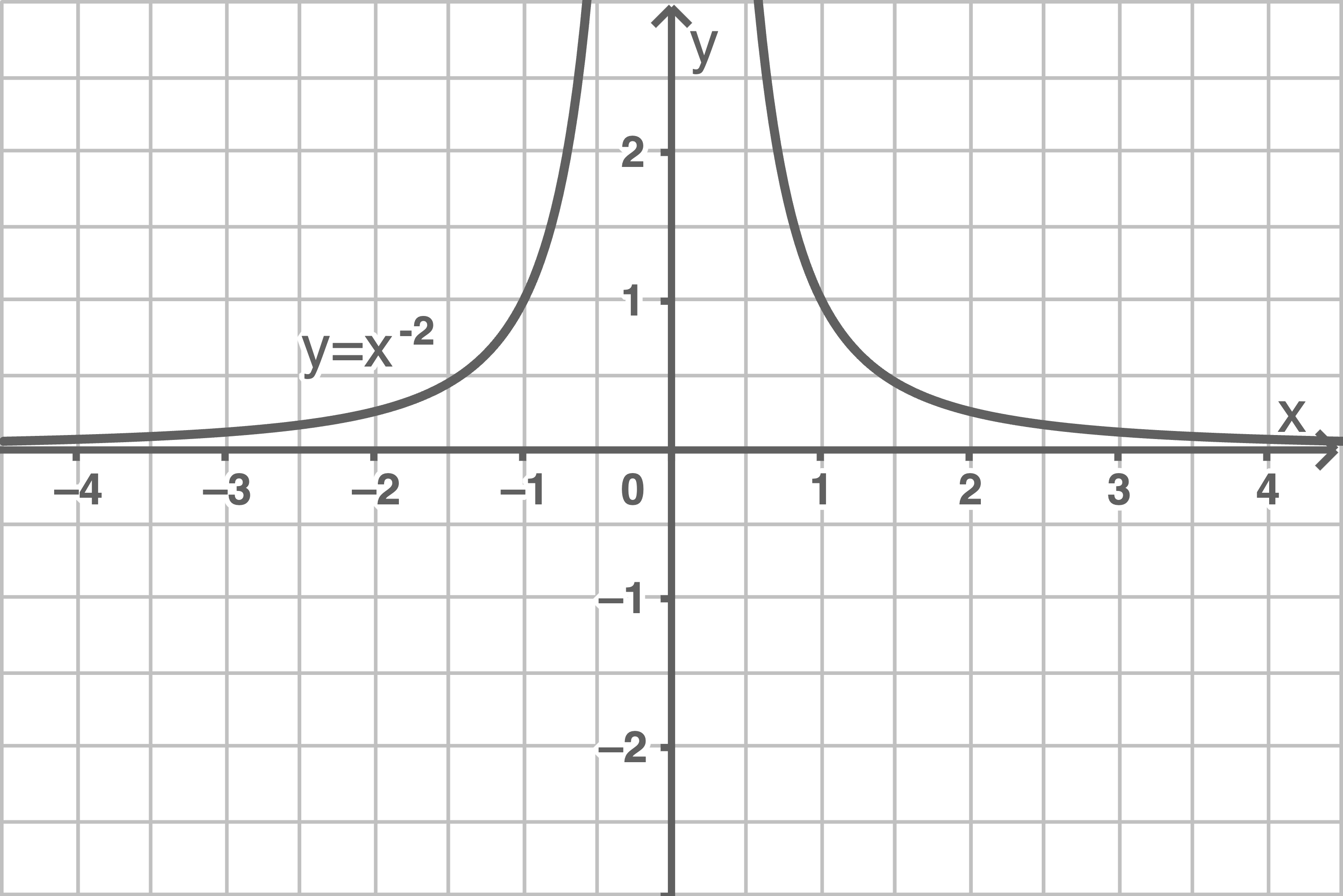
Hyperbel Sachsen Anhalt Mathe Sekundarschule

Für die Hyperbeln der Funktionen $y=x^{-1}$ und $y=x^{-2}$ mit dem Definitionsbereich $\mathbb{R} \backslash\{0\}$ gilt:

Für sehr große und sehr kleine Werte für $x$ nähern sich die Graphen der $x$ -Achse an, erreichen oder überschreiten diese jedoch nie.

Beide Funktionen haben keine Nullstelle.

Beide Graphen verlaufen durch den Punkt $P(1 \mid 1).$

Der Graph der Funktion mit $y=x^{-2}$ ist achsensymmetrisch zur $y$ -Achse, während der Graph der Funktion $y=x^{-1}$ punktsymmetrisch zum Koordinatenursprung ist.

Beide Teilgraphen zu $y=x^{-1}$ sind fallend. Der Graph zu $y=x^{-2}$ steigt für $x\lt0$ und fällt für $x\gt0.$

Der Wertebereich der Funktion $y=x^{-1}$ ist $\mathbb R\backslash\{0\}.$ Zum Wertebereich der Funktion $y=x^{-2}$ gehören alle positiven reellen Zahlen.

Hyperbeln

Weiter lernen mit SchulLV-PLUS!

Weiter lernen mit SchulLV-PLUS!