Lineare und exponentielle Abnahme
Lineare Abnahme
Innerhalb gleicher Zeitintervalle nimmt der Bestand jeweils um den gleichen Betrag ab (Abnahmebetrag). Beispiel: Eine Kerze ist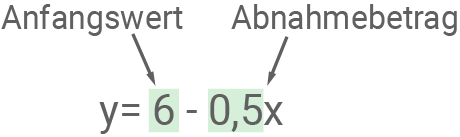
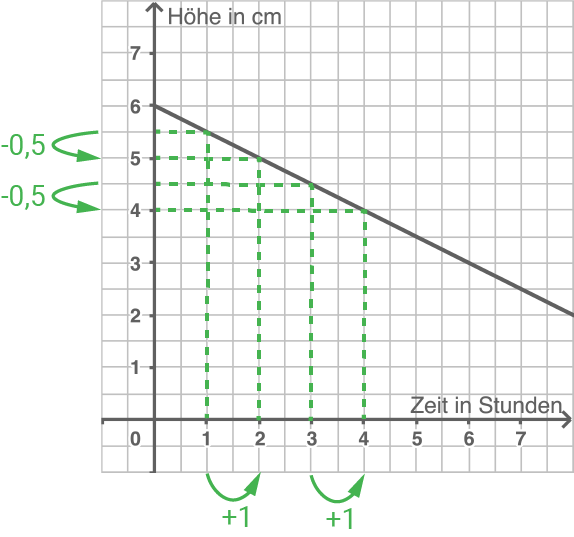
Exponentielle Abnahme
Innerhalb gleicher Zeitintervalle nimmt der Bestand mit konstanter Zerfallsrate ab. Die Größe wird immer mit dem gleichen Faktor kleiner 1 multipliziert (Abnahmefaktor). Beispiel: Eine Patientin nimmt einmalig
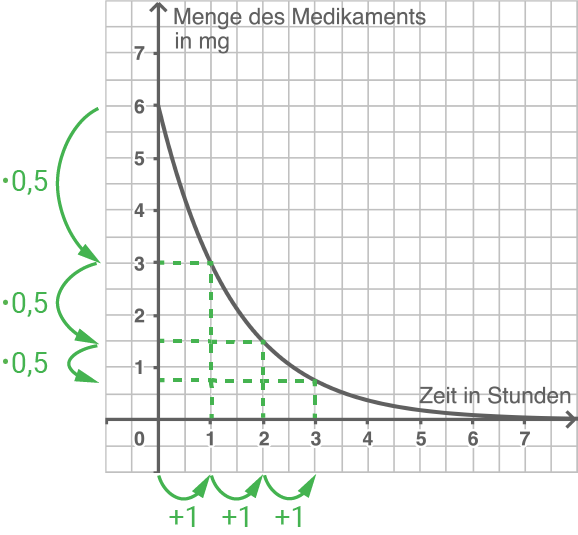
Bestimmung des Abnahmefaktors
Handelt es sich um eine exponentielle Abnahme, so gilt für den Abnahmefaktor 
und die Abnahmerate 
Nimmt der Anfangswert also pro Zeitintervall um die Rate 
ab, so wird mit dem Faktor 
multipliziert.
1
Ordne zu, ob es sich um lineare oder exponentielle Abnahme handelt.
a)
Die Temperatur eines Kaffees nimmt pro Minute um 
ab.
b)
Die Populationsgröße einer bedrohten Tierart halbiert sich alle 5 Jahre.
c)
Die Batterieanzeige eines Mobiltelefons sinkt pro Stunde um 5 Prozentpunkte.
d)
Der Wasserstand in einem See sinkt pro Monat um 1 Meter.
e)
Die Menge an verbleibendem Kraftstoff in einem Tank verringert sich um 7 Liter pro 100 gefahrene Kilometer.
f)
Die Helligkeit eines LED-Lichts verringert sich um 
pro Stunde.
g)
Die Konzentration eines Pestizids im Boden nimmt aufgrund von Umweltschutzmaßnahmen um 
pro Jahr ab.
h)
Die Höhe eines Luftballons verringert sich um 2 Zentimeter pro Stunde aufgrund von Luftaustritt.
2
Eine Autovermietung besitzt Mietwagen, die durch Abnutzung jedes Jahr an Wert verlieren. Bei der Ermittlung des Vermögens des Unternehmens wird auch der Wert der Mietwagen berechnet. Dazu gibt es zwei verschiedene Methoden zur Berechnung des Wertverlusts:
- Der Wert einer Maschine verliert jedes Jahr
der Anschaffungskosten.
- Der Wert einer Maschine verliert jedes Jahr
des Wertes vom Vorjahr, im 1. Jahr
a)
Eine Maschine kostet 
Nach wie viel Jahren ist der Restwert 
Lege für beide Berechnungsmethoden jeweils eine Tabelle an.
b)
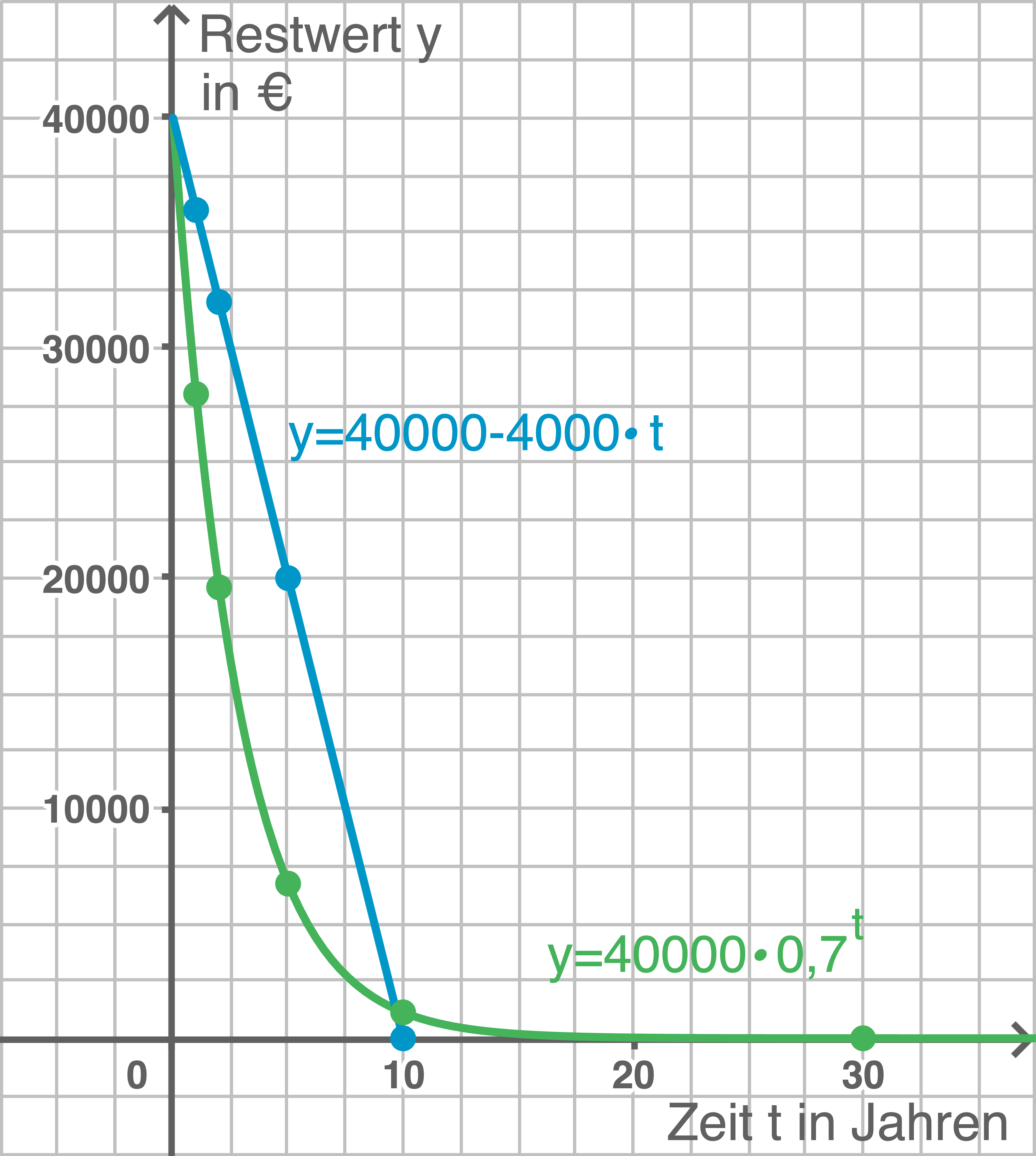
Stelle die beiden Methoden als Graphen und Funktionsgleichungen dar.
Zeichne dazu für beide Berechnungsmethoden die Graphen der Funktion Zeit t (in Jahren) 
Restwert 
( in 
) in ein Koordinatensystem.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Lineare Abnahme
b)
Exponentielle Abnahme
c)
Lineare Abnahme
d)
Lineare Abnahme
e)
Lineare Abnahme
f)
Exponentielle Abnahme
g)
Exponentielle Abnahme
h)
Lineare Abnahme
2
a)
1. Methode:
der Anschaffungskosten entsprechen 
Es folgt also:
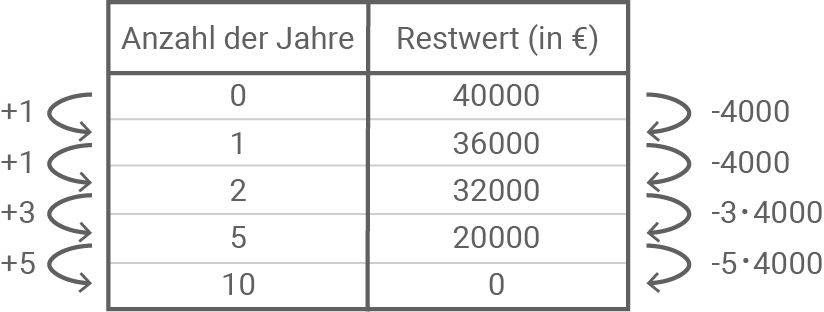Der Restwert 
wird somit nach 10 Jahren erreicht.
2. Methode:
Die Anschaffungskosten nehmen jedes Jahr mit der Rate 
ab. Für den Abnahmefaktor gilt also:
Es folgt somit:
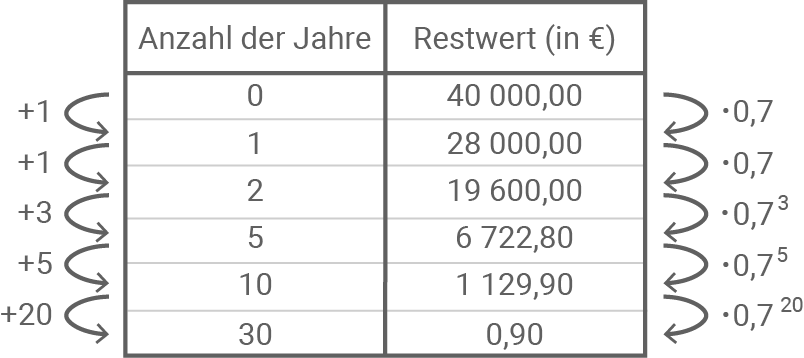Selbst nach 30 Jahren hat der Mietwagen noch nicht den vollständigen Wert verloren, obwohl der Restwert immer weiter sinkt.
b)
1. Methode
Der Mietwagen verliert pro Jahr den festen Wert 
, der Restwert nimmt somit linear ab.
Mit dem Anfangswert 
und dem Abnahmebetrag ergibt sich in Abhängigkeit von der Zeit 
in Jahren folgende Funktionsgleichung:
2. Methode
Der Wert des Mietwagens nimmt anfangs sehr schnell ab, sinkt dann aber immer langsamer. Es handelt sich somit um exponentielle Abnahme.
Ebenso fällt auch der Graph anfangs stark und nähert sich dann immer langsamer der -Achse, wobei diese nie erreicht oder überschritten wird. Der Restwert wird folglich nie erreicht.
Mit dem Anfangswert und dem Abnahmefaktor 
ergibt sich in Abhängigkeit von der Zeit in Jahren folgende Funktionsgleichung:
