Lineare und exponentielle Zunahme
Lineare Zunahme
Innerhalb gleicher Zeitintervalle nimmt der Bestand jeweils um den gleichen Betrag zu (Zunahmebetrag). Beispiel: In einer Stadt wurden bereits 3 Kilometer Fahrradweg ausgebaut. Jeden Tag werden weitere 500 Meter asphaltiert.
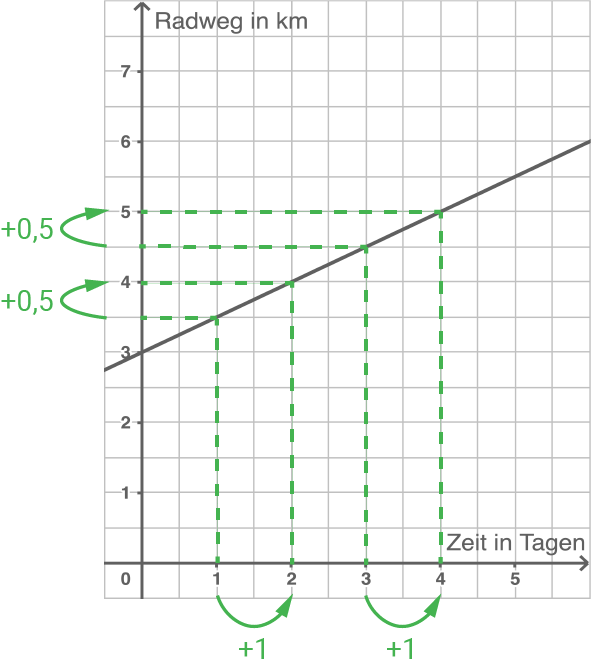
Exponentielle Zunahme
Innerhalb gleicher Zeitintervalle wächst der Bestand mit konstanter Wachstumsrate. Die Größe wird immer mit dem gleichen Faktor größer 1 vervielfacht (Zunahmefaktor). Beispiel: In einer Stadt sind 100 Einwohner bereits mit einer Infektionskrankheit infiziert. Die Anzahl der Infizierten verdoppelt sich täglich.
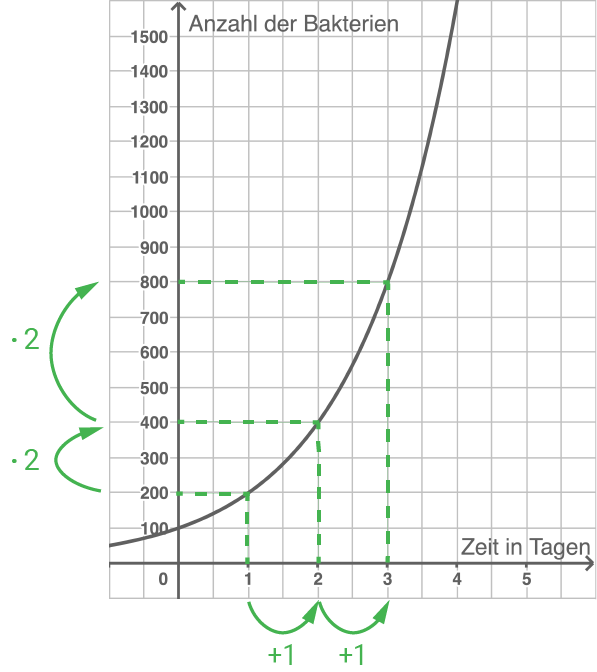
Bestimmung des Zunahmefaktors
Handelt es sich um eine exponentielle Zunahme, so gilt für den Zunahmefaktor 
und die Zunahmerate 
Nimmt der Anfangswert also pro Zeitintervall um die Rate 
zu, so wird mit dem Faktor 
multipliziert.
1
Ordne zu, ob es sich um lineare oder exponentielle Zunahme handelt.
a)
Die Anzahl der Salmonellen verdoppelt sich jeden Tag.
b)
Pro 10 Meter Tiefe nimmt der Wasserdruck im Meer um ein Bar zu.
c)
Ein Huhn legt alle zwei Tage ein Ei.
d)
Eine Pflanze wächst täglich um 5 Millimeter.
e)
Die Anzahl der Infizierten steigt wöchentlich um 
f)
Die Temperatur in einem Raum steigt stündlich um 1,2 Grad.
g)
Die Ausdehnung eines Gases in einem abgeschlossenen Behälter verdreifacht das Volumen alle 5 Minuten.
h)
Ein landwirtschaftlicher Betrieb hat einen Futtervorrat von 8 Tonnen. Jeden Tag werden zusätzliche 300 Kilogramm Futter produziert.
2
Bei Baggerarbeiten wächst ein Baggersee von 
Größe jede Woche um 
Eine Algenart bedeckt zu Beginn der Baggerarbeiten 
Wasserfläche. Die mit Algen bedeckte Fläche verdreifacht sich jede Woche.
a)
Lege für die Zunahme der Wasserfläche und für die Zunahme der Algenfläche eine Tabelle für die ersten 6 Wochen an.
Übertrage die Werte in ein geeignetes Koordinatensystem und beschreibe das Wachstum.
b)
Erkläre mit Hilfe der skizzierten Graphen und der Tabellen, nach wie viel Wochen die gesamte Wasseroberfläche von den Algen bedeckt ist.
c)
Stelle für die Zunahme der Wasserfläche und für die Zunahme der Algenfläche jeweils eine Funktionsgleichung auf.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Exponentielle Zunahme
b)
Lineare Zunahme
c)
Lineare Zunahme
d)
Lineare Zunahme
e)
Exponentielle Zunahme
f)
Lineare Zunahme
g)
Exponentielle Zunahme
h)
Lineare Zunahme
2
a)
Tabellen anlegen
Zunahme der Wasserfläche:
Zunahme der Algenfläche:
Graphen skizzieren
Wasserfläche
Algenfläche
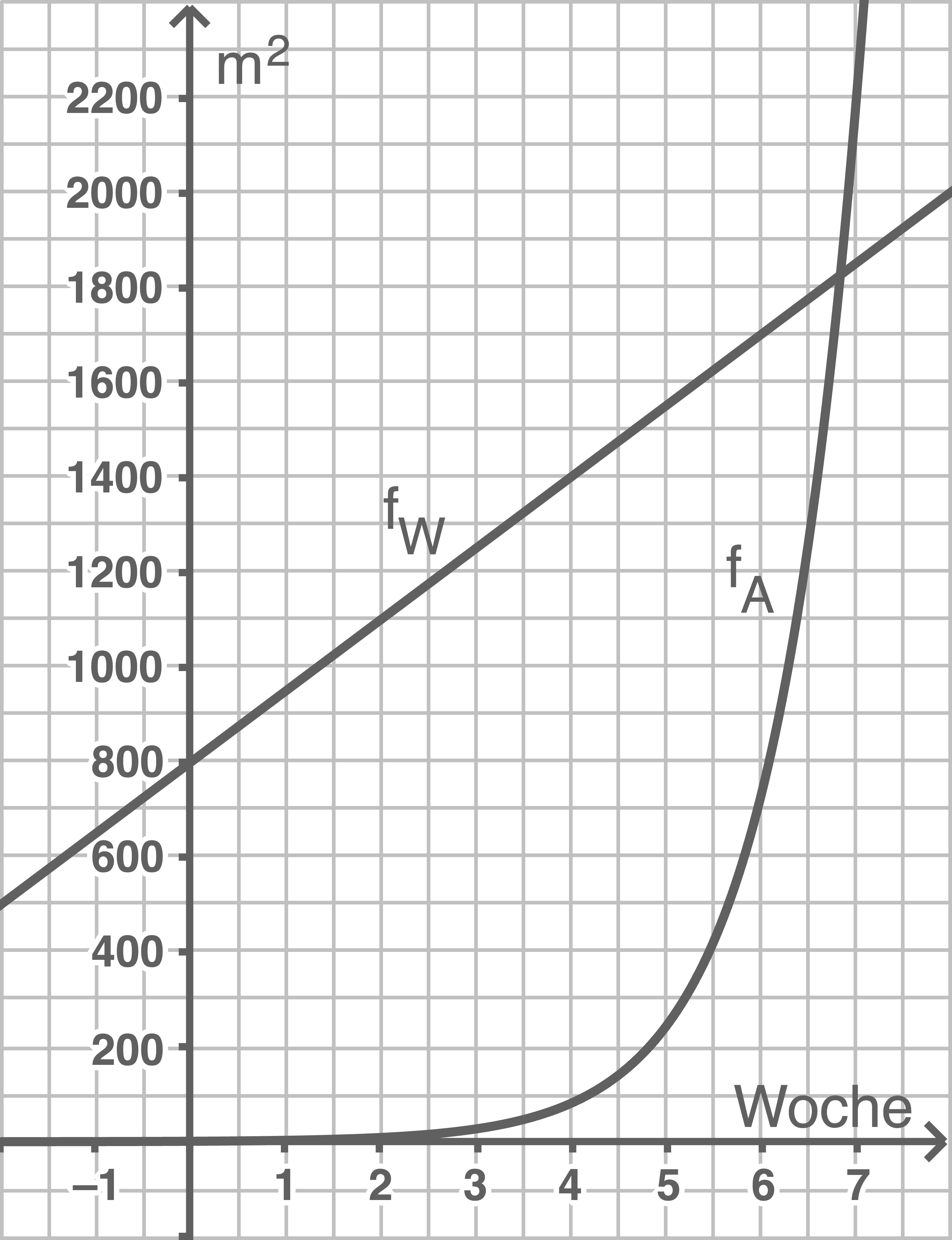Wachstum beschreiben
Die Fläche des Baggersees nimmt pro Woche jeweils um den gleichen Betrag von 
zu, der Graph steigt folglich konstant. Es handelt sich hierbei also um lineare Zunahme.
Die Fläche des Algenteppichs verdreifacht sich, nimmt also pro Woche um den Faktor 3 zu. Der Graph steigt immer stärker an. Es handelt sich hierbei folglich um exponentielle Zunahme.
| Woche | Wasserfläche in |
|---|---|
| Woche | Algenfläche in |
|---|---|
b)
Der gesamte Baggersee ist genau ab dem Zeitpunkt mit Algen überdeckt, an dem die Fläche des Algenteppichs gleich groß wie die Wasserfläche ist.
Dieser Zeitpunkt entspricht dem Schnittpunkt der beiden Graphen. Aus den Graphen aus Aufgabe a) kann der Schnittpunkt an der Stelle 
abgelesen werden.
Ebenso ergibt sich durch Vergleichen der Tabellenwerte, dass die Algenfläche ab der 7. Woche größer als die Wasserfläche ist.
Im Laufe der 7. Woche bedecken die Algen folglich die gesamte Wasserfläche.
c)
Da es sich bei der Zunahme der Wasserfläche um lineare Zunahme mit dem Zunahmebetrag 150 handelt, folgt:
Da es sich bei der Zunahme der Algenfläche um exponentielle Zunahme mit dem Zunahmefaktor 3 handelt, folgt:
