Klassenbildung von Daten
Bei umfangreichen Stichproben mit zahlreichen Werten empfiehlt es sich, benachbarte Werte in Klassen zusammenzufassen.
Zur grafischen Darstellung werden Diagramme gezeichnet, wobei die Häufigkeiten als Säulen über die Klassen eingetragen werden. Fällt ein Ergebnis auf eine Klassengrenze, wird es in der Regel in die obere Klasse eingeteilt.
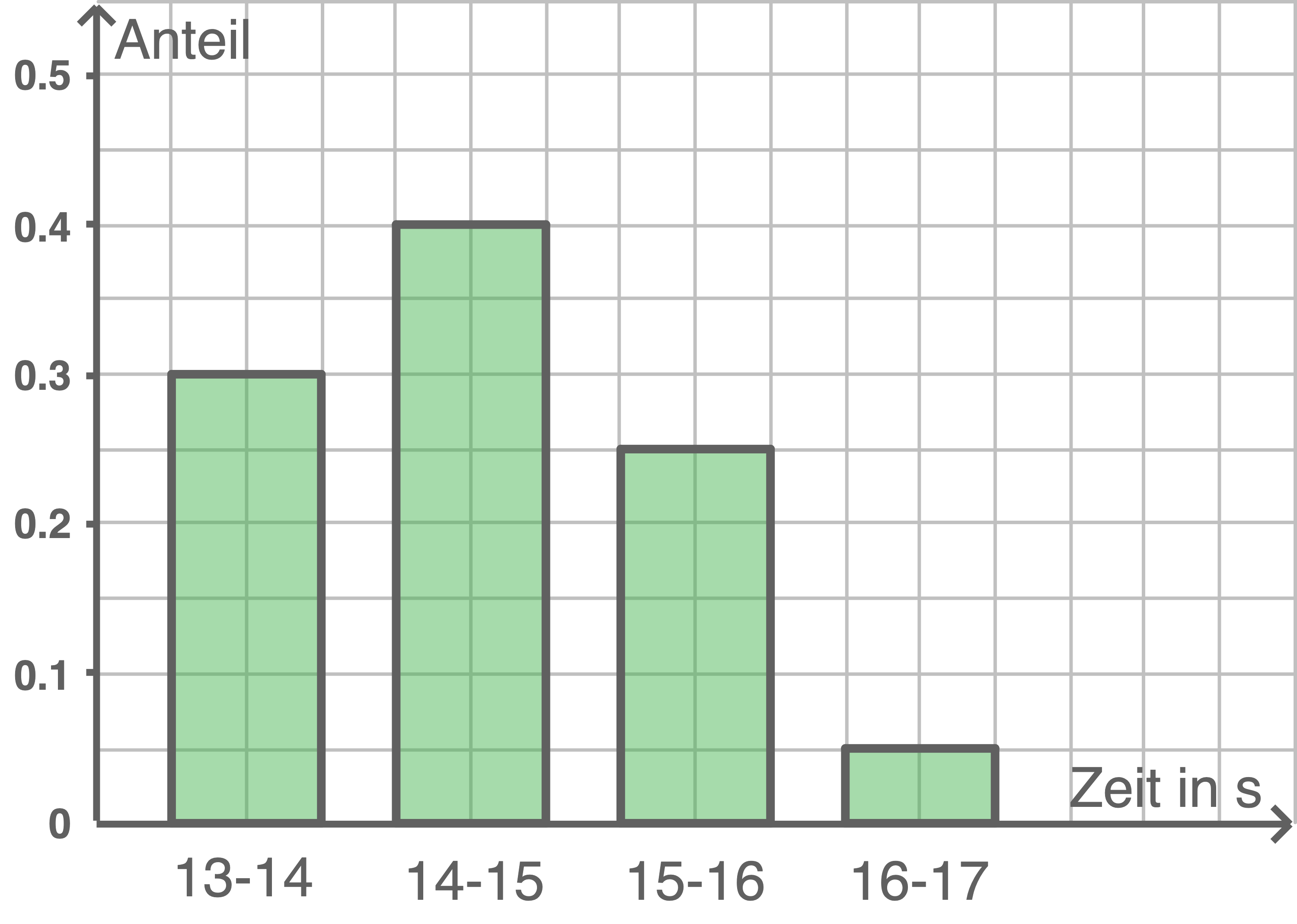
Beispiel
Zeiten einer Schulklasse bei einem 100 m-Sprint:
| 13,2 s | 14,7 s | 13,9 s | 15,3 s | 14,9 s |
| 14,3 s | 15,0 s | 14,1 s | 15,5 s | 13,1 s |
| 14,8 s | 14,3 s | 13,6 s | 16,4 s | 14,3 s |
| 13,9 s | 15,4 s | 14,2 s | 13,7 s | 15,9 s |
1
In einer Schulklasse wurden die erreichten Höhen beim Hochsprung gemessen und notiert:
| 1,23 m | 1,37 m | 1,16 m | 1,49 m | 1,05 m |
| 1,30 m | 1,05 m | 1,11 m | 1,39 m | 1,09 m |
| 1,43 m | 1,27 m | 1,33 m | 1,20 m | 1,36 m |
| 1,19 m | 1,39 m | 1,22 m | 1,27 m | 1,12 m |
a)
Erkläre, weshalb die Darstellung in einem Säulendiagramm ohne Klassierung der Daten nicht vorteilhaft wäre.
b)
Teile die Werte in fünf Klassen mit je 
ein und zeichne das zugehörige Diagramm mit relativen Häufigkeiten.
2
Bei einer Marktforschung wird das Gewicht von Kartoffeln verglichen. Die Ergebnisse sind im folgenden Diagramm dargestellt.
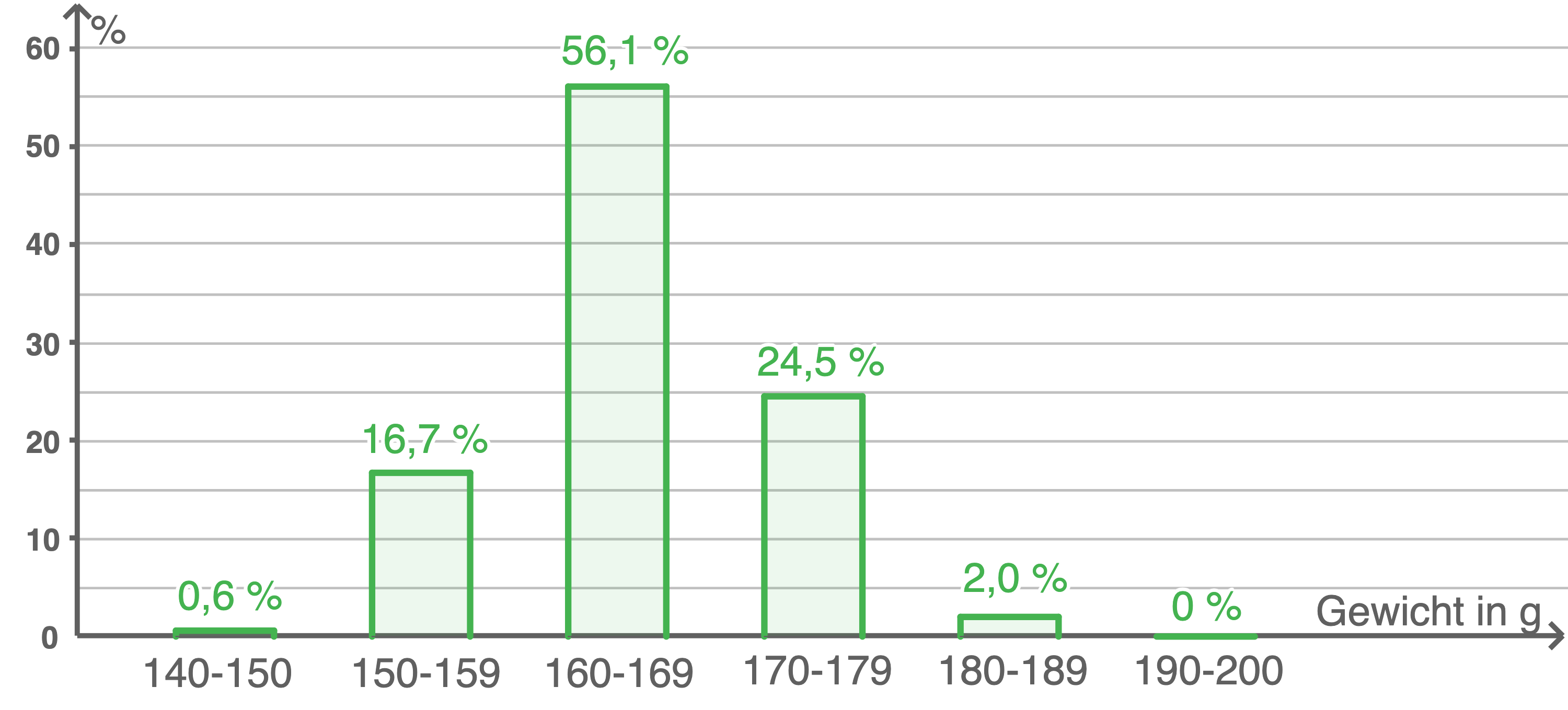Beantworte die folgenden Fragen. Begründe gegebenenfalls, warum keine Aussage getroffen werden kann.
a)
Wie viel Prozent der Kartoffeln wiegen 
b)
Wie viel Prozent der Kartoffeln wiegen weniger als 
c)
Wie viel Prozent der Kartoffeln wiegen 
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Würde man die Daten einzeln in einem Säulendiagramm darstellen, müsste man 20 Säulen einzeichnen. Das Diagramm wird dann schnell unübersichtlich.
b)
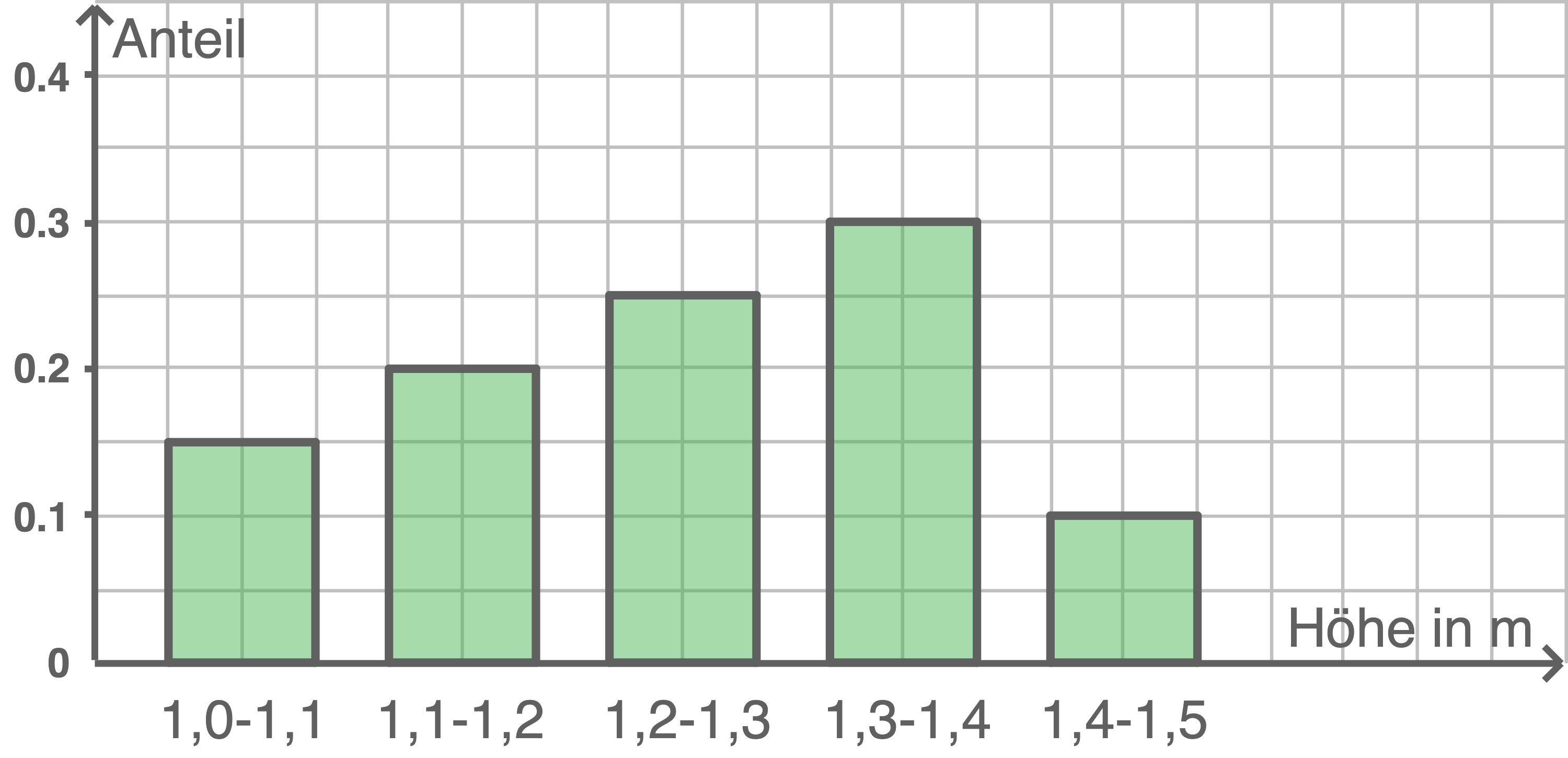
2
a)
b)
c)
Darüber kann keine Aussage getroffen werden, da über die Verteilung innerhalb der Klassen nichts bekannt ist. Das gesuchte Gewicht erstreckt sich jedoch über Abschnitte von zwei verschiedenen Klassen.