Zufallsversuche und Wahrscheinlichkeiten
Definition
Bei einem Zufallsversuch sind die möglichen Ergebnisse bekannt. Es kann jedoch nicht vorhergesagt werden, welches Ergebnis eintritt.Ein Zufallsversuch lässt sich beliebig oft wiederholen.
Beispiel
Werfen eines Würfels
In der Ergebnismenge  werden alle möglichen Ergebnisse eines Zufallsversuchs zusammengefasst.
werden alle möglichen Ergebnisse eines Zufallsversuchs zusammengefasst.
Mögliche Ergebnisse:

Ergebnisse können zu einem Ereignis  zusammengefasst werden. Die Ergebnisse, die einem Ereignis entsprechen, heißen dann günstige Ergebnisse.
zusammengefasst werden. Die Ergebnisse, die einem Ereignis entsprechen, heißen dann günstige Ergebnisse.
Ereignis  Augenzahl größer als
Augenzahl größer als 
Günstige Ergebnisse:

Günstige Ergebnisse:
Bei einem Laplace-Versuch haben alle Ergebnisse die gleiche Wahrscheinlichkeit. Die Wahrscheinlichkeit eines Ereignisses  lässt sich wie folgt berechnen:
lässt sich wie folgt berechnen:

Ereignis  Augenzahl ist gerade
Augenzahl ist gerade
mögliche Ergebnisse:
günstige Ergebnisse:

mögliche Ergebnisse:
günstige Ergebnisse:
Wird ein Zufallsversuch sehr oft wiederholt, so gilt näherungsweise:
relative Häufigkeit Wahrscheinlichkeit
Wahrscheinlichkeit
relative Häufigkeit
Wird der Würfel sehr oft geworfen, so wird etwa in einem Sechstel aller Fälle die Zahl
Die Summenregel besagt, dass die Wahrscheinlichkeit eines Ereignisses die Summe der Wahrscheinlichkeiten der zugehörigen Ergebnisse ist.
In manchen Fällen kann es einfacher sein, die Wahrscheinlichkeit eines Ereignisses  mit dem Gegenereignis
mit dem Gegenereignis  (nicht
(nicht  ) zu berechnen.
Es gilt:
) zu berechnen.
Es gilt: 
Ereignis  Zahl größer
Zahl größer 
Gegenereignis Zahl
Zahl 
![\(\begin{array}[t]{rll}
P(E)&=& 1-P(\overline{E}) \\[5pt]
&=& 1-\frac{1}{6} \\[5pt]
&=& \frac{5}{6}
\end{array}\)](https://www.schullv.de/resources/formulas/f6ae894e8335ded224ed299a2d114d33aaba57172dd00e6fed58854204f1ff0d_light.svg)
Gegenereignis
Glücksrad
Beim Glücksrad wird die Wahrscheinlichkeit durch den Anteil des Kreisausschnitts am gesamten Kreis bestimmt.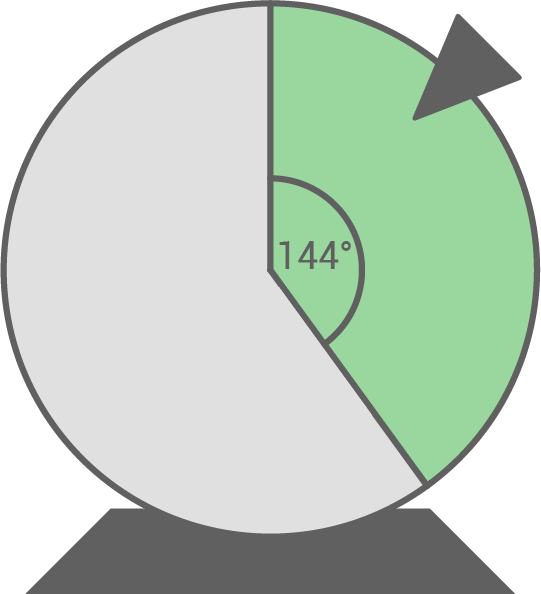
1
In einem Kaugummiautomat sind 12 orangene, 27 blaue und 21 grüne Kaugummis. Der Automat gibt zufällig ein Kaugummi aus.
a)
Wie hoch ist die Wahrscheinlichkeit, dass das Kaugummi
1)
orange ist?
2)
nicht grün ist?
3)
orange oder grün ist?
b)
Zeichne ein Glücksrad mit den Wahrscheinlichkeiten für die verschiedenen Farben.
2
In einem Gefäß sind  weiße Kugeln und weitere schwarze Kugeln. Die Wahrscheinlichkeit dafür, zufällig eine weiße Kugel zu ziehen, beträgt
weiße Kugeln und weitere schwarze Kugeln. Die Wahrscheinlichkeit dafür, zufällig eine weiße Kugel zu ziehen, beträgt 
a)
Wie viele Kugeln sind im Gefäß?
b)
Wie viele schwarze Kugeln sind im Gefäß?
c)
Mit welcher Wahrscheinlichkeit wird zufällig eine schwarze Kugel gezogen?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
2
a)
Die Anzahl  an Kugeln im Gefäß kann wie folgt berechnet werden:
an Kugeln im Gefäß kann wie folgt berechnet werden:
![\(\begin{array}[t]{rll}
n\cdot \dfrac{1}{3}&=& 10 \quad \scriptsize \mid\; \cdot 3 \\[5pt]
n&=& 30
\end{array}\)](https://www.schullv.de/resources/formulas/c3ed07b0e8fca042c75b341d9de7c308d1995399e515e893fa8bad9cd4e67815_light.svg) Im Gefäß sind insgesamt 30 Kugeln.
Im Gefäß sind insgesamt 30 Kugeln.
b)
c)