A1 – Ganzrationale Funktion
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) Gegeben ist die Funktion mit
mit  ;
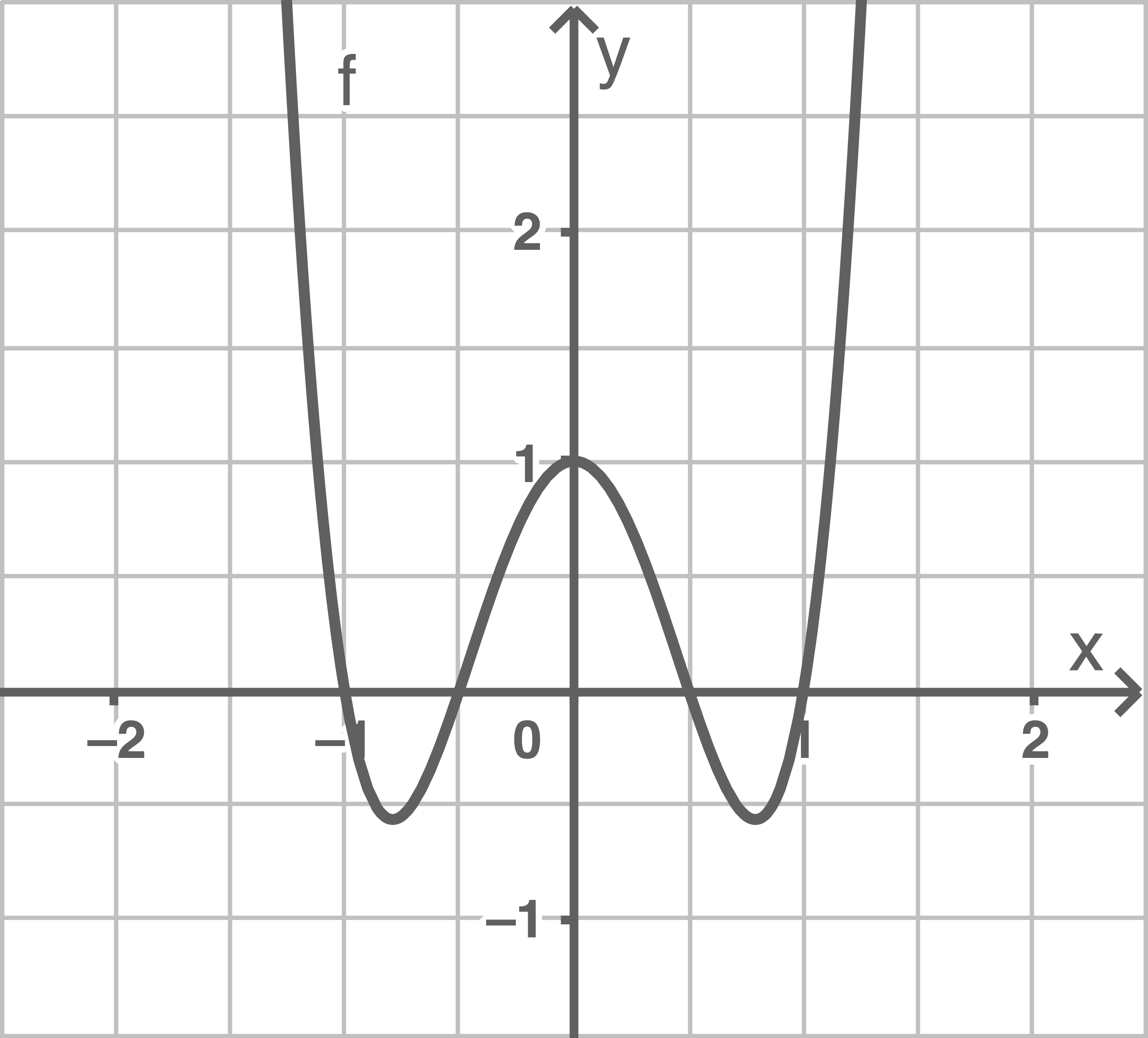
;  deren Graph
deren Graph  ist.
ist.
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) Gegeben ist die Funktion

a)
Bestimme die Schnittpunkte von  mit den Koordinatenachsen und begründe, warum der Graph symmetrisch zur y-Achse ist.
mit den Koordinatenachsen und begründe, warum der Graph symmetrisch zur y-Achse ist.
b)
Berechne die Koordinaten der Tiefpunkte und gib die Gleichung der Tangente im Hochpunkt an.
c)
Beschreibe, wie man die Gleichung der Tangente im Punkt  aufstellt und wie man die entsprechende Gleichung der Tangente im Punkt
aufstellt und wie man die entsprechende Gleichung der Tangente im Punkt  erhält.
erhält.
d)
Die Tangente an  im Punkt
im Punkt  bildet zusammen mit den Koordinatenachsen ein Dreieck. Beschreibe, wie man den Flächeninhalt dieses Dreiecks berechnen kann.
bildet zusammen mit den Koordinatenachsen ein Dreieck. Beschreibe, wie man den Flächeninhalt dieses Dreiecks berechnen kann.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Die Schnittpunkte lassen sich ablesen. Die Schnittpunkte mit der  -Achse sind
-Achse sind 

 und
und  Der Schnittpunkt mit der
Der Schnittpunkt mit der  -Achse lautet
-Achse lautet  Der Graph ist symmetrisch zur
Der Graph ist symmetrisch zur  -Achse, da die Funktion
-Achse, da die Funktion  lediglich gerade Exponenten aufweist.
lediglich gerade Exponenten aufweist.
b)
Koordinaten der Tiefpunkte berechnen
1. Schritt: Ableitungen bilden

 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/1c987ac85704cf743cd6bf75999b1ca49c216622bb238f7557f6e7fb725edd6e_light.svg) Mit dem Satz vom Nullprodukt ergeben sich
Mit dem Satz vom Nullprodukt ergeben sich  und
und
![\(\begin{array}[t]{rll}
8x^2-5&=& 0&\quad \scriptsize \mid\;+5 \mid \; :8 \\[5pt]
x^2&=&\dfrac{5}{8} &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
x_{2 /3}&=& \pm \sqrt{\frac{5}{8}}
\end{array}\)](https://www.schullv.de/resources/formulas/f90e1dcc9e7703061c686a392364d3058fffae88efa9987442fc96499e453f10_light.svg) Mögliche Extremstellen sind also
Mögliche Extremstellen sind also 
 und
und  3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/39900e151552cea5d9bb64efba256bd37bd74a71be11773f1c8530327eef7202_light.svg) Da
Da  liegt an der Stelle
liegt an der Stelle  ein Minimum vor.
Wegen der Symmetrie zur
ein Minimum vor.
Wegen der Symmetrie zur  -Achse und mit Hilfe der Abbildung kann darauf geschlossen werden, dass an der Stelle
-Achse und mit Hilfe der Abbildung kann darauf geschlossen werden, dass an der Stelle  ebenfalls ein Minimum vorliegt.
ebenfalls ein Minimum vorliegt.
![\(\begin{array}[t]{rll}
f\left(\sqrt{\frac{5}{8}} \right)&=&4\cdot \left(\sqrt{\frac{5}{8}} \right)^4-5\cdot \left(\sqrt{\frac{5}{8}} \right)^2+1 \\[5pt]
&=&\dfrac{4 \cdot 5^2}{8^2}- \dfrac{5\cdot 5}{8}+1 \\[5pt]
&=&\dfrac{25}{16}- \dfrac{25}{8}+1 \\[5pt]
&=& \dfrac{25}{16}- \dfrac{50}{16}+\dfrac{16}{16} \\[5pt]
&=& -\dfrac{9}{16}
\end{array}\)](https://www.schullv.de/resources/formulas/91ed896bd5245dd0c6a377f5f4c720dcde9c36630a7373d139d1dd13899537b0_light.svg) Wegen der Achsensymmetrie gilt ebenfalls
Wegen der Achsensymmetrie gilt ebenfalls  Somit folgen die Koordinaten der Tiefpunkte mit
Somit folgen die Koordinaten der Tiefpunkte mit  und
und  Gleichung der Tangente im Hochpunkt angeben
Die Stelle
Gleichung der Tangente im Hochpunkt angeben
Die Stelle  entspricht einem Maximum, da sie zwischen den beiden Tiefpunkten liegt.
Die Steigung einer Tangente im Hochpunkt beträgt
entspricht einem Maximum, da sie zwischen den beiden Tiefpunkten liegt.
Die Steigung einer Tangente im Hochpunkt beträgt  Der
Der  -Achsenabschnitt von
-Achsenabschnitt von  ergibt sich zu
ergibt sich zu  Daher lautet die Gleichung der Tangente
Daher lautet die Gleichung der Tangente 
c)
- Aufstellen der ersten Ableitungsfunktion
- Berechnung der Steigung durch Einsetzen von
in die erste Ableitungsfunktion
- Allgemeine Geradengleichung
- Einsetzen von
sowie der Steigung ergibt die Tangentengleichung
d)
- Tangentengleichung aufstellen
- Schnittpunkte
und
der Tangente mit den Koordinatenachsen bestimmen
- Es handelt sich um ein rechtwinkliges Dreieck mit
entspricht der
-Koordinate von
der
-Koordinate von
da das Dreieck im ersten Quadranten liegt.