AG3 – Quadratische Pyramide
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) Die Punkte ,
,  und
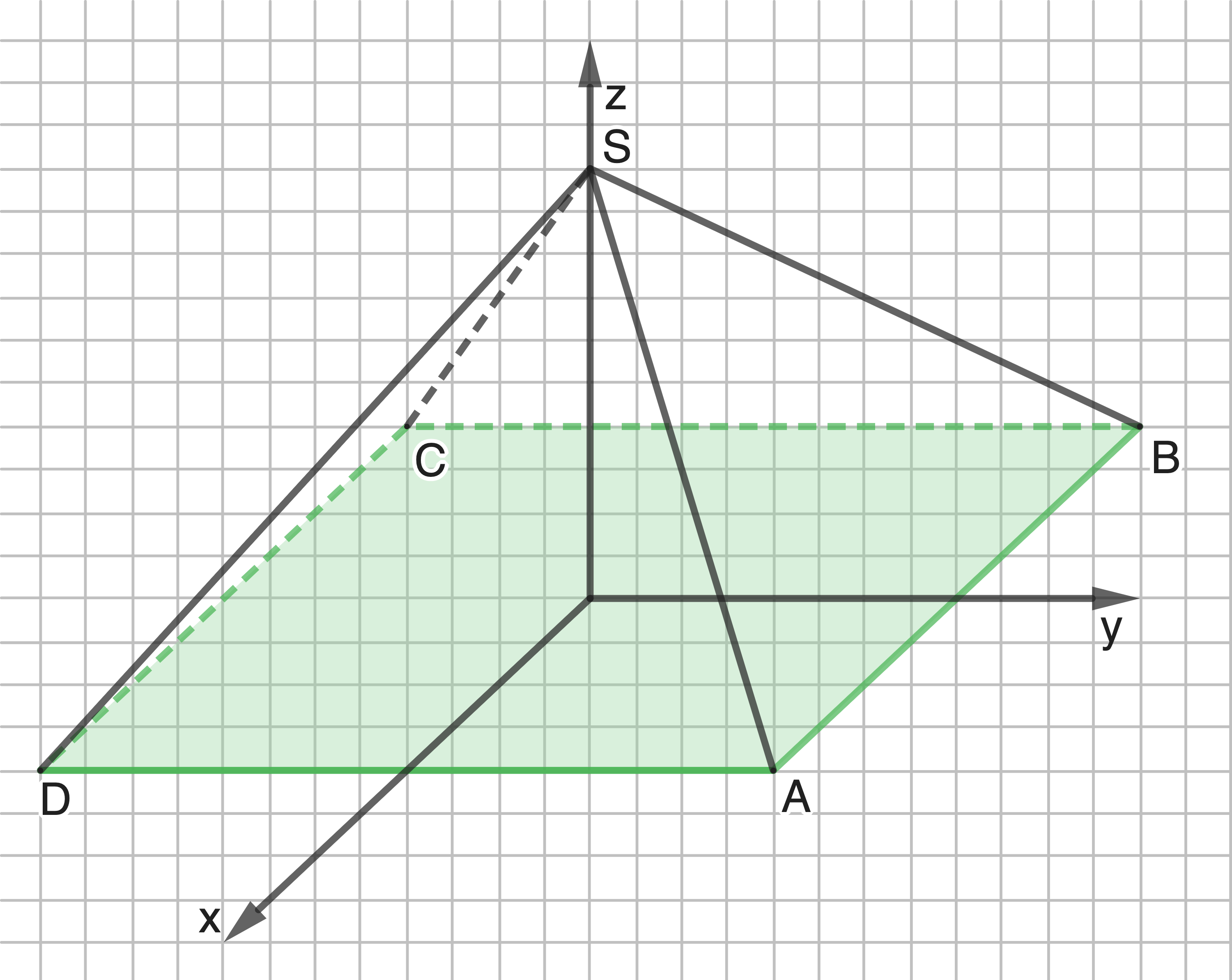
und  sind Eckpunkte einer quadratischen senkrechten Pyramide
sind Eckpunkte einer quadratischen senkrechten Pyramide  , deren Grundfläche
, deren Grundfläche  in der
in der  -Ebene liegt.
-Ebene liegt.
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) Die Punkte

a)
Bestimme die Koordinaten der Eckpunkte  und
und  und gib die Gleichung der Ebene
und gib die Gleichung der Ebene  in Parameterform an, in der die Punkte
in Parameterform an, in der die Punkte  ,
,  und
und  liegen.
liegen.
b)
Zeige, dass das Dreieck  gleichschenklig ist.
gleichschenklig ist.
c)
Beschreibe, wie man die Oberfläche der Pyramide berechnen kann.
d)
Die Ebene  mit
mit  soll senkrecht zur Ebene
soll senkrecht zur Ebene  sein. Bestimmt
sein. Bestimmt  so, dass
so, dass  und
und  senkrecht zueinander liegen.
senkrecht zueinander liegen.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Ablesen ergibt  sowie
sowie 


b)
Die Punkte  und
und  liegen in der
liegen in der  -Ebene. Die Punkte
-Ebene. Die Punkte  und
und  haben jeweils den gleichen Abstand zur
haben jeweils den gleichen Abstand zur  -Achse. Da der Punkt
-Achse. Da der Punkt  in der
in der  -Ebene liegt, muss das Dreieck
-Ebene liegt, muss das Dreieck  gleichschenklig sein.
gleichschenklig sein.
c)
Die Oberfläche besteht aus der Grundfläche  und aus vier gleichschenkligen Dreiecken, die alle den gleichen Flächeninhalt haben wie z.B. das Dreieck
und aus vier gleichschenkligen Dreiecken, die alle den gleichen Flächeninhalt haben wie z.B. das Dreieck  Der Inhalt der Grundfläche lässt sich berechnen, indem die beiden Längen der Strecken
Der Inhalt der Grundfläche lässt sich berechnen, indem die beiden Längen der Strecken  und
und  miteinander multipliziert werden.
Der Flächeninhalt des Dreiecks
miteinander multipliziert werden.
Der Flächeninhalt des Dreiecks  lässt sich berechnen, indem die Länge der Strecke
lässt sich berechnen, indem die Länge der Strecke  mit der Länge der Strecke
mit der Länge der Strecke  sowie dem Faktor
sowie dem Faktor  multipliziert wird, wobei
multipliziert wird, wobei  der Mittelpunkt der Strecke
der Mittelpunkt der Strecke  ist.
ist.
d)
Aufstellen des Normalenvektors der Ebene  durch Bildung des Kreuzprodukts der beiden Richtungsvektoren:
durch Bildung des Kreuzprodukts der beiden Richtungsvektoren:




 Der Normalenvektor der Ebene
Der Normalenvektor der Ebene  lässt sich ablesen:
lässt sich ablesen:
 Damit die beiden Vektoren senkrecht zueinander liegen, muss deren Skalarprodukt gleich Null sein.
Damit die beiden Vektoren senkrecht zueinander liegen, muss deren Skalarprodukt gleich Null sein.



