A8 – Tesla

Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Taschenrechner (WTR)

Die Produktion eines Teslamodells wird modelliert. Die momentane Produktionsrate wird durch die Funktion $f$ mit $f(t)=1000t\cdot \mathrm e^{-0,5t}$ für $0\leq t \leq 12$ beschrieben.
Ihr Graph ist $K.$

$(t$ in Monaten nach Produktionsbeginn, $f(t)$ in Autos pro Monat)

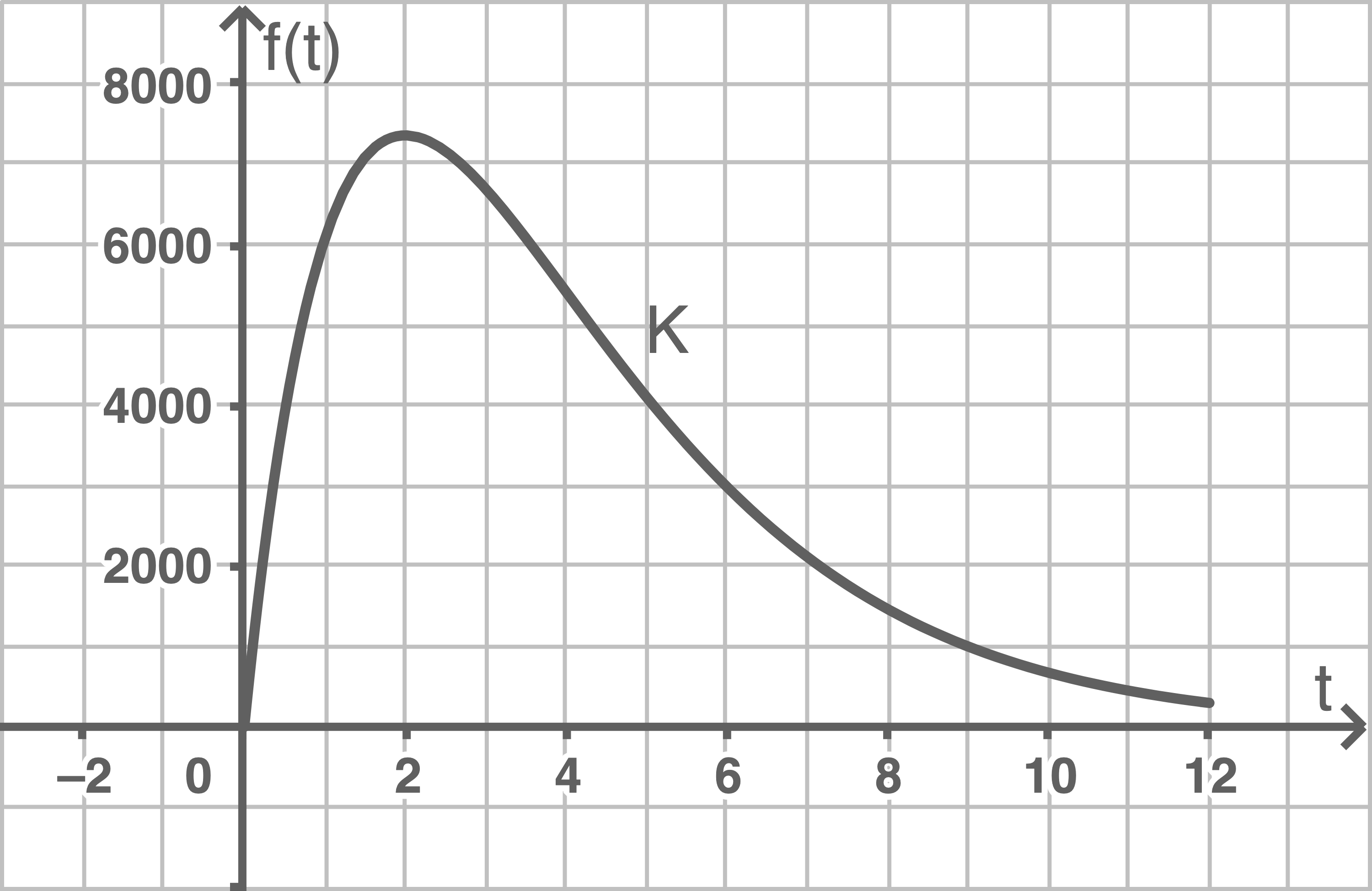
Grafik eines Funktionsverlaufs mit Achsenbeschriftungen für f(t) und t.

Gib die maximale momentane Produktionsrate an.

Bestimme anhand der Abbildung den Zeitraum, zu dem die Produktionsrate mehr als 400 Autos pro Monat beträgt.

Wann nimmt die momentane Produktionsrate am stärksten ab bzw. zu? Bestimme die Zeitpunkte anhand der Abbildung näherungsweise.

Erkläre, wie die Gesamtanzahl der produzierten Autos 4 Monate nach Produktionsbeginn bestimmt werden kann. Gib einen Term an und bestimme den Wert des Terms näherungsweise.

Überprüfe: $\displaystyle\int_{t}^{t+1}f(t)\;\mathrm dt=2000$ und überlege dir eine Fragestellung im Sachzusammenhang.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Das Maximum kann aus $K$ abgelesen werden, nämlich zum Zeitpunkt $t \approx 2$ mit $f(2) \approx 7400.$

Die maximale momentane Änderungsrate entspricht ca. 7400 Autos pro Monat.

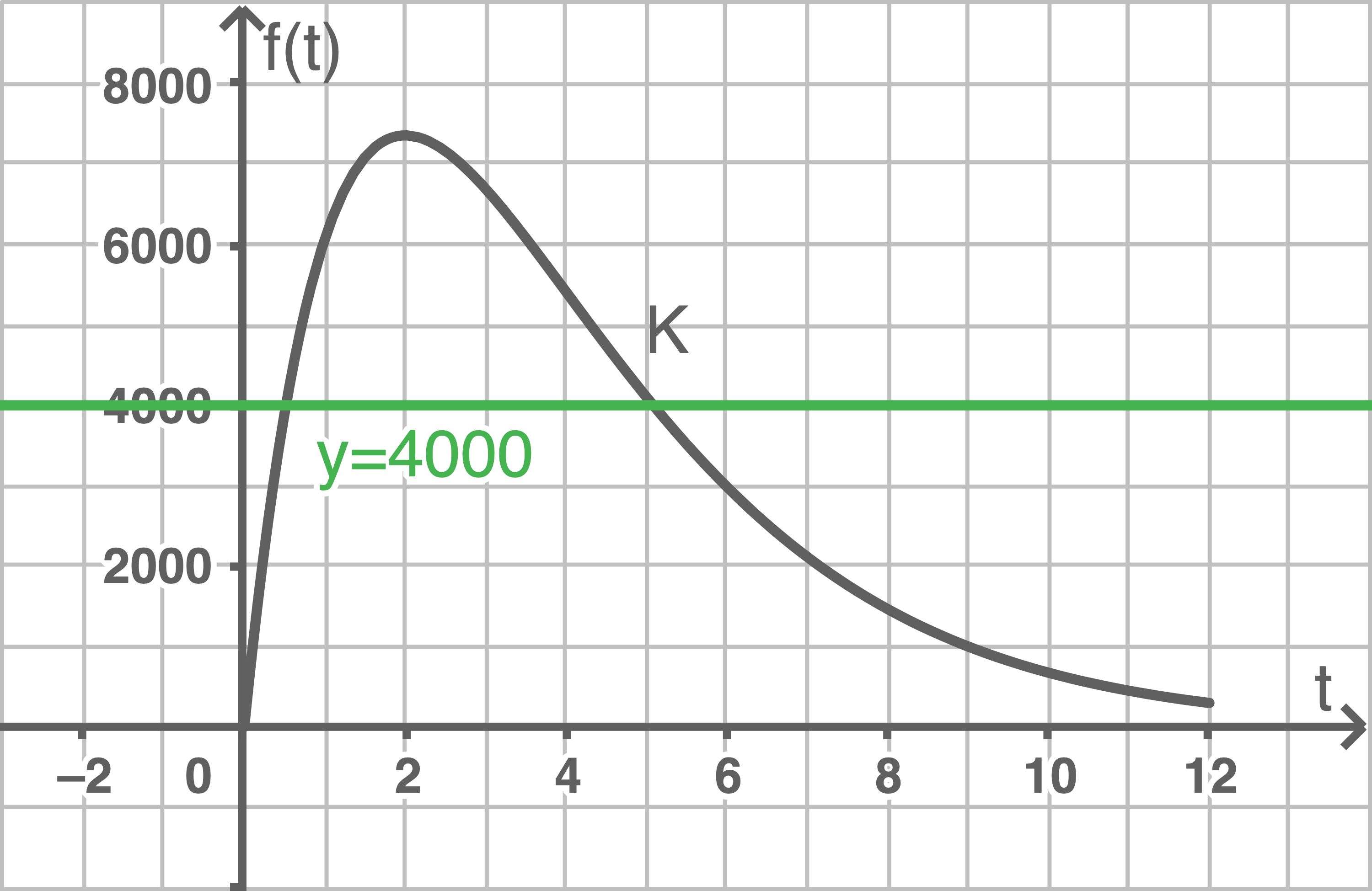
aufgabe 8 basisfach bw abi änderungsrate auto

Die Gerade zu $y=4000$ wird in die Abbildung eingezeichnet. Die Schnittstellen mit $K$ sind $t_1 \approx 0,5$ und $t_2 \approx 5.$

Im Zeitraum von einem halben Monat bis 5 Monate nach Produktionsbeginn werden mehr als 4000 Autos pro Monat produziert.

Die stärkste Zu- bzw. Abnahme der Produktionsrate entspricht den Stellen mit maximaler bzw. minimaler Tangentensteigung. Diese liegen an den Stellen $t \approx 0,$ also zu Produktionsbeginn, und an $t\approx 4$ an der Wendestelle.
An der Stelle $t=0$ steigt $K,$ also nimmt die Produktionsrate zu Beginn zu.
Nach dem Hochpunkt fällt $K$ und damit nimmt die Produktionsrate ab.

Die Produktionsrate nimmt zu Produktionsbeginn am stärksten zu und vier Monate nach Produktionsbeginn am stärksten ab.

Die Gesamtanzahl der produzierten Autos vier Monate nach Produktionsbeginn wird mithilfe eines Integrals bestimmt.

Es gilt: $\displaystyle\int_{0}^{4}f(t)\;\mathrm dt$

Der Wert dieses Integrals entspricht dem Inhalt der Fläche, die $K$ mit der $x$ -Achse im Intervall $[0;4]$ einschließt und kann näherungsweise durch Kästchen zählen bestimmt werden.
Es sind ca. 24 Kästchen.

$\displaystyle\int_{0}^{4}f(t)\;\mathrm dt \approx 24 \cdot 1\cdot 1000 = 24000$

In den ersten vier Monaten werden ungefähr 24000 Autos produziert.

An den Integralgrenzen $t$ und $t+1$ ist erkennbar, dass es sich um einen Zeitraum von einem Monat handelt. Folglich wird das Zeitintervall $[t;t+1]$ gesucht, in dem der Inhalt der Fläche, den $K$ mit der $x$ -Achse einschließt, den Wert 2000 hat. Das entspricht also ca. zwei ganzen Kästchen in der Abbildung.
Im Intervall $[6,5;7,5]$ ist dies ungefähr der Fall.

Fragestellung im Sachzusammenhang
„In welchem Einmonatszeitraum werden 2000 neue Autos produziert?“

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?