S7 – Zufallsexperiment
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) In einem Gefäß befinden sich Kugeln, die mit Zahlen beschriftet sind: Zwei Kugeln mit einer 3 und vier Kugeln mit einer 6.
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) In einem Gefäß befinden sich Kugeln, die mit Zahlen beschriftet sind: Zwei Kugeln mit einer 3 und vier Kugeln mit einer 6.
a)
Drei Kugeln werden mit Zurücklegen gezogen. Berechne die Wahrscheinlichkeiten für die folgenden Ereignisse:
A: „Die Summe der Zahlen beträgt 15.“
B: „Es werden zwei gleiche Zahlen hintereinander gezogen.“
B: „Es werden zwei gleiche Zahlen hintereinander gezogen.“
b)
Jetzt werden 50 Kugeln mit Zurücklegen gezogen. Gib einen Term für die Wahrscheinlichkeit an, dass genau neun Kugeln mit der Zahl 6 gezogen werden. Erkläre die Vorgehensweise.
Die Kugeln, die mit den Zahlen 3 beschriftet sind, werden ersetzt durch eine andere von 6 verschiedene Zahl
c)
Welche Wahrscheinlichkeit wird mit 
berechnet? Beschreibe ein Ereignis im Sachzusammenhang.
d)
Überprüfe: „Werden zwei Kugeln nacheinander und ohne Zurücklegen gezogen, so entspricht der Erwartungswert der Summe der Zahlen 28.“
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Um drei Kugeln zu ziehen, die die Augensumme 15 ergeben, müssen zwei Kugeln mit einer 6 und eine Kugel mit einer 3 gezogen werden. Die Wahrscheinlichkeit ergibt sich mit den Pfadregeln:
b)
Es werden 50 Kugeln mit Zurücklegen gezogen. Bei jedem Zug kann entweder eine Kugel mit einer 3 oder eine Kugel mit einer 6 gezogen werden. Ein möglicher Term ergibt sich folglich mithilfe der Binomialverteilung. Die Zufallsvariable 
wird für die Anzahl der gozogenen Kugeln mit der Zahl 6 festgelegt. ist binomialverteilt mit den Parametern 
und 
c)
Die Wahrscheinlichkeit, eine Kugel mit der Zahl 6 zu ziehen, beträgt 
Mit 
wird die Wahrscheinlichkeit bestimmt, dreimal hintereinander eine Kugel mit der Zahl 6 zu ziehen.
Mit
ergibt sich die Wahrscheinlichkeit des Gegenereignisses.
Ein zum Term passendes Ereignis ist: „Mindestens eine Kugel mit der Zahl 
wird gezogen.“
Mit
d)
Den Erwartungswert 
für die Summe der Zahlen ergibt sich mit den Pfadregeln:
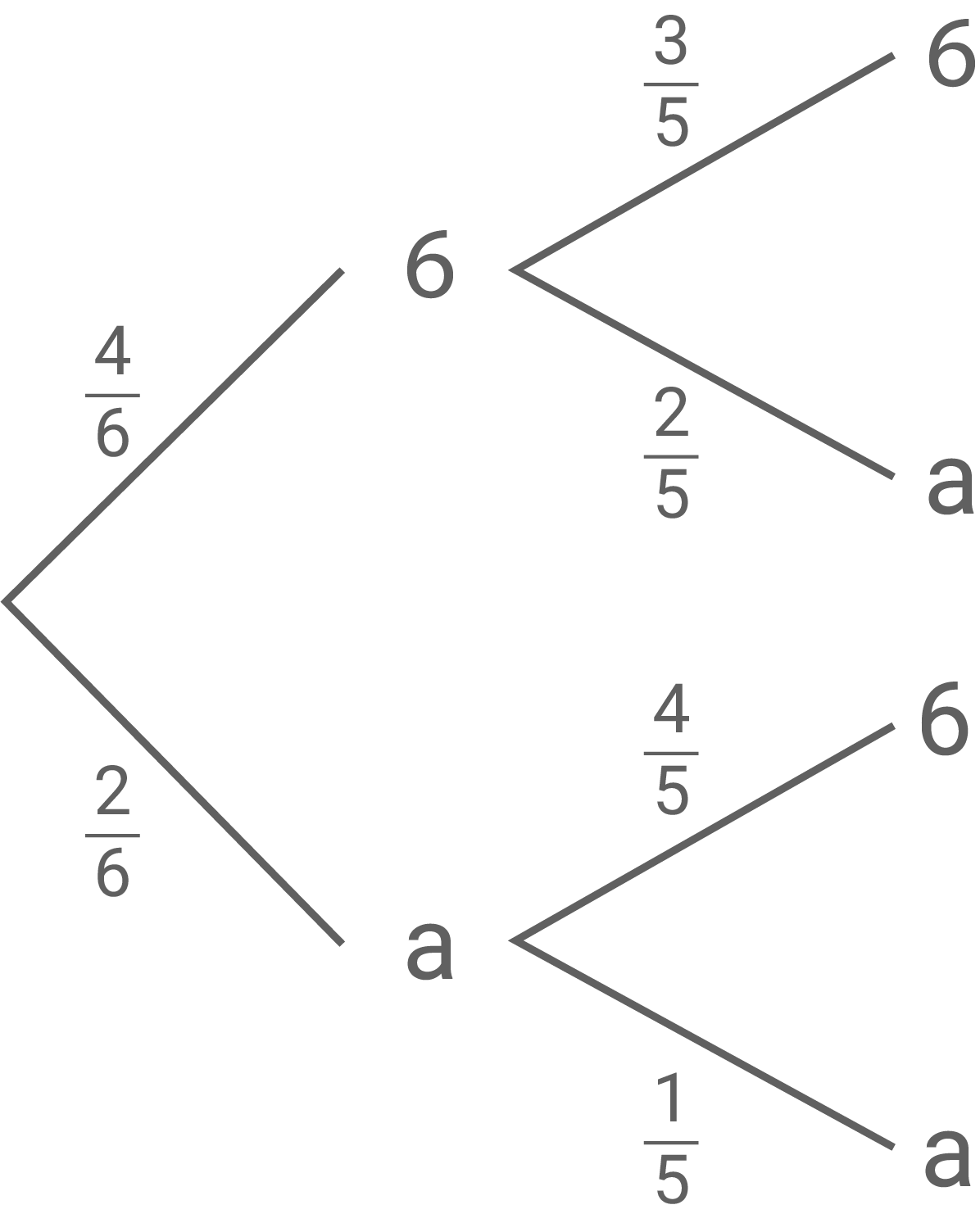
![\(\begin{array}[t]{rll}
\mu&=& \dfrac{4}{6}\cdot\dfrac{3}{5} \cdot (6+6) +\dfrac{4}{6} \cdot \dfrac{2}{5} \cdot (6+a) \\[5pt]
&+& \dfrac{2}{6} \cdot \dfrac{4}{5} \cdot (a+6) + \dfrac{2}{6} \cdot \dfrac{1}{5}\cdot (a+a) \\[5pt]
&=& \dfrac{24}{5} +\dfrac{8}{5}+\dfrac{4}{15}a + \dfrac{4}{15} \cdot a + \dfrac{8}{5}+\dfrac{2}{15}a \\[5pt]
&=&\dfrac{40}{5} + \dfrac{10}{15} \cdot a \\[5pt]
&=& 8 + \dfrac{2}{3} \cdot a
\end{array}\)](https://mathjax.schullv.de/dfe272f615b33893093e96a8000753851023c562ef5086b5e9fe64f20c41be39?color=5a5a5a)
Es soll 
gelten und daraus folgt:
![\(\begin{array}[t]{rll}
\mu&=& 28 \\[5pt]
8 + \dfrac{2}{3} \cdot a &=& 28 \quad \scriptsize \mid\;-8 \\[5pt]
\dfrac{2}{3}\cdot a&=& 20 \quad \scriptsize \mid\; \cdot \dfrac{3}{2} \\[5pt]
a &= & 30\\[5pt]
\end{array}\)](https://mathjax.schullv.de/eea6f663cc297bdbf43eb741f1b9ed034f66a524c7c08932b12b5dc2dd258ca2?color=5a5a5a)
Wenn 
ist, ist die Aussage richtig.