S3 – Zufallsexperiment
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) In einer Urne befinden sich sechs rote und vier gelbe Kugeln. Bei einem Zufallsexperiment wird eine Kugel aus der Urne mit Zurücklegen gezogen. Dies wird mehrmals nacheinander durchgeführt.
beschreibt die Anzahl der dabei gezogenen roten Kugeln.
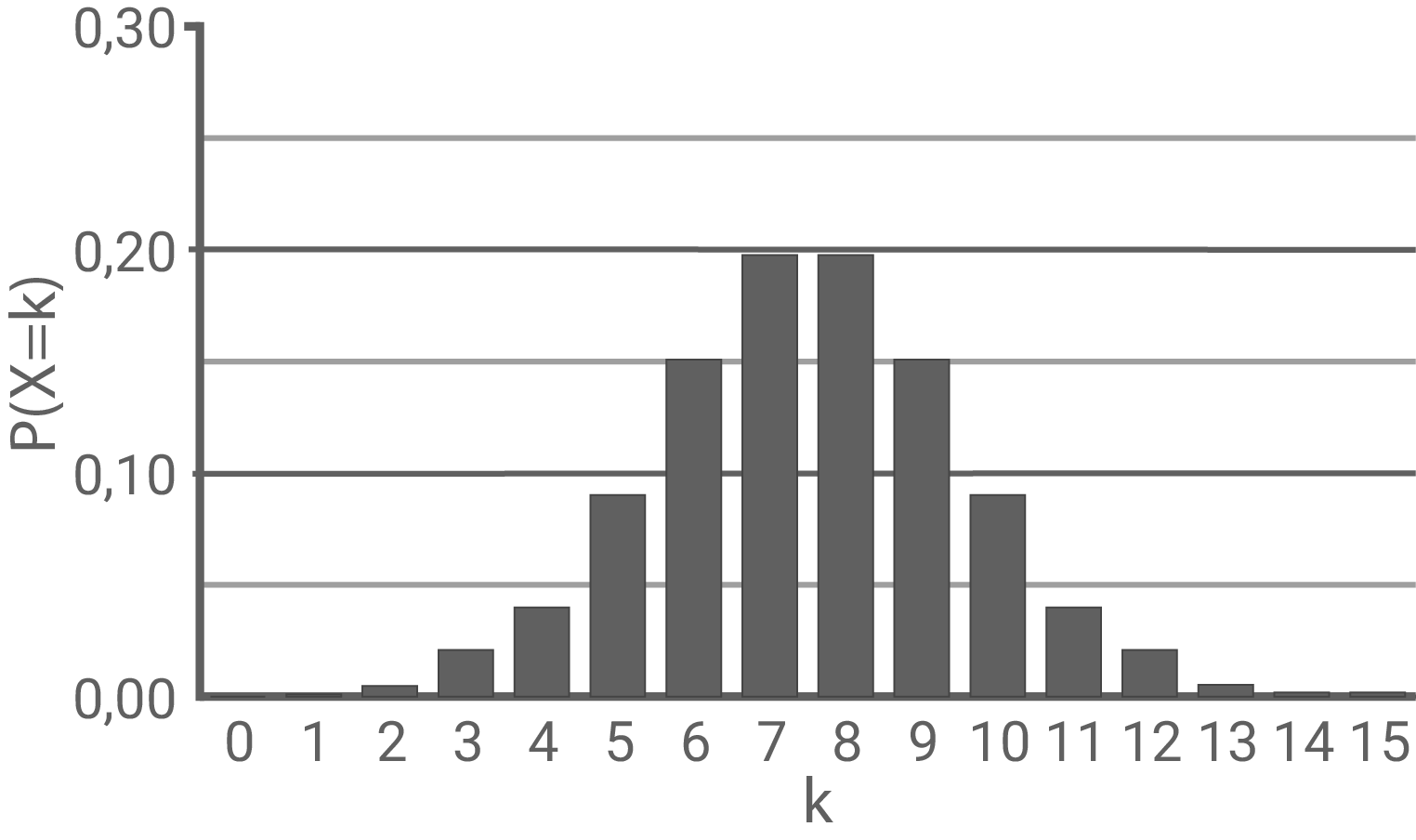
Die Abbildungen entsprechen Histogrammen, die die Binomialverteilungen von Zufallsgrößen bei 15-maliger Durchführung des Bernoulli-Experiments darstellen.
Begründe, welches der Diagramme die Verteilung von darstellt.
Untersuche die beiden anderen Diagramme hinsichtlich der Aussagen, die jeweils über die zugehörige Trefferwahrscheinlichkeit möglich sind.
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) In einer Urne befinden sich sechs rote und vier gelbe Kugeln. Bei einem Zufallsexperiment wird eine Kugel aus der Urne mit Zurücklegen gezogen. Dies wird mehrmals nacheinander durchgeführt.
a)
Das Zufallsexperiment wird dreimal nacheinander durchgeführt. Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse:
A: „Alle Kugeln sind rot.“
B: „Genau zwei der gezogenen Kugeln sind rot.“
Nun wird das Zufallsexperiment 15-mal nacheinander durchgeführt. Die Zufallsgröße A: „Alle Kugeln sind rot.“
B: „Genau zwei der gezogenen Kugeln sind rot.“
b)
Begründe, dass binomialverteilt ist.
Bestimme den Erwartungswert von und erläutere die Bedeutung im Sachzusammenhang.
„Es werden mindestens 5 und höchstens 10 rote Kugeln gezogen." Berechne die Wahrscheinlichkeit.
Bestimme den Erwartungswert von
„Es werden mindestens 5 und höchstens 10 rote Kugeln gezogen." Berechne die Wahrscheinlichkeit.
c)
Abbildung 1
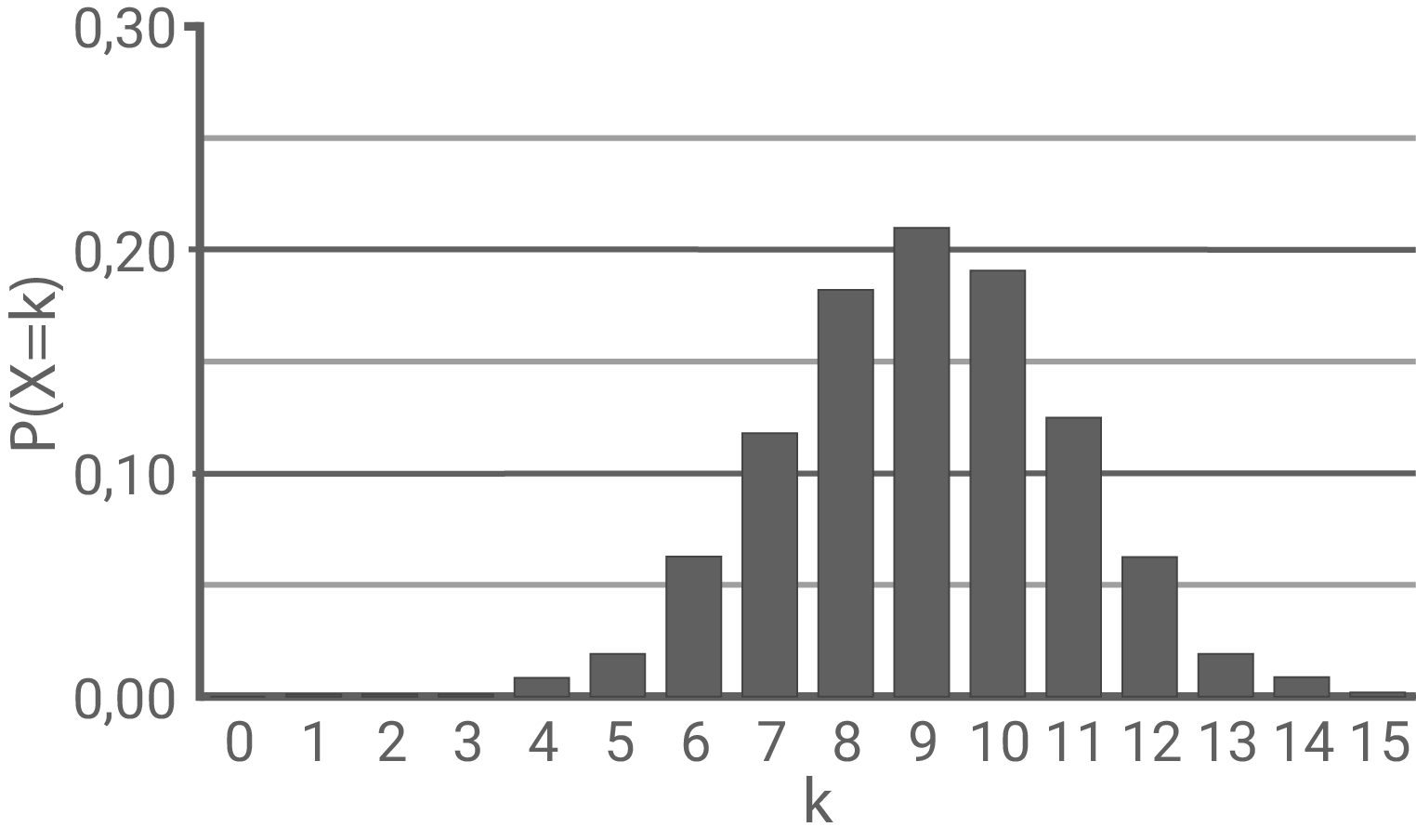
Abbildung 2
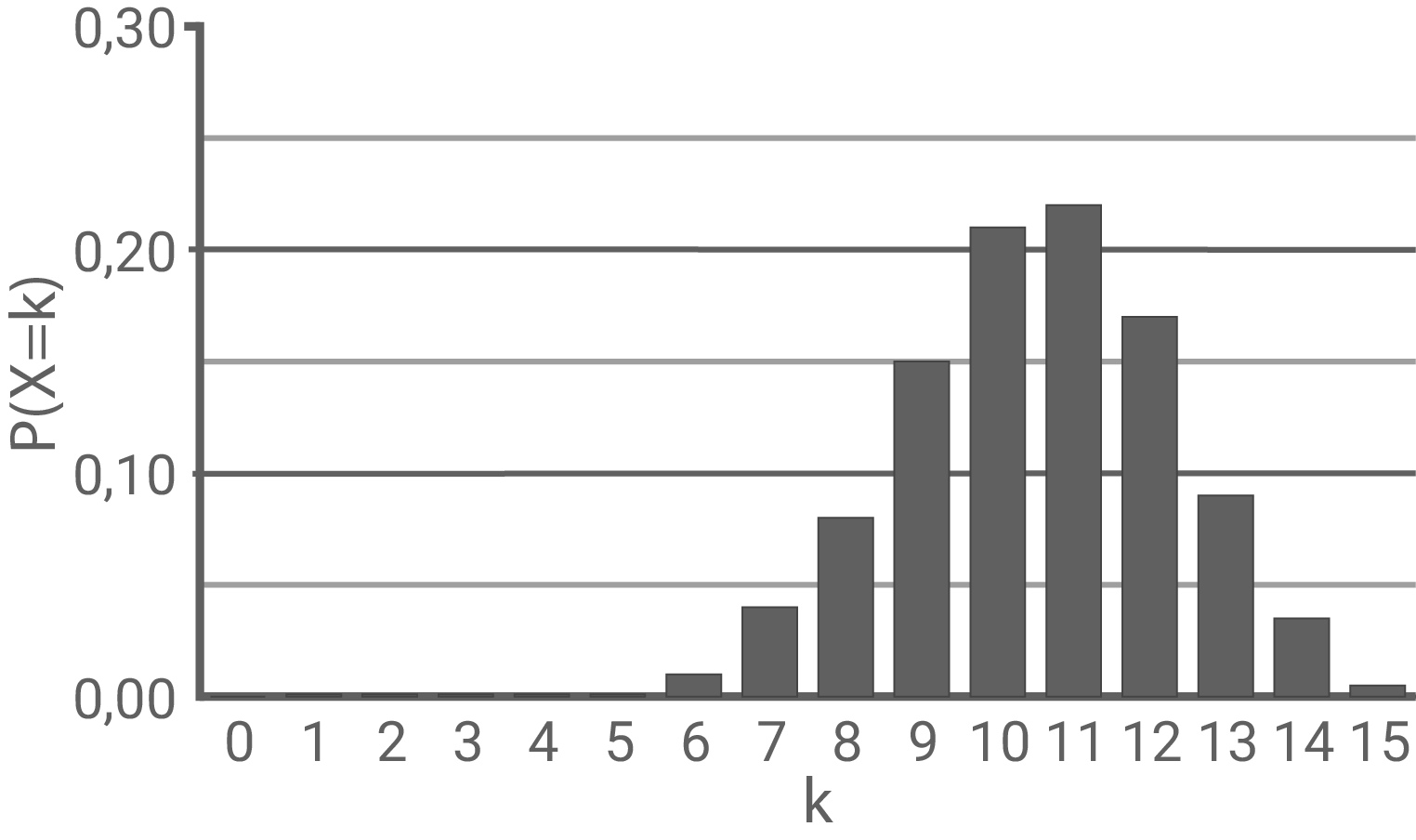
Abbildung 3
Begründe, welches der Diagramme die Verteilung von
Untersuche die beiden anderen Diagramme hinsichtlich der Aussagen, die jeweils über die zugehörige Trefferwahrscheinlichkeit möglich sind.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Die Wahrscheinlichkeit, eine rote Kugel zu ziehen, beträgt 
und die Wahrscheinlichkeit, eine gelbe Kugel zu ziehen, beträgt 
Anwenden der Pfadregeln ergibt:
b)
Binomialverteilung begründen
ist binomialverteilt, da es bei jedem Zug nur zwei mögliche Ergebnisse gibt und die Ergebnisse der 15 einzelnen Versuche wegen des Zurücklegens unabhängig voneinander sind, wodurch die Wahrscheinlichkeiten bei jedem Versuch gleich bleiben.
Erwartungswert bestimmen und deuten
Mit der Formel für den Erwartungswert einer Binomialverteilung gilt
Im Sachzusammenhang bedeutet der Erwartungswert: Wird das Zufallsexperiment häufig durchgeführt, kann davon ausgegangen werden, dass im Mittel 9 von 15 Kugeln rot sind.
Wahrscheinlichkeit berechnen
Die Wahrscheinlichkeit wird mit dem Taschenrechner bestimmt.
Mit der Formel für den Erwartungswert einer Binomialverteilung gilt
Die Wahrscheinlichkeit wird mit dem Taschenrechner bestimmt.
c)
Diagrammzuordnung begründen
Es gilt
und deshalb muss der höchste Balken des zugehörigen Diagramms bei 
liegen. Dies ist nur bei Abbildung 2 der Fall.
Trefferwahrscheinlichkeiten bestimmen
Das Diagramm in Abbildung 1 ist achsensymmetrisch, deshalb ist
Beim Diagramm in Abbildung 3 muss 
gelten. Da 
ist, folgt 
und daraus 
Es gilt
Das Diagramm in Abbildung 1 ist achsensymmetrisch, deshalb ist