S6 – Normalverteilung

Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)

Gegeben ist eine normalverteilte Zufallsgröße $X$ mit $\mu=20$ und $\sigma= 5.$

Skizziere den Graphen der zugehörigen Dichtefunktion im Intervall $[0;40].$

Normalverteilung zeichnen Stochastik BF Abi

Begründe warum $P(X\leq 20)=0,5$ gilt.

Beschreibe, wie sich die Kurve ändert, wenn $\mu$ verändert wird.

Beschreibe, wie sich die Kurve ändert, wenn $\sigma$ verändert wird.

Nenne und erläutere Gemeinsamkeiten und Unterschiede zwischen der Binomialverteilung und der Normalverteilung.

Stelle dar, wie eine diskret verteilte Zufallsgröße ermittelt werden kann, deren Histogramm eine ähnliche Form wie die Kurve aus Aufgabenteil a) hat.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die Achsen in der Abbildung werden mit $x$ und $\varphi_{20;5}(x)$ beschriftet.

Es gilt: $\varphi_{20;5}(x)=P(X=x).$

Mit dem WTR lassen sich die Wahrscheinlichkeiten für verschiedene $x$ -Werte bestimmen. Wegen der Normalverteilung handelt es sich beim Graphen um eine Glockenkurve.

Der Hochpunkt der Kurve befindet sich wegen $\mu=20$ an der Stelle $x=20.$ Die Wendepunkte der Kurve liegen an den Stellen $x_1=\mu - \sigma=20-5=15$ und $x_2=\mu +\sigma=20+5=25.$

Die $y$ -Koordinate des Hochpunktes und die $y$ -Koordinaten der Wendepunkte entsprechen den Wahrscheinlichkeiten und können mit dem WTR berechnet werden: $P(X=15) \approx 0,05,$ $P(X=20) \approx 0,08$ und wegen der Symmetrie $P(X=25) \approx 0,05.$

Die Koordinaten des Hochpunktes sind folglich $(20 \mid 0,08),$ die Koordinaten der Wendepunkte $(15\mid 0,05)$ und $(25\mid 0,05).$

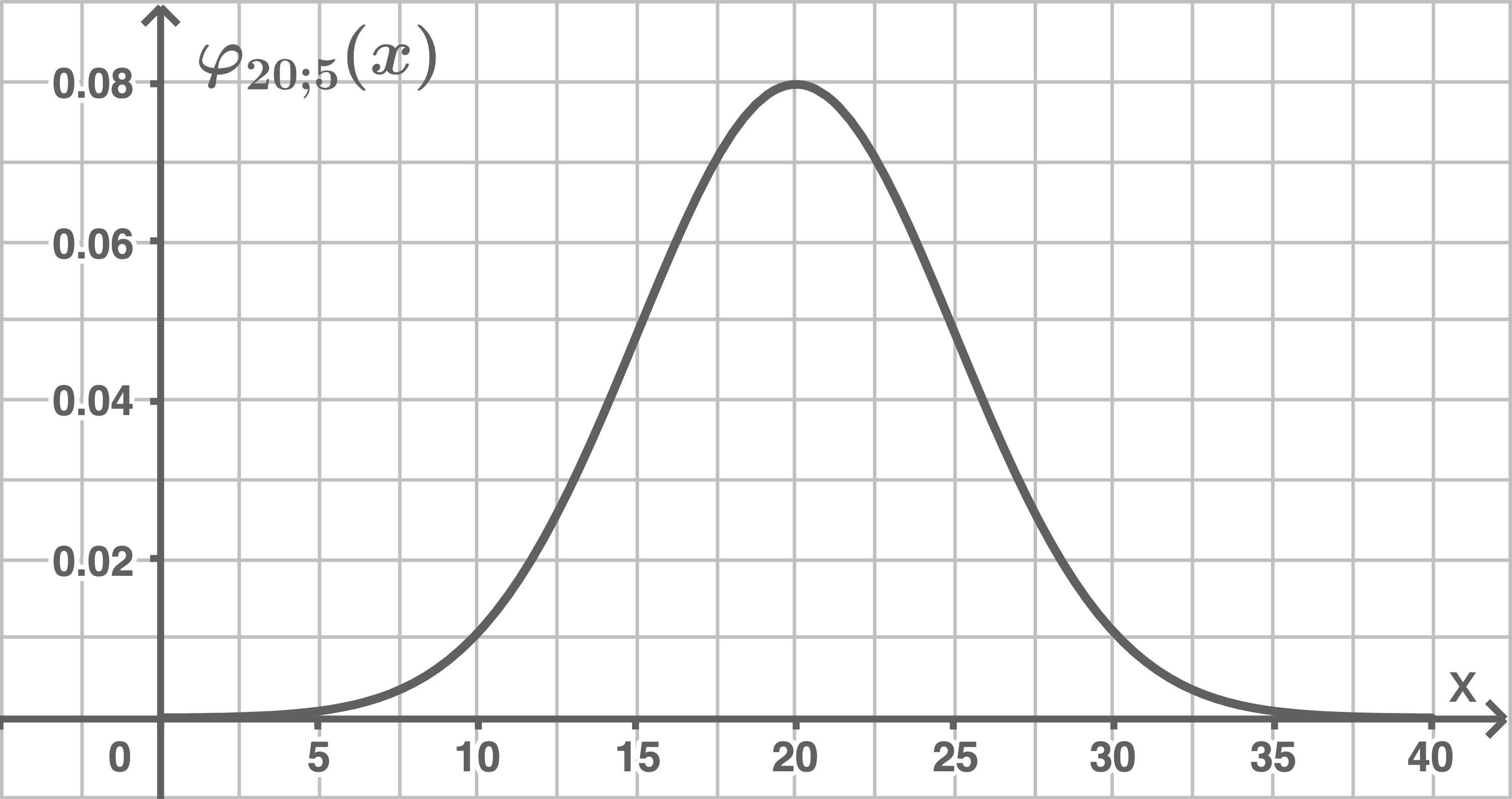Normalverteilung zeichnen Lösung Stochastik BF

Es ist $P(X\leq 20)=0,5.$ Der Inhalt der Fläche, die die Glockenkurve mit der $x-$ Achse im Intervall $[0;20]$ einschließt, entspricht genau der Hälfte des Inhalts der Fläche, die die Glockenkurve insgesamt mit der $x-$ Achse einschließt.

Wenn $\mu$ größer wird, wird die Glockenkurve entlang der $x$ -Achse in positive Richtung verschoben, da bei $x= \mu$ das Maximum ist. An der Form der Glockenkurve ändert sich nichts.

Wenn $\mu$ kleiner wird, wird die Glockenkurve entlang der $x$ -Achse in negative Richtung verschoben.

Wenn $\sigma$ größer wird, wird die Glockenkurve in $x$ -Richtung gestreckt und in $y$ -Richtung gestaucht, denn der Flächeninhalt unter der Kurve bleibt gleich. Das Maximum bleibt bei $x= \mu.$

Wenn $\sigma$ kleiner wird, wird die Glockenkurve in $x$ -Richtung gestaucht und in $y$ -Richtung gestreckt.

Gemeinsamkeiten Binomialverteilung und Normalverteilung

Die Glockenkurve und das Histogramm der Binomialverteilung haben eine ähnliche Form.
An der Glockenkurve können der Erwartungswert und die Standardabweichung abgelesen werden. Für die Binomialverteilung sind die Anzahl der Treffer $k$ und die Gesamtanzahl $n$ relevant.
Es gilt: $\mu= n \cdot p$ und $\sigma= \sqrt{n \cdot p \cdot (1-p)}.$

Unterschiede zwischen Binomialverteilung und Normalverteilung

Die Normalverteilung ist eine stetige Wahrscheinlichkeitsverteilung, die alle beliebigen Werte auf einem Intervall annehmen kann.
Die Binomialverteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die nur bestimmte Werte, zB. 0,1,2,3,... auf einem Intervall annehmen kann.
Die Normalverteilung lässt sich mithilfe einer Glockenkurve darstellen, die Binomialverteilung mithilfe eines Histogramms.

Ein Histogramm der Binomialverteilung wird für $p=0,5$ symmetrisch. Der Erwartungswert $\mu$ muss bei beiden Zufallsgrößen übereinstimmen. Es gilt $\mu=20$ und für eine binomialverteilte Zufallsgröße gilt $\mu= n \cdot p.$

$\begin{array}[t]{rll} \mu&=& n \cdot p \\[5pt] 20&=& n \cdot 0,5 &\quad \scriptsize \mid\; \cdot 2 \\[5pt] 40&=& n \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?