A2 – Exponentialfunktion

Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)

Die Abbildung zeigt den Graphen der Funktion $f$ mit $f(x)=\frac{1}{10}x\cdot(3-x) \cdot \mathrm e^x$ und $x\in \mathbb{R}$ .

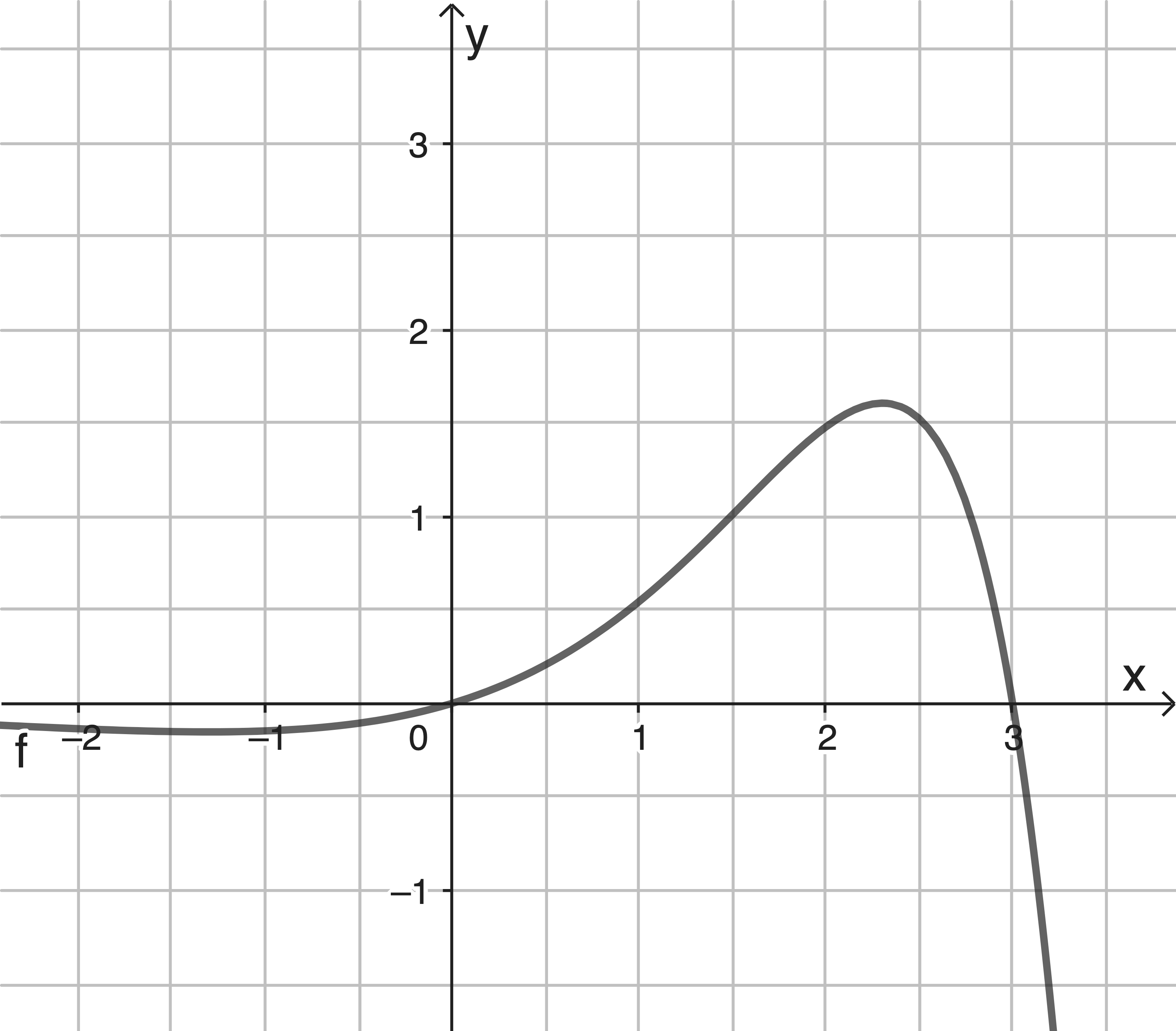Graf einer mathematischen Funktion mit einer Kurve, die über und unter der x-Achse verläuft.

Für die erste Ableitungsfunktion $\(f$ von $f$ gilt $\(f$

Gib die Nullstellen von $f$ an und berechne die x-Koordinate des Hochpunkts des Graphen von $f$ . Hierbei kann auf die Überprüfung der hinreichenden Bedingung verzichtet werden und die Abbildung für die Begründung verwendet werden.

Berechne die Größe des Steigungswinkels des Graphen von $f$ im Koordinatenursprung.

Zeige, dass die in $\mathbb{R}$ definierte Funktion $F$ mit $F(x)=-\dfrac{1}{10}\cdot(x^2-5x+5) \cdot \mathrm e^x$ eine Stammfunktion von $f$ ist.

Begründe ohne zu rechnen, dass es eine positive Zahl $a$ gibt, für die $\displaystyle\int_{0}^{a}f(x)\;\mathrm dx= 0$ gilt.

Begründe ohne Verwendung des Funktionsterms von $F$ , dass der Graph jeder Stammfunktion von $f$ einen Tiefpunkt hat, der auf der y-Achse liegt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Nullstellen angeben

$f(x)=0$

$\frac{1}{10}\cdot x \cdot (3-x) \cdot \mathrm e^x=0$

Das Produkt ist gleich Null, wenn entweder $x_1=0$ oder $x_2=3$ ist (Satz vom Nullprodukt). $\mathrm e^x$ ist immer ungleich Null, sodass es keine weiteren Nullstellen gibt.
Die Nullstellen von $f$ sind $x_1 = 0$ und $x_2 = 3.$

x-Koordinate des Hochpunkts berechnen

$\(f$

$-\dfrac{1}{10}\cdot(x^2-x-3) \cdot \mathrm e^x=0$

$\mathrm e^x\neq 0$ , deshalb wird das Produkt nur dann Null, wenn der Faktor $x^2-x-3$ gleich Null ist (Satz vom Nullprodukt).

$x^2-x-3=0$

$x_{1,2}= -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q}\,$ $=-\dfrac{-1}{2} \pm \sqrt{\left(\dfrac{-1}{2}\right)^2-(-3)}\,$ $=\dfrac{1}{2}\pm\sqrt{\dfrac{1}{4}+3}\,$ $=\dfrac{1}{2}\pm\sqrt{\dfrac{1}{4}+\dfrac{12}{4}}\,$ $=\dfrac{1\pm\sqrt{13}}{2}$

Mithilfe der Abbildung ergibt sich die x-Koordinate des Hochpunkts des Graphen von $f$ mit $x=\frac{1+ \sqrt{13}}{2}.$

Der Steigungswinkel im Koordinatenursprung lässt sich über die Steigung des Graphen von $f$ an der Stelle $x=0$ berechnen.

$\(m=f$ $=0,3$

Berechnung des Steigungswinkels:

$\begin{array}[t]{rll} \tan(\alpha) &=& m \\[5pt] \tan(\alpha) &=& 0,3 \\[5pt] \alpha&\approx& 16,70^{\circ} \end{array}$

Wenn $F$ eine Stammfunktion von $f$ ist, muss $\(F$ gelten.

$F(x)=-\frac{1}{10}\cdot (x^2-5x+5)\cdot \mathrm e^x$

Anwenden der Produktregel:

$\( F$

Vollständigen Rechenweg anzeigen

$x$ ausklammern ergibt:

$\( F$

$(-1)$ mit $(x-3)$ ausmultiplizieren ergibt:

$\(F$

Daraus folgt also $\(F$

Betrachtet wird ein Wert $a\gt 3,$ dann gilt:

$\displaystyle\int_{0}^{a}f(x)\;\mathrm dx = \underbrace{\displaystyle\int_{0}^{3}f(x)\;\mathrm dx}_{\gt 0} +\displaystyle\int_{3}^{a}f(x)\;\mathrm dx$

Das Integral $\displaystyle\int_{3}^{a}f(x)\;\mathrm dx$ beschreibt den Flächeninhalt der Fläche, die der Graph von $f$ im Bereich $3\leq x\leq a$ mit der $x$ -Achse begrenzt.

Diese Fläche liegt allerdings unterhalb der $x$ -Achse, wodurch der Wert des Integrals negativ ist. Je größer der Wert von $a$ gewählt wird, desto größer wird die Fläche und desto größer wird der Betrag des Integralwerts.

Es gibt also definitiv einen Wert von $a,$ für den der Betrag dieses Integrals genauso groß ist, wie der Betrag des ersten Intregrals, sodass der Gesamtwert $\displaystyle\int_{0}^{a}f(x)\;\mathrm dx =0$ beträgt.

$f$ ist die erste Ableitungsfunktion von $F$ und besitzt an der Stelle $x=0$ eine Nullstelle mit Vorzeichenwechsel von negativ zu positiv.

An der Stelle $x=0$ ist also für jede Stammfunktion $F$ von $f$ sowohl das notwendige Kriterium für Extremstellen, als auch das hinreichende Vorzeichenwechselkriterium für Minimalstellen erfüllt.

Damit besitzt der Graph jeder Stammfunktion $F$ von $f$ einen Tiefpunkt, der auf der y-Achse liegt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?