S5 – Erwartungswert
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)
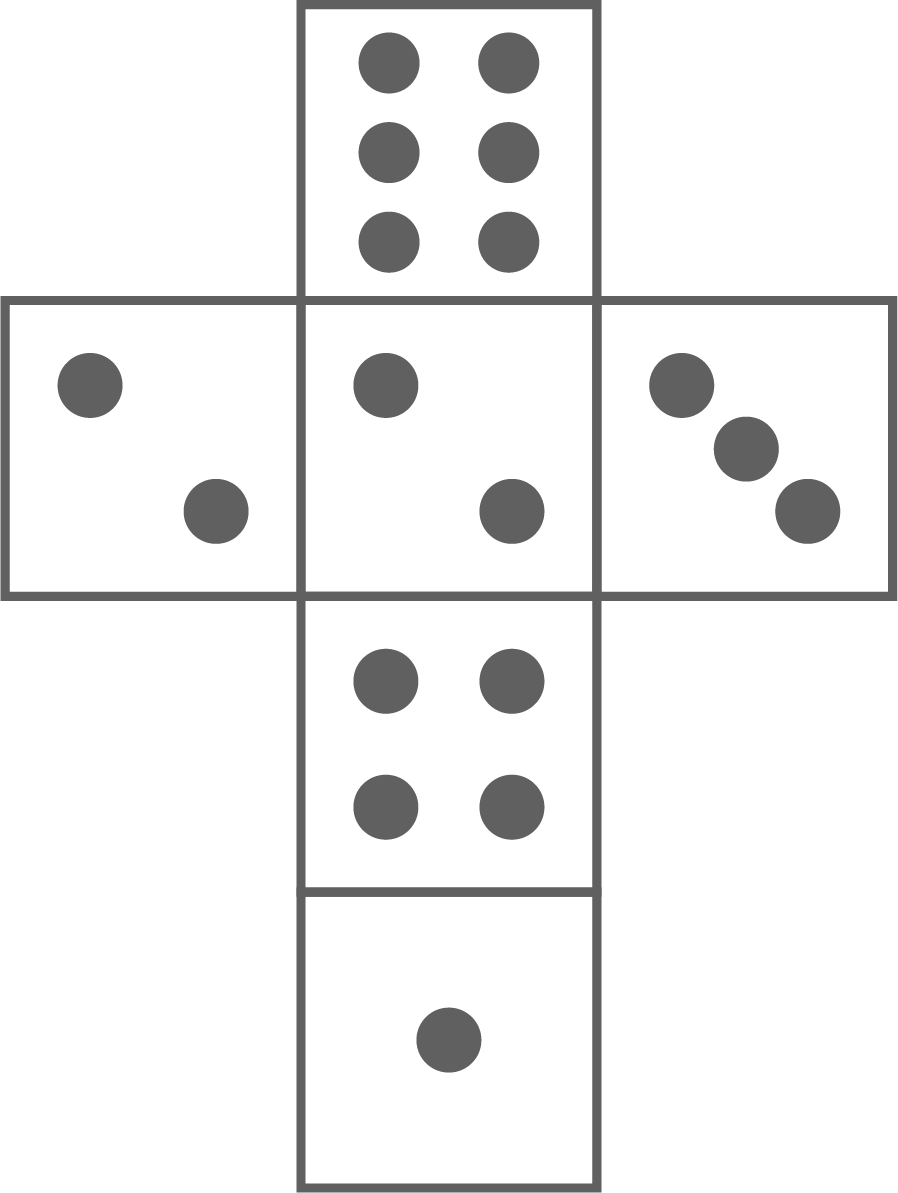
In der Abbildung ist das Netz eines Würfels dargestellt.
Der Würfel wird einmal geworfen. Die Zufallsgröße beschreibt die Augenzahl.
beschreibt die Augenzahl.
Der Würfel wird einmal geworfen. Die Zufallsgröße

a)
Gib die Wahrscheinlichkeit für  an und beschreibe ein Ereignis im Sachzusammenhang.
an und beschreibe ein Ereignis im Sachzusammenhang.
Bestimme den Erwartungswert von
Bestimme den Erwartungswert von
b)
Erläutere die Bedeutung des Erwartungswertes.
c)
Bei einem Glücksspiel darf man für den Einsatz von 1 € einmal würfeln. Wenn dabei die Augenzahl 2 gewürfelt wird, dann erhält man einen Auszahlungsbetrag von 3 €.
Beurteile, ob das Spiel fair ist.
d)
Bestimme die Wahrscheinlichkeit bei zweimaligem Würfeln für die Augensumme 8.
e)
Bei 100-maligem Würfeln werden sechs Sechser geworfen. Beurteile Linas Aussage: „Ich bezweifle, dass der Würfel fair ist.“
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
b)
Der Erwartungswert ist der Mittelwert, wenn ein Zufallsexperiment oft durchgeführt wird. Im Sachzusammenhang bedeutet der Erwartungswert: Wird das Zufallsexperiment häufig durchgeführt, kann davon ausgegangen werden, dass im Mittel die 3 geworfen wird.
c)
Ein Glücksspiel ist fair, wenn im Mittel der Einzahlungsbetrag dem Auszahlungsbetrag entspricht. Der Auszahlungsbetrag  kann
kann  oder
oder  betragen. Das Spiel ist also fair, wenn
betragen. Das Spiel ist also fair, wenn  ist.
ist.
 Somit ist das Spiel fair.
Somit ist das Spiel fair.
d)
Folgende Kombinationen müssen geworfen werden, um auf die Augensumme 8 zu kommen: 4 und 4, 2 und 6, 6 und 2. Mit den Pfadregeln ergibt sich:

e)
Die Wahrscheinlichkeit eine 6 zu werfen, beträgt  und somit 16 %. Bei 100 Würfen ergibt sich der Erwartungswert 16.
Wenn der Würfel fair wäre, könnte im Mittel 16 Mal die Augenzahl 6 erwartet werden. Da die Abweichung zum Erwartungswert relativ groß ist, hat Lina recht und der Würfel ist wahrscheinlich nicht fair.
und somit 16 %. Bei 100 Würfen ergibt sich der Erwartungswert 16.
Wenn der Würfel fair wäre, könnte im Mittel 16 Mal die Augenzahl 6 erwartet werden. Da die Abweichung zum Erwartungswert relativ groß ist, hat Lina recht und der Würfel ist wahrscheinlich nicht fair.