S4 – IQ-Test
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) Im Abi-Jahrgang nehmen 50 Schüler*innen an einem IQ-Test teil.
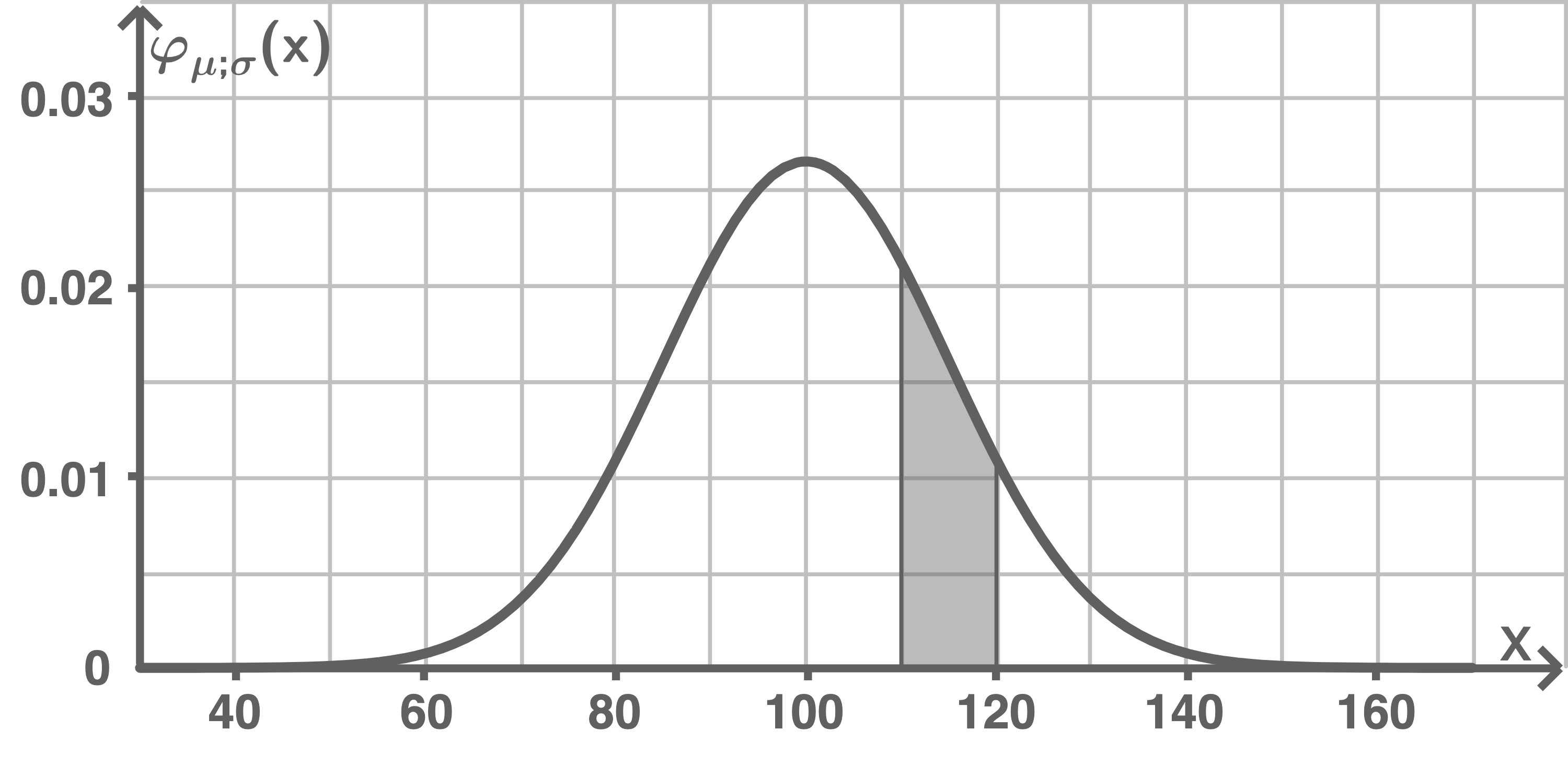 Beurteile: "Der Inhalt der in Abbildung 2 markierten Fläche entspricht der Wahrscheinlichkeit dafür, dass ein*e Schüler*in einen IQ zwischen 100 und 120 hat."
Gib die Wahrscheinlichkeit ohne Rechnung an.
Beurteile: "Der Inhalt der in Abbildung 2 markierten Fläche entspricht der Wahrscheinlichkeit dafür, dass ein*e Schüler*in einen IQ zwischen 100 und 120 hat."
Gib die Wahrscheinlichkeit ohne Rechnung an.
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) Im Abi-Jahrgang nehmen 50 Schüler*innen an einem IQ-Test teil.
| IQ | Anzahl |
|---|---|
| 70 | 0 |
| 85 | 2 |
| 100 | 24 |
| 115 | 21 |
| 130 | 2 |
| 145 | 1 |
a)
Stelle dar, wie der Erwartungswert und die Standardabweichung für den Intelligenzquotienten (IQ) bestimmt werden können.
b)
Der Intelligenzquotient ist normalverteilt mit  und
und 
Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse:
A: „Ein*e Schüler*in hat mindestens einen IQ von 90.“
B: „Der IQ einer Schülerin/eines Schülers weicht um weniger als vom Erwartungswert ab. “
vom Erwartungswert ab. “
Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse:
A: „Ein*e Schüler*in hat mindestens einen IQ von 90.“
B: „Der IQ einer Schülerin/eines Schülers weicht um weniger als
c)
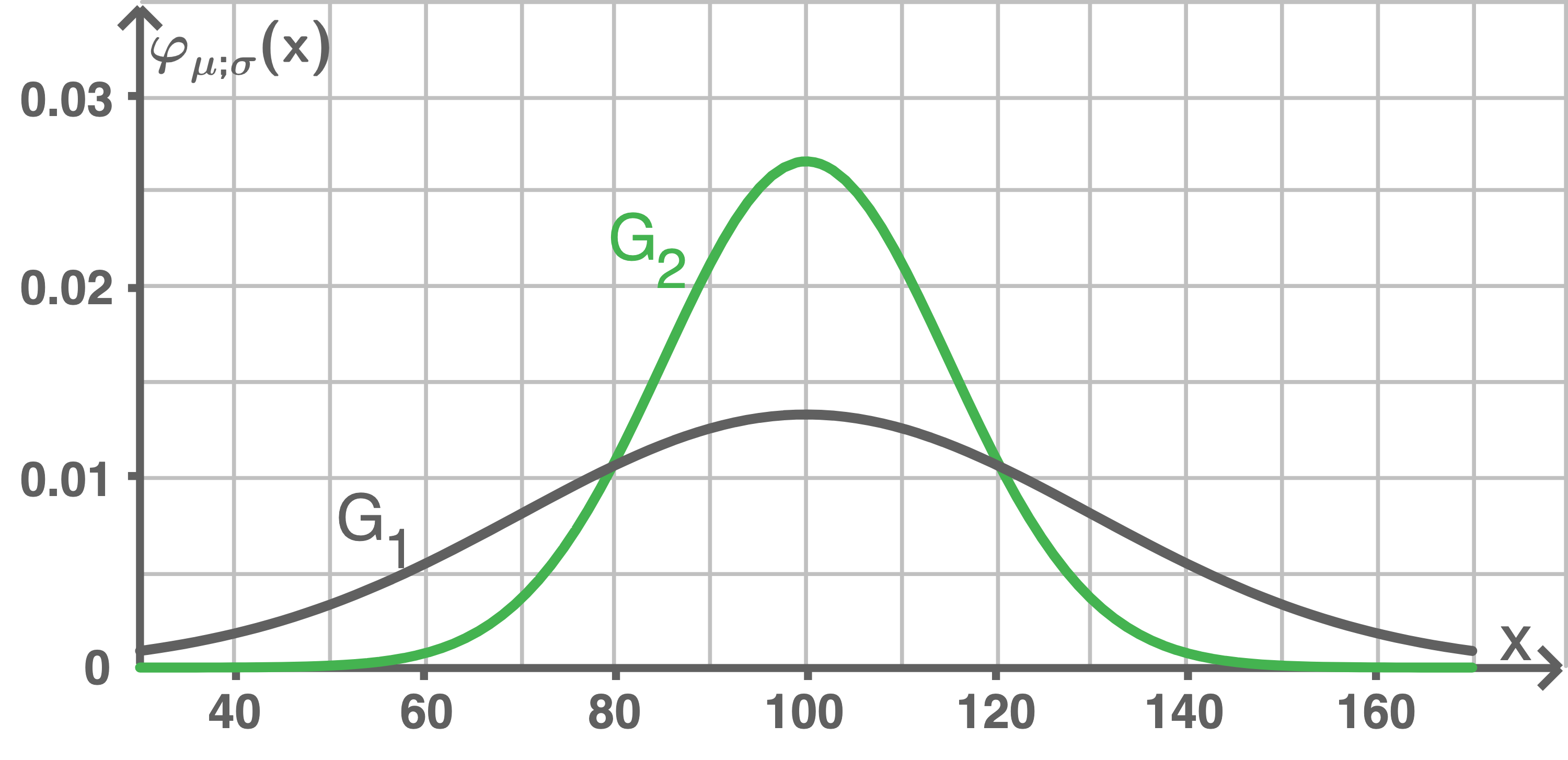
In Abbildung 1 sind mögliche Glockenkurven im Intervall ![\([30; 165]\)](https://www.schullv.de/resources/formulas/532e010968444745a8c71d5e1330c6cf6bd4b0e8903be7b53e6a1afe4800c44f_light.svg) abgebildet, von denen eine den Sachzusammenhang darstellt.
Ordne zu, welcher der beiden Graphen zur Normalverteilung aus Teilaufgabe b) gehört und begründe.
abgebildet, von denen eine den Sachzusammenhang darstellt.
Ordne zu, welcher der beiden Graphen zur Normalverteilung aus Teilaufgabe b) gehört und begründe.
Gib eine Normalverteilung an, zu der der andere Graph gehört.
Gib eine Normalverteilung an, zu der der andere Graph gehört.

Abbildung 1
d)
Beschreibe, wie sich die Glockenkurve ändert, wenn  größer wird, und beschreibe, wie sich die Glockenkurve ändert, wenn
größer wird, und beschreibe, wie sich die Glockenkurve ändert, wenn  größer wird.
größer wird.
e)

Abbildung 2
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Der Erwartungswert  für den IQ ergibt sich, indem die angegebenen IQ-Werte mit der zugehörigen Anzahl an Schüler*innen multipliziert, die Ergebnisse addiert und dann durch die Gesamtanzahl der Schüler*innen geteilt werden.
Die Standardabweichung
für den IQ ergibt sich, indem die angegebenen IQ-Werte mit der zugehörigen Anzahl an Schüler*innen multipliziert, die Ergebnisse addiert und dann durch die Gesamtanzahl der Schüler*innen geteilt werden.
Die Standardabweichung  berechnet sich folgendermaßen: Es wird die Abweichung der einzelnen IQ-Werte vom Erwartungswert bestimmt, dann quadriert und mit der zugehörigen Wahrscheinlichkeit multipliziert, die Ergebnisse dann addiert und daraus wird die Wurzel gezogen.
berechnet sich folgendermaßen: Es wird die Abweichung der einzelnen IQ-Werte vom Erwartungswert bestimmt, dann quadriert und mit der zugehörigen Wahrscheinlichkeit multipliziert, die Ergebnisse dann addiert und daraus wird die Wurzel gezogen.
b)
Die Zufallsvariable  wird für den IQ festgelegt und ist normalverteilt mit
wird für den IQ festgelegt und ist normalverteilt mit  und
und  Die Wahrscheinlichkeiten der Ereignisse ergeben sich mit der kumulierten Normalverteilung mit dem WTR.
Die Wahrscheinlichkeiten der Ereignisse ergeben sich mit der kumulierten Normalverteilung mit dem WTR.

c)
Das Maximum der beiden Graphen liegt an der Stelle  Einsetzen in
Einsetzen in  ergibt den Maximalwert.
Graph zuordnen
ergibt den Maximalwert.
Graph zuordnen
Wegen
 lässt sich
lässt sich  der Normalverteilung des IQs zuordnen.
Normalverteilung angeben
der Normalverteilung des IQs zuordnen.
Normalverteilung angeben
Aus der Abbildung lässt sich die linke Wendestelle von an der Stelle
an der Stelle  ablesen. Somit ist
ablesen. Somit ist  Einsetzen in die Dichtefunktion für eine Gegenprobe:
Einsetzen in die Dichtefunktion für eine Gegenprobe:

 Dieser Wert entspricht dem Wert des Maximums, der auch ungefähr aus der Abbildung abgelesen werden kann. Die Normalverteilung
Dieser Wert entspricht dem Wert des Maximums, der auch ungefähr aus der Abbildung abgelesen werden kann. Die Normalverteilung  und
und  gehört zu Graph
gehört zu Graph 
Wegen
Aus der Abbildung lässt sich die linke Wendestelle von
d)
Wenn  größer wird, wird die Glockenkurve entlang der
größer wird, wird die Glockenkurve entlang der  -Achse in positiver Richtung verschoben, da bei
-Achse in positiver Richtung verschoben, da bei  das Maximum ist. An der Form der Glockenkurve ändert sich nichts.
Wenn
das Maximum ist. An der Form der Glockenkurve ändert sich nichts.
Wenn  größer wird, wird die Glockenkurve in
größer wird, wird die Glockenkurve in  -Richtung gestaucht und in
-Richtung gestaucht und in  -Richtung gestreckt, denn der Flächeninhalt unter der Kurve bleibt gleich. Das Maximum bleibt bei
-Richtung gestreckt, denn der Flächeninhalt unter der Kurve bleibt gleich. Das Maximum bleibt bei 
e)
Die Aussage ist falsch. Richtig ist: Der Inhalt der in Abbildung 2 unter der Glockenkurve markierten Fläche entspricht der Wahrscheinlichkeit der kumulierten Normalverteilung und dafür, dass ein*e Schüler*in einen IQ zwischen 110 und 120 hat.
Anhand der Anzahl an Kästchen ergibt sich die Wahrscheinlichkeit dafür, dass ein*e Schüler*in einen IQ zwischen 110 und 120 hat, mit  was
was  entspricht.
entspricht.