A6 – Funktionsgraphen

Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Taschenrechner (WTR)

In den Abbildungen sind die Graphen drei verschiedener Funktionstypen zu sehen: Der Graph einer Exponentialfunktion $f,$ der Graph einer trigonometrischen Funktion $g$ und der Graph einer ganzrationalen Funktion $h.$

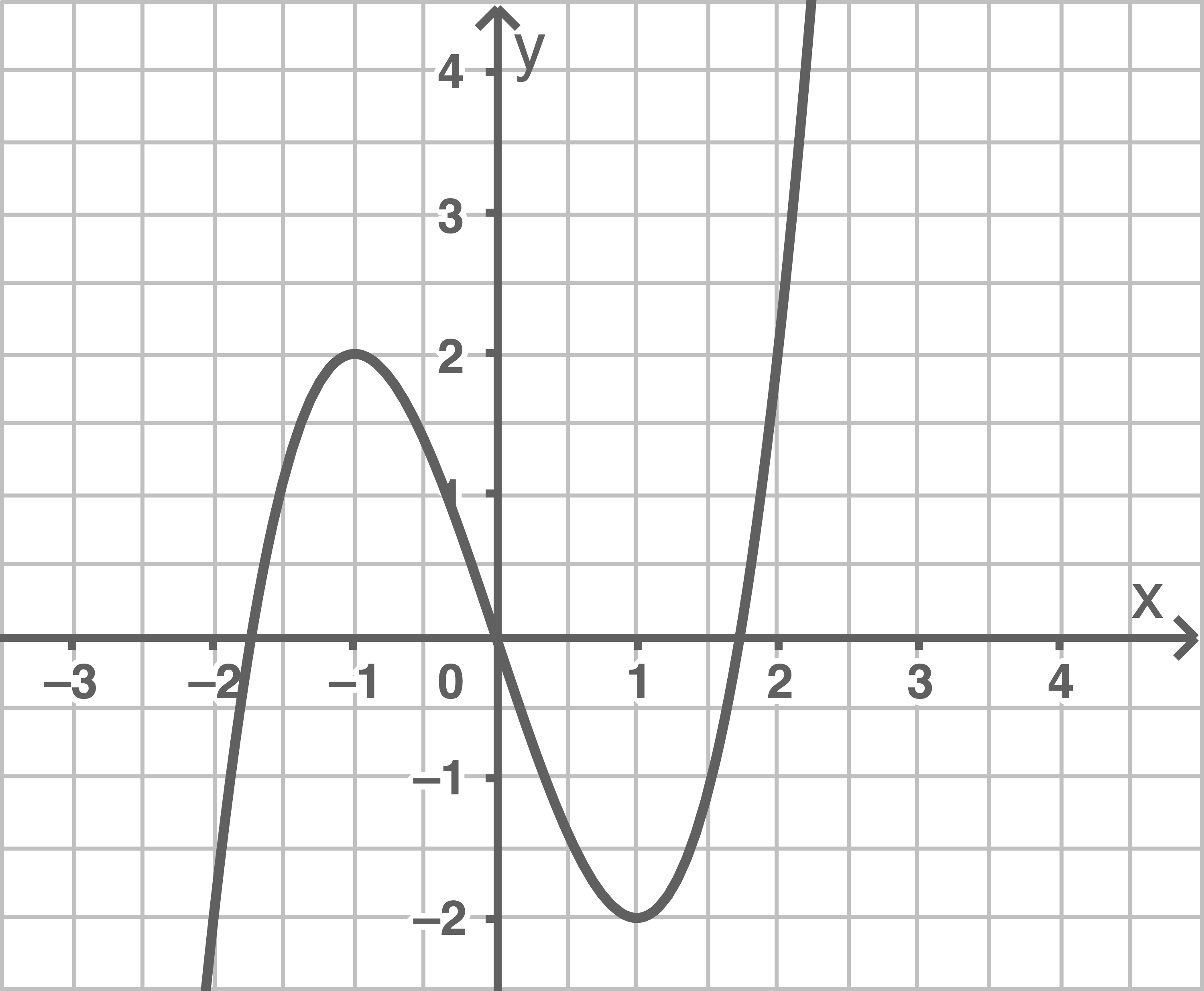
Grafik eines Koordinatensystems mit einer Kurve, die verschiedene Punkte schneidet.

Abbildung 1

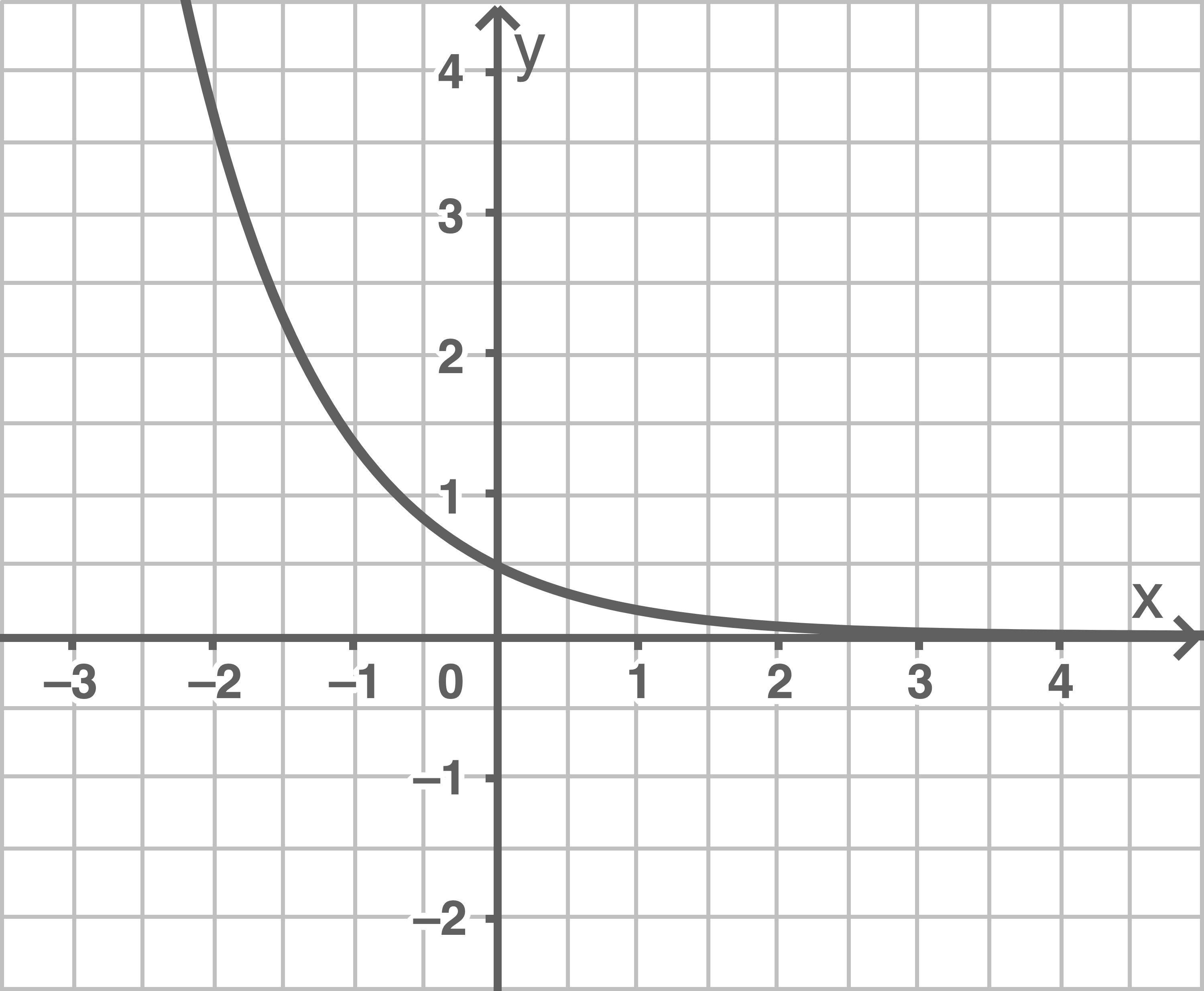
Graf einer Funktion im Koordinatensystem mit Achsenbeschriftung.

Abbildung 2

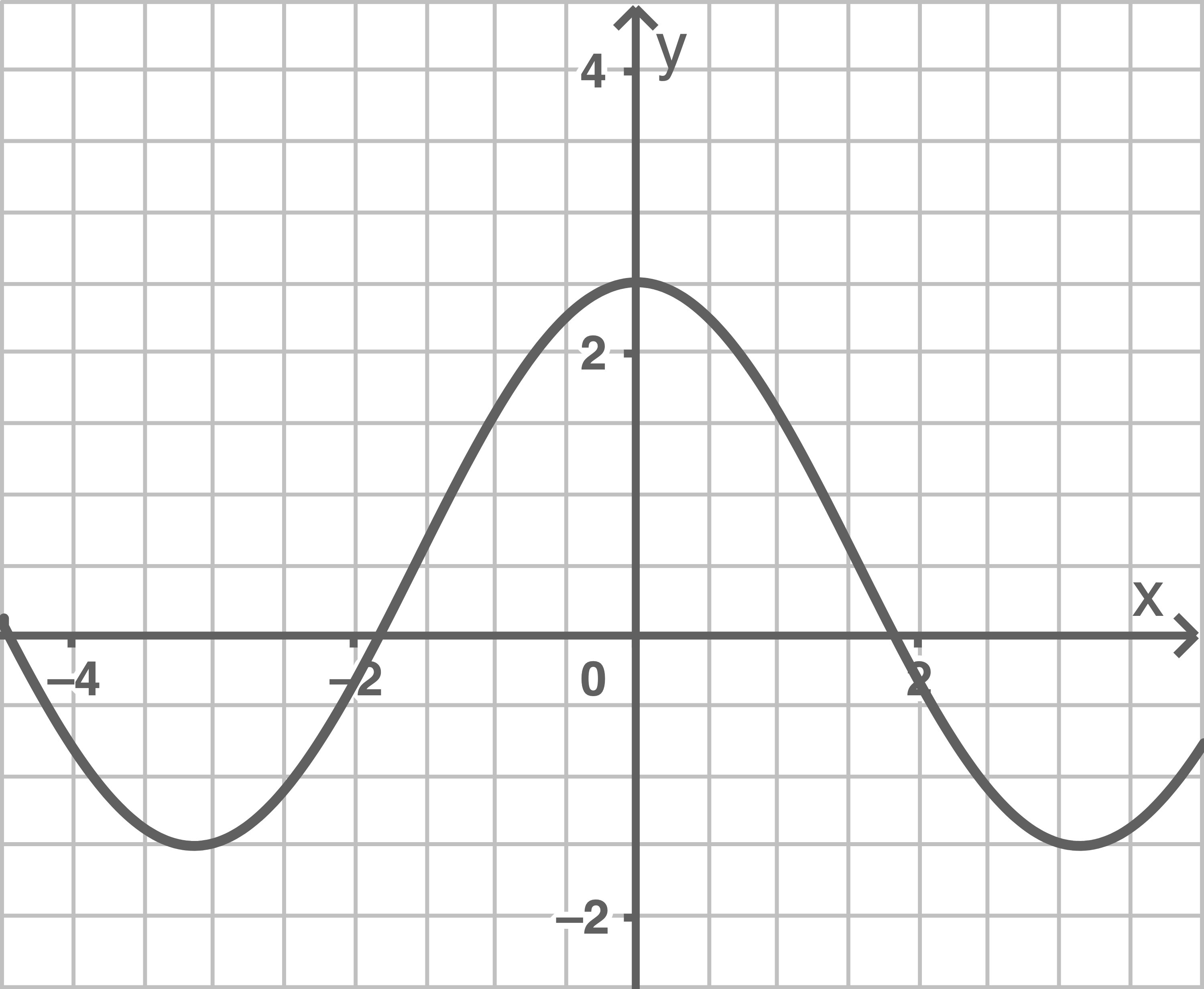
Graph einer mathematischen Funktion im Koordinatensystem mit Achsen und Gitterlinien.

Abbildung 3

Ordne die Funktionen den abgebildeten Graphen zu und begründe.

Gib für den Graphen in Abbildung 2 einen Funktionsterm an und erkläre dein Vorgehen.

Beschreibe, wie der Inhalt der Fläche, die vom Graphen in Abbildung 3 mit der $x$ -Achse im Intervall $[-4;3]$ eingeschlossen wird, berechnet werden kann. Gib einen Term an.

Überprüfe: $\displaystyle\int_{-b}^{b}h(x)\;\mathrm dx=0$

Eine neue Funktion ist mit $d(x)= \mathrm e^{-2x}$ gegeben.

Berechne das $a,$ für das $\displaystyle\int_{a}^{0}d(x)\;\mathrm dx =\dfrac{1}{2}$ gilt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Der Graph in Abbildung 2 ist streng monoton fallend und nähert sich der $x$ -Achse asymptotisch an, deshalb handelt es sich um eine fallende Exponentialfunktion. Die Funktion $f$ kann dem Graphen in Abbildung 2 zugeordnet werden.

In Abbildung 3 ist erkennbar, dass der Graph periodisch verläuft und symmetrisch zur $y$ -Achse ist. Es handelt sich also um eine Kosinusfunktion. Die Funktion $g$ kann somit Abbildung 3 zugeordnet werden.

Der Graph in Abbildung 1 ist punktsymmetrisch zum Ursprung, verläuft für $x\longrightarrow -\infty$ gegen $-\infty$ und für $x\longrightarrow +\infty$ gegen $+ \infty.$ Die Funktion $g$ kann durch Ausschlussverfahren dem Graphen in Abbildung 1 zugeordnet werden.

Ausgangsfunktion: Die an der $y$ -Achse gespiegelte Exponentialfunktion wird durch die Funktion $a(x)=\mathrm e^{-x}$ beschrieben und ihr Graph schneidet die $y$ -Achse im Punkt $(0 \mid 1).$

Aufstellen des Funktionsterms von $h:$ Der Graph von $h$ in der Abbildung schneidet die $y$ -Achse im Punkt $( 0\mid 0,5)$ und nähert sich der $x$ -Achse asymptotisch an. Wird also der Graph der Ausgangsfunktion um $0,5$ in $y$ -Richtung gestaucht, so ergibt sich der Graph von $h.$

Somit folgt der Funktionsterm mit $h(x)= 0,5 \cdot \mathrm e^{-x}.$

Zunächst müssen die Nullstellen von $g$ bestimmt werden. Der Abbildung kann entnommen werden, dass sich im Intervall $[-4;3]$ zwei Nullstellen, $x_1$ und $x_2,$ befinden.
Im nächsten Schritt werden die Inhalte der drei Teilflächen mithilfe von Integralen berechnet und diese Flächeninhalte dann addiert.

$A=\left| \displaystyle\int_{-4}^{x_1}g(x)\;\mathrm dx \right|+ \displaystyle\int_{x_1}^{x_2}g(x)\;\mathrm dx$ $+\left| \displaystyle\int_{x_2}^{3}g(x)\;\mathrm dx \right|$

Der Graph von $h$ ist punktsymmetrisch zum Ursprung. Deshalb gilt $h(-x)=-h(x).$
Der Flächeninhalt der Fläche, die der Graph von $h$ und die $x$ -Achse oberhalb der $x$ -Achse einschließen, ist genauso groß wie der Flächeninhalt der Fläche, die der Graph von $h$ und die $x$ -Achse unterhalb der $x$ -Achse einschließen.

Für den Wert des Flächeninhalts gilt:

$\displaystyle\int_{-b}^{b}h(x)\;\mathrm dx=\displaystyle\int_{-b}^{0}h(x)\;\mathrm dx + \displaystyle\int_{0}^{b}h(x)\;\mathrm dx$

Wegen der Punktsymmetrie zum Koordinatenursprung gilt:

$\displaystyle\int_{-b}^{0}h(x)\;\mathrm dx =-\displaystyle\int_{0}^{b}h(x)\;\mathrm dx$

Damit folgt also:

$\displaystyle\int_{-b}^{b}h(x)\;\mathrm dx=-\displaystyle\int_{0}^{b}h(x)\;\mathrm dx$ $+\displaystyle\int_{0}^{b}h(x)\;\mathrm dx =0$

$\displaystyle\int_{a}^{0}d(x)\;\mathrm dx$ $= \displaystyle\int_{a}^{0} \mathrm e^{-2x} \;\mathrm dx$ $= \left[-\dfrac{1}{2} \cdot \mathrm e^{-2x}\right ]_a^0$ $= -\dfrac{1}{2} \cdot \mathrm e^{-2\cdot 0}- \left(-\dfrac{1}{2} \cdot \mathrm e^{-2 \cdot a} \right)$ $= -\dfrac{1}{2} + \dfrac{1}{2} \cdot \mathrm e^{-2\cdot a}$

Daraus folgt:

$\begin{array}[t]{rll} \displaystyle\int_{0}^{a}d(x)\;\mathrm dx &=& \dfrac{1}{2} \\[5pt] -\dfrac{1}{2}+\dfrac{1}{2} \cdot \mathrm e^{-2\cdot a} &=&\dfrac{1}{2} &\quad \scriptsize \mid\;+\frac{1}{2} \\[5pt] \dfrac{1}{2} \cdot \mathrm e^{-2\cdot a} &=& 1 &\quad \scriptsize \mid\; \cdot 2 \\[5pt] \mathrm e^{-2\cdot a} &=& 2 &\quad \scriptsize \mid\;\ln() \\[5pt] -2\cdot a & = & \ln(2) &\quad \scriptsize \mid\;: (-2) \\[5pt] a & = & -\dfrac{\ln(2)}{2} \\[5pt] a & \approx & -0,35 \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?