A7 – Funktionen
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Taschenrechner (WTR) In der Abbildung sind die Funktionen und
und  dargestellt.
dargestellt.
Vorbereitungszeit: 20 min
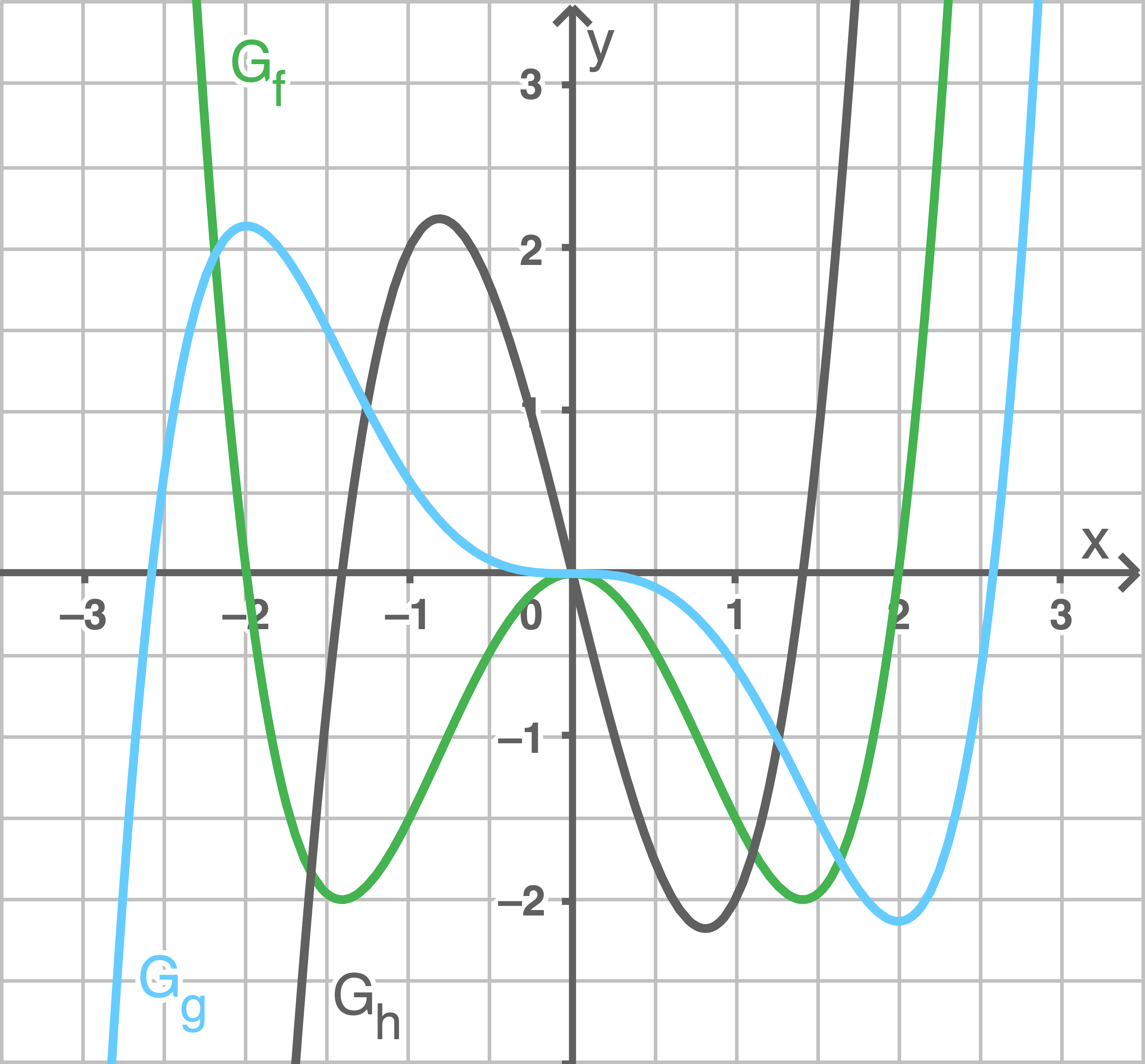
Zugelassene Hilfsmittel: Taschenrechner (WTR) In der Abbildung sind die Funktionen

a)
Eine Funktion ist durch den Funktionsterm  definiert. Ordne dem Funktionsterm einem Graphen aus der Abbildung begründet zu.
Einer der Graphen
definiert. Ordne dem Funktionsterm einem Graphen aus der Abbildung begründet zu.
Einer der Graphen  und
und  beschreibt die Ableitungsfunktion von
beschreibt die Ableitungsfunktion von  und der andere eine Stammfunktion von
und der andere eine Stammfunktion von  Ordne zu und begründe.
Ordne zu und begründe.
b)
Beschreibe, wie der Inhalt der Fläche, die von den Graphen  und
und  eingeschlossen wird, berechnet werden kann. Gib einen Term an.
eingeschlossen wird, berechnet werden kann. Gib einen Term an.
c)
Berechne die Koordinaten der Extrempunkte von 
d)
Überprüfe:  Begründe sowohl graphisch als auch rechnerisch.
Begründe sowohl graphisch als auch rechnerisch.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Der gegebene Funktionsterm entspricht einer ganzrationalen Funktion vierten Grades mit geraden Exponenten. Deshalb muss der Graph symmetrisch zur  -Achse sein. In der Abbildung ist nur ein Graph zu erkennen, der dieses Verhalten aufweist, nämlich der Graph von
-Achse sein. In der Abbildung ist nur ein Graph zu erkennen, der dieses Verhalten aufweist, nämlich der Graph von 
Somit eindeutig durch den Funktionsterm
eindeutig durch den Funktionsterm  beschrieben werden.
beschrieben werden.
 schneidet die
schneidet die  -Achse an den Stellen, an denen
-Achse an den Stellen, an denen  seine Extremstellen hat. Des Weiteren verläuft
seine Extremstellen hat. Des Weiteren verläuft  in den Bereichen unterhalb bzw. oberhalb der
in den Bereichen unterhalb bzw. oberhalb der  -Achse, in denen
-Achse, in denen  streng monoton fallend bzw. streng monoton steigend ist.
streng monoton fallend bzw. streng monoton steigend ist.
Somit entspricht dem Graphen der Ableitungsfunktion von
dem Graphen der Ableitungsfunktion von  Durch Ausschlussverfahren entspricht
Durch Ausschlussverfahren entspricht  dem Graphen einer Stammfunktion von
dem Graphen einer Stammfunktion von 
Somit
Somit entspricht
b)
In der Abbildung ist erkennbar, dass  stets oberhalb von
stets oberhalb von  verläuft. Die beiden Graphen schneiden sich an drei Stellen:
verläuft. Die beiden Graphen schneiden sich an drei Stellen: 
 und
und  Es gibt also zwei Teilflächen, deren Flächeninhalt jeweils mit einem Integral berechnet werden kann.
Da
Es gibt also zwei Teilflächen, deren Flächeninhalt jeweils mit einem Integral berechnet werden kann.
Da  stets oberhalb von
stets oberhalb von  verläuft, ergibt sich die Differenzfunktion mit
verläuft, ergibt sich die Differenzfunktion mit  Daraus folgt der Term
Daraus folgt der Term 
c)
d)
Zwei Möglichkeiten mithilfe der Abbildung
Eine Möglichkeit ist: Zählen der Kästchen der Fläche, die der Graph von  mit der
mit der  -Achse einschließt. Es sind ca. 16 Kästchen und somit ca.
-Achse einschließt. Es sind ca. 16 Kästchen und somit ca. ![\(16 \cdot 0,5 \cdot 0,5 = 4 \;\text{[FE]}.\)](https://www.schullv.de/resources/formulas/76a28fed3df450dfaf53d18b92fa2acc30a925a919b5cb22d6fc68b7381084f4_light.svg) Da die Fläche unterhalb der
Da die Fläche unterhalb der  -Achse liegt, hat der Wert des Integrals ein negatives Vorzeichen. Daraus folgt:
-Achse liegt, hat der Wert des Integrals ein negatives Vorzeichen. Daraus folgt:  Eine weitere Möglichkeit ist: Ablesen der Funktionswerte am Graphen der Stammfunktion
Eine weitere Möglichkeit ist: Ablesen der Funktionswerte am Graphen der Stammfunktion  und Anwendung des Hauptsatzes der Differenzial- und Integralrechnung. Es gilt folglich:
und Anwendung des Hauptsatzes der Differenzial- und Integralrechnung. Es gilt folglich:

 Überprüfung durch Rechnen
Überprüfung durch Rechnen