AG8 – Pyramide
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
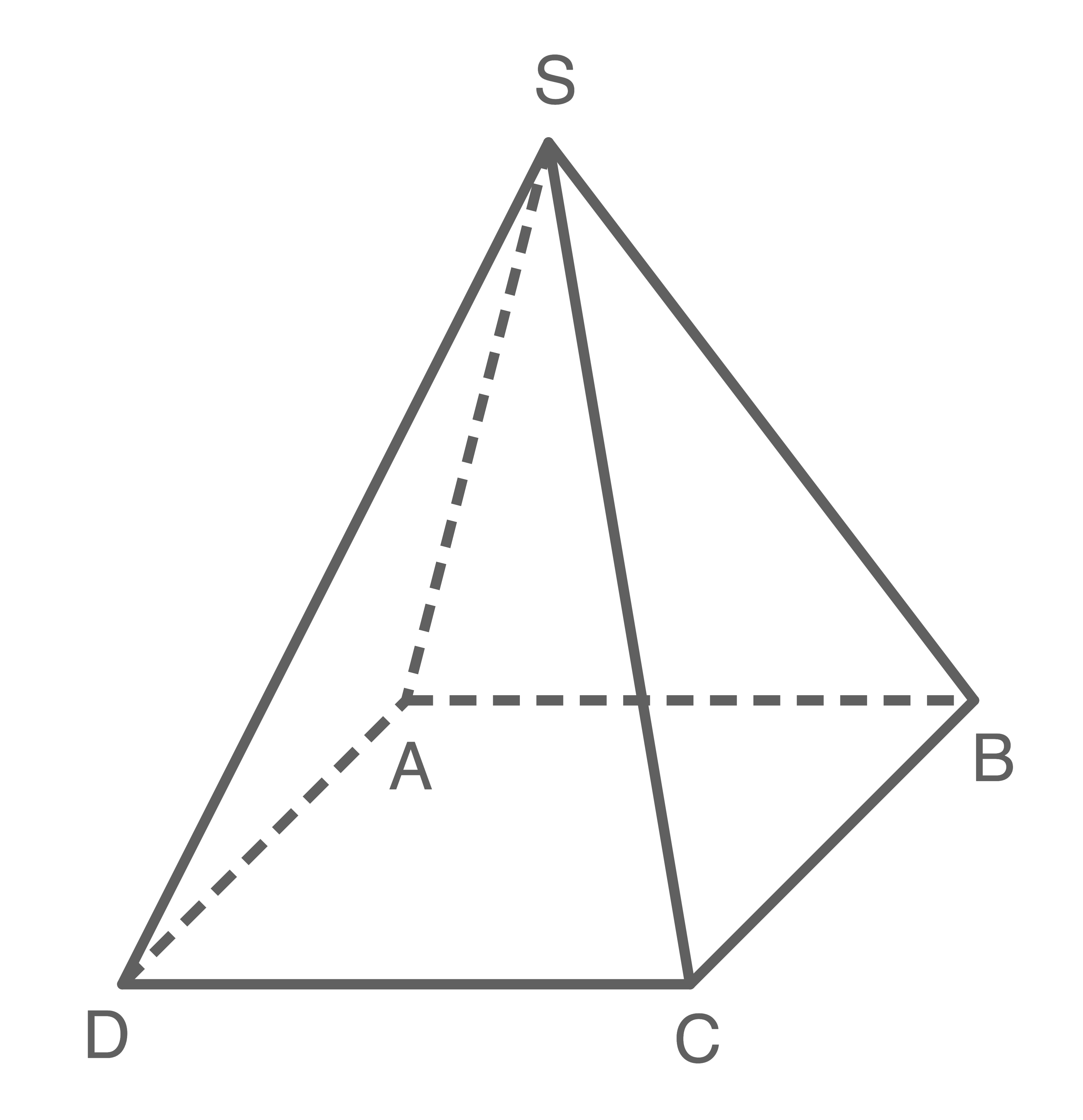
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) Gegeben ist eine quadratische Pyramide ABCDS mit folgendenden Koordinaten:
und 
schneidet die 
-Ebene unter dem Winkel 
Stelle einen Term auf, mit dem 
berechnet werden kann.
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) Gegeben ist eine quadratische Pyramide ABCDS mit folgendenden Koordinaten:
a)
Gib die Koordinaten der fehlenden Punkte 
und 
an.
Stelle eine Ebenengleichung in Koordinatenform auf, die die Punkte 
und 
enthält.
Stelle eine Ebenengleichung
b)
c)
Erkläre, wie das Volumen der Pyramide berechnet wird.
d)
Untersuche, wie die Gleichung einer Ebene 
ermittelt werden kann, die die Ebene senkrecht in der Kante 
schneidet.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Koordinaten der Punkte angeben
und 
Ebenengleichung aufstellen
Es gilt: 
und 
Ein Normalenvektor der Ebene folgt aus:
![\(\begin{array}[t]{rll}
-5x_1+2x_3&=&c &\quad \scriptsize \mid\;\text{B einsetzen} \\[5pt]
-5\cdot 0+2\cdot 0&=& c \\[5pt]
0&=&c
\end{array}\)](https://mathjax.schullv.de/e921d75c663043a5cc2e41108bd79a866d9102716036b01e03ad7c283d9eed52?color=5a5a5a)
Die Ebenengleichung lautet 
b)
Der Winkel zwischen der Ebene und der -Ebene ergibt sich mit Normalenvektoren der Ebenen. Ein Normalenvektor der Ebene ist 
und ein Normalenvektor der -Ebene ist 
Es folgt:
Daraus folgt 
c)
Das Volumen einer Pyramide wird mit 
berechnet.
Aus den Koordinaten lassen sich die Seitenlängen der Grundfläche der Pyramide und die Höhe der Pyramide ablesen. Die Pyramide ist 
lang, breit und 
hoch.
Daraus folgt:
![\( \approx 26,6 \;\text{[VE]}\)](https://mathjax.schullv.de/caa863186d500bb673276141c74918b6b8f0631073cc47ef027c530aa60194cc?color=5a5a5a)
Daraus folgt:
d)
Zunächst muss ein Stützpunkt zB. 
gewählt werden. Die Spannvektoren der Ebene sind 
und 
Damit kann eine Ebenengleichung aufgestellt werden.