A5 – Palme
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Taschenrechner (WTR) Betrachtet wird das Wachstum einer Palme.
Ihre Höhe beträgt zu Beobachtungsbeginn einen Meter, die momentane Wachstumsgeschwindigkeit ihrer Höhe wird durch die Funktion mit
mit  ;
; 
( in Jahren nach Beobachtungsbeginn,
in Jahren nach Beobachtungsbeginn,  in Metern pro Jahr) beschrieben.
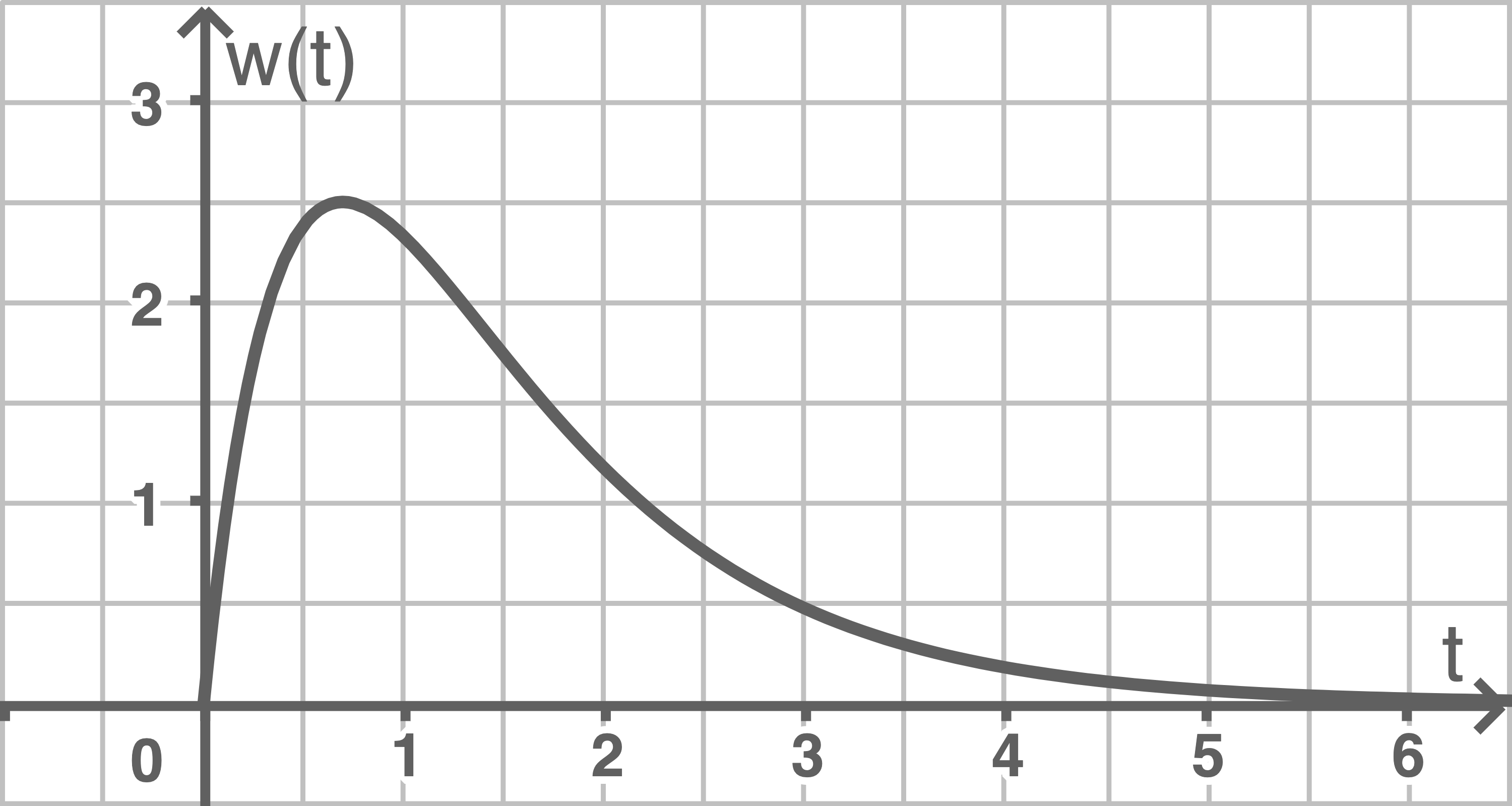
Die Abbildung zeigt den Graphen von
in Metern pro Jahr) beschrieben.
Die Abbildung zeigt den Graphen von 
 beschreibt im folgenden die Höhe der Palme zum Zeitpunkt
beschreibt im folgenden die Höhe der Palme zum Zeitpunkt  (in Jahren nach Beobachtungsbeginn).
Formuliere eine Fragestellung im Sachzusammenhang, die auf die Gleichung
(in Jahren nach Beobachtungsbeginn).
Formuliere eine Fragestellung im Sachzusammenhang, die auf die Gleichung  führt.
führt.
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Taschenrechner (WTR) Betrachtet wird das Wachstum einer Palme.
Ihre Höhe beträgt zu Beobachtungsbeginn einen Meter, die momentane Wachstumsgeschwindigkeit ihrer Höhe wird durch die Funktion
(

a)
Berechne  an der Stelle
an der Stelle  und interpretiere den Wert im Sachzusammenhang.
und interpretiere den Wert im Sachzusammenhang.
b)
Begründe anhand des Verlaufs des Graphen, dass die Höhe der Palme im abgebildeten Zeitraum nie abnimmt.
c)
Gib den Zeitpunkt an, zu dem die Palme ungefähr eine Höhe von 5 Metern hat.
d)
Zeige, dass  eine Stammfunktion von
eine Stammfunktion von  ist.
Berechne die Höhe der Palme im zweiten Jahr nach Beobachtungsbeginn.
ist.
Berechne die Höhe der Palme im zweiten Jahr nach Beobachtungsbeginn.
e)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Mit dem WTR ergibt sich 
 Die momentane Wachstumsgeschwindigkeit wird durch die Funktion
Die momentane Wachstumsgeschwindigkeit wird durch die Funktion  modelliert. Also wächst die Palme 1,5 Jahre nach Beobachtungsbeginn mit einer Geschwindigkeit von 1,73 Metern pro Jahr.
modelliert. Also wächst die Palme 1,5 Jahre nach Beobachtungsbeginn mit einer Geschwindigkeit von 1,73 Metern pro Jahr.
b)
Die Höhe der Palme nimmt im abgebildeten Zeitraum nie ab, da der Graph der Funktion  im abgebildeten Zeitraum nur oberhalb der
im abgebildeten Zeitraum nur oberhalb der  -Achse verläuft. Somit ist die Wachstumsgeschwindigkeit im abgebildeten Zeitraum stets positiv.
-Achse verläuft. Somit ist die Wachstumsgeschwindigkeit im abgebildeten Zeitraum stets positiv.
c)
Zu Beobachtungsbeginn hat die Palme eine Höhe von einem Meter. Folglich muss die Stelle  gefunden werden, für die der Inhalt der Fläche, die der Graph und die
gefunden werden, für die der Inhalt der Fläche, die der Graph und die  -Achse im Intervall
-Achse im Intervall ![\([0;t]\)](https://www.schullv.de/resources/formulas/44bd19c8d46989227acb5541af2f57f3aeeebafc33e9b850dd8e6e31071537c1_light.svg) einschließen, vier Flächeneinheiten ergibt.
Eine Flächeneinheit besteht aus vier Kästchen.
Also werden 16 Kästchen benötigt. Dies ist im Intervall
einschließen, vier Flächeneinheiten ergibt.
Eine Flächeneinheit besteht aus vier Kästchen.
Also werden 16 Kästchen benötigt. Dies ist im Intervall ![\([0; 2,25]\)](https://www.schullv.de/resources/formulas/2b28586b2febc8666cba09b95352d6cec3fd41f8a83be45311b9ccd8c036d5d3_light.svg) der Fall.
Nach ungefähr 2,25 Jahren hat die Palme eine Höhe von 5 Metern.
der Fall.
Nach ungefähr 2,25 Jahren hat die Palme eine Höhe von 5 Metern.
d)
Nachweis der Stammfunktion
Höhe der Palme im zweiten Jahr
e)
„In welchem Halbjahreszeitraum nimmt die Höhe der Palme um 50 % zu?“