A3 – Kostenfunktion
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)
Die Kosten, die einem Unternehmen bei der Herstellung einer Flüssigkeit entstehen, können durch die Funktion 
mit 
und ![\( x\in [0;9]\)](https://mathjax.schullv.de/89a661ee3f2e6353513abf26ef071e33856586d072bf9098023e15aa6bfec9e5?color=5a5a5a)
beschrieben werden.
Dabei gibt 
die Kosten in 1.000 Euro an, die bei der Produktion von 
Kubikmetern der Flüssigkeit insgesamt entstehen.
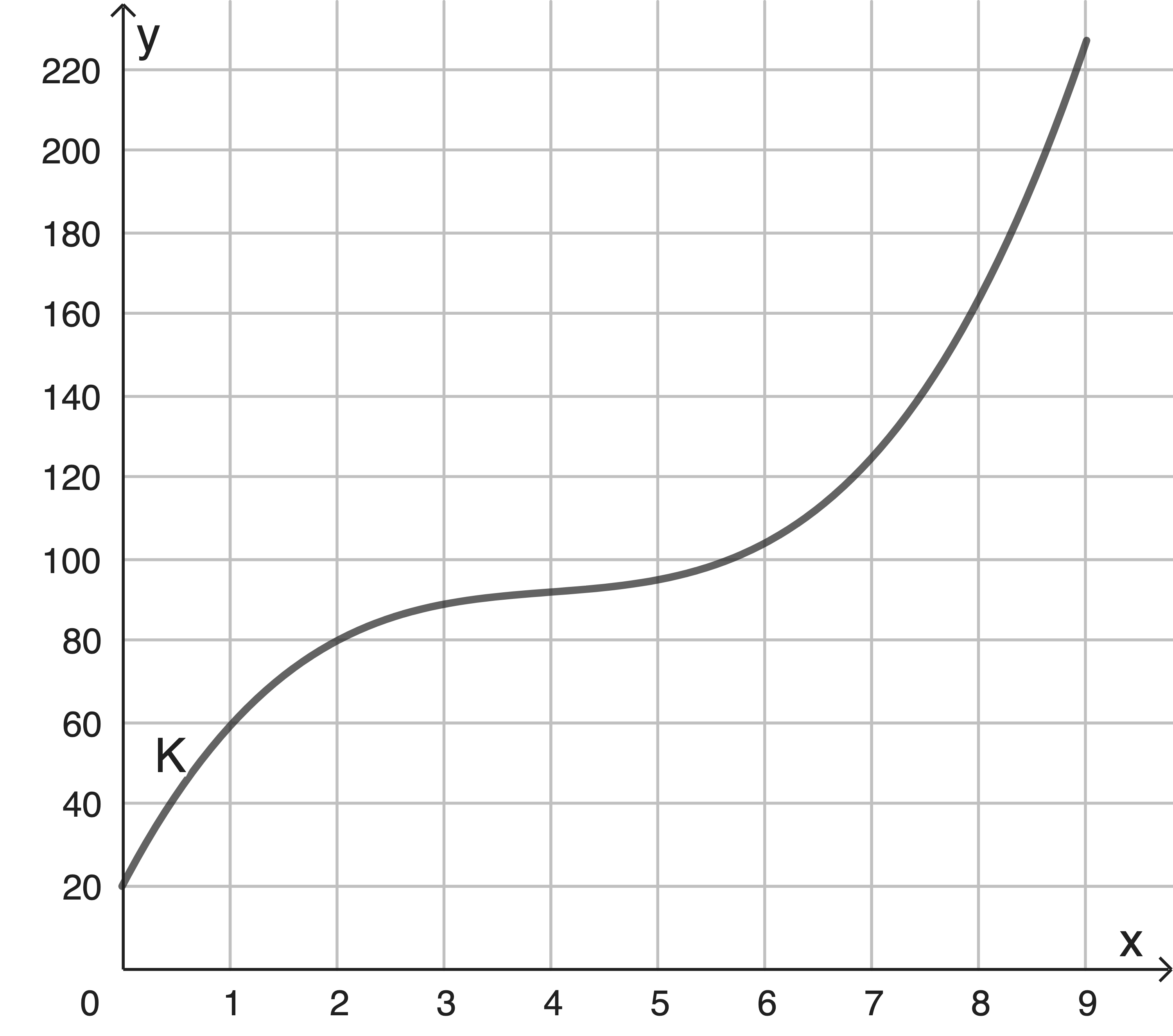
Die Abbildung zeigt den Graphen von
Die Abbildung zeigt den Graphen von
a)
Gib mithilfe der Abbildung die Produktionsmenge an, bei der die Kosten 125.000 Euro betragen.
b)
Gib das Monotonieverhalten von an und deute deine Angabe im Sachzusammenhang.
c)
Beurteile die folgende Aussage:
Je größer die Produktionsmenge ist, desto höher sind die Kosten, die die Produktion eines zusätzlichen Kubikmeters der Flüssigkeit verursacht.
Je größer die Produktionsmenge ist, desto höher sind die Kosten, die die Produktion eines zusätzlichen Kubikmeters der Flüssigkeit verursacht.
d)
Wenn 
die Erlösfunktion ist, wie lautet dann die Gewinnfunktion 
? Wie hoch ist der Gewinn bei der Produktion von sechs Kubikmetern?
e)
Wie könnte man die Produktionsmenge berechnen, bei welcher der größtmögliche Gewinn erzielt wird?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
In der Abbildung ist die Schnittstelle des Graphen mit der Geraden 
gesucht.
Diese lässt sich bei
ablesen.
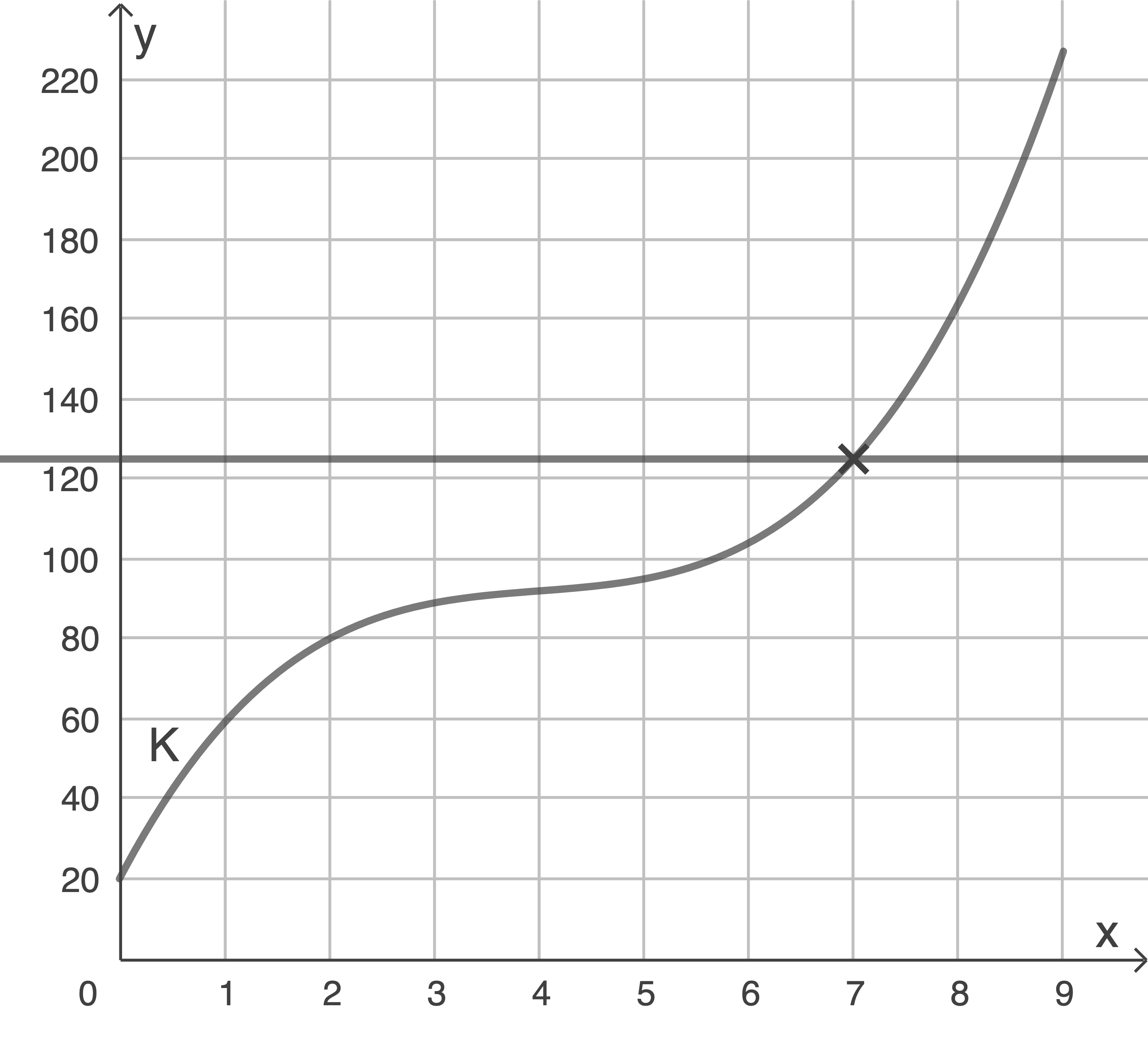Bei einer Produktionsmenge von ca. sieben Kubikmetern Flüssigkeit fallen 125.000 Euro Kosten an.
Diese lässt sich bei
b)
Der Abbildung lässt sich entnehmen, dass 
für 
monoton steigt.
Die Kosten steigen also mit der Menge der produzierten Flüssigkeit.
Die Kosten steigen also mit der Menge der produzierten Flüssigkeit.
c)
Bei Produktionseinheiten werden die Kosten eines zusätzlichen Kubikmeters durch die Differenz 
beschrieben.
Damit die Behauptung aus der Aufgabenstellung stimmt, müsste 
streng monoton steigend sein. Dies ist der Fall, wenn 
ist.
Die Behauptung aus der Aufgabenstellung ist also nur für Produktionsmengen über 3,5 Kubikmetern der Flüssigkeit richtig.
Für alle Produktionsmengen der Flüssigkeit bis zu 3,5 Kubikmetern steigen die Kosten eines zusätzlichen Kubikmeters nicht mit der Produktionsmenge an.
Für alle Produktionsmengen der Flüssigkeit bis zu 3,5 Kubikmetern steigen die Kosten eines zusätzlichen Kubikmeters nicht mit der Produktionsmenge an.
d)
e)
Gesucht ist die Maximalstelle 
von 
im Bereich 
1. Schritt: Ableitungsfunktionen bilden
![\(\begin{array}[t]{rll}
G(x)&=&-x^3 + 12x^2 - 27x - 20 \\[10pt]
G](https://mathjax.schullv.de/7fdfba83291a0e45009e983abb86fa43379d6311698d8f3a495f9e3c30cb1354?color=5a5a5a)
2. Schritt: Notwendiges Kriterium für Extremstellen anwenden
![\(\begin{array}[t]{rll}
G](https://mathjax.schullv.de/03ccf0e1ac39dbdb8a0c870c8a6cf1c96c2b4a2baafe0846a9e837efa4c342c5?color=5a5a5a)
p-q-Formel anwenden:
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{-8}{2}\pm \sqrt{\left(\dfrac{-8}{2}\right)^2-9 } \\[5pt]
&=& 4\pm\sqrt{7} \\[5pt]
x_1&=& 4-\sqrt{7} \\[5pt]
x_2&=& 4+\sqrt{7}
\end{array}\)](https://mathjax.schullv.de/cc648d175b8e18e72bb020b578c5235a6b985be116260a8aae81047e958e13b7?color=5a5a5a)
3. Schritt: Hinreichendes Kriterium überprüfen
An der Stelle 
besitzt der Graph von einen Hochpunkt.
4. Schritt: Funktionswerte vergleichen
Vergleiche die Funktionswerte an den Intervallrändern mit dem im Hochpunkt:
Es müssen 
Kubikmeter der Flüssigkeit verkauft werden, damit das Unternehmen den größten Gewinn erzielt.