A12 – Trigonometrische Funktionen

Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)

Gegeben ist eine Funktion $f$ mit $f(x)= 1,5 \cdot \sin \left(x+\dfrac{\pi}{2} \right)+2.$

a)

In der Abbildung ist der Graph von $f$ dargestellt.

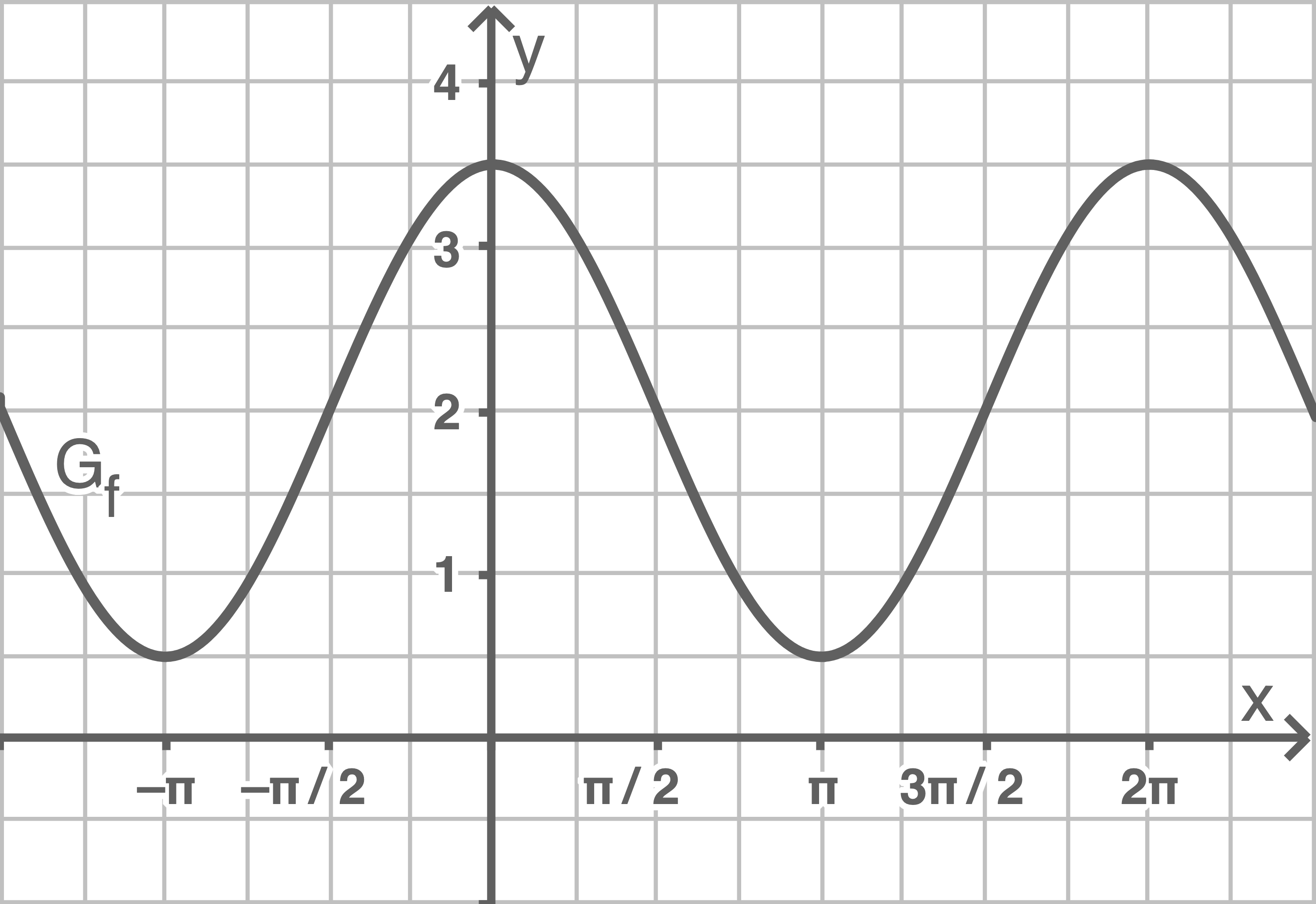sinusfunktion aufgabe basisfach bw abi

Erkläre, wie der Graph von $f$ aus dem Graphen von $\sin(x)$ hervorgeht.

b)

In einer der beiden folgenden Abbildungen ist der Graph der Ableitungsfunktion $\(f$ dargestellt.

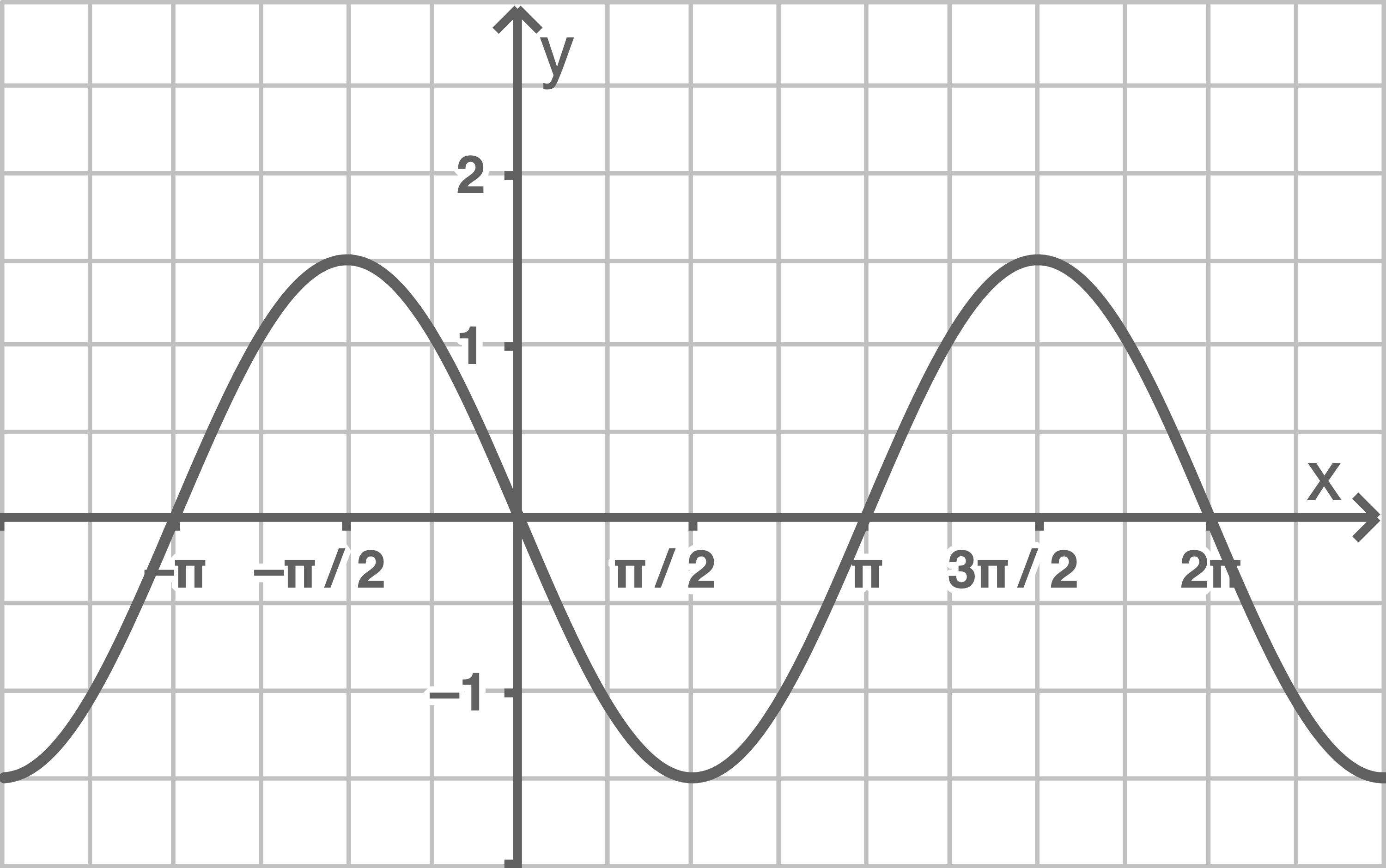
sinusfunktion zuornung basisfach bw abi

Abbildung 1

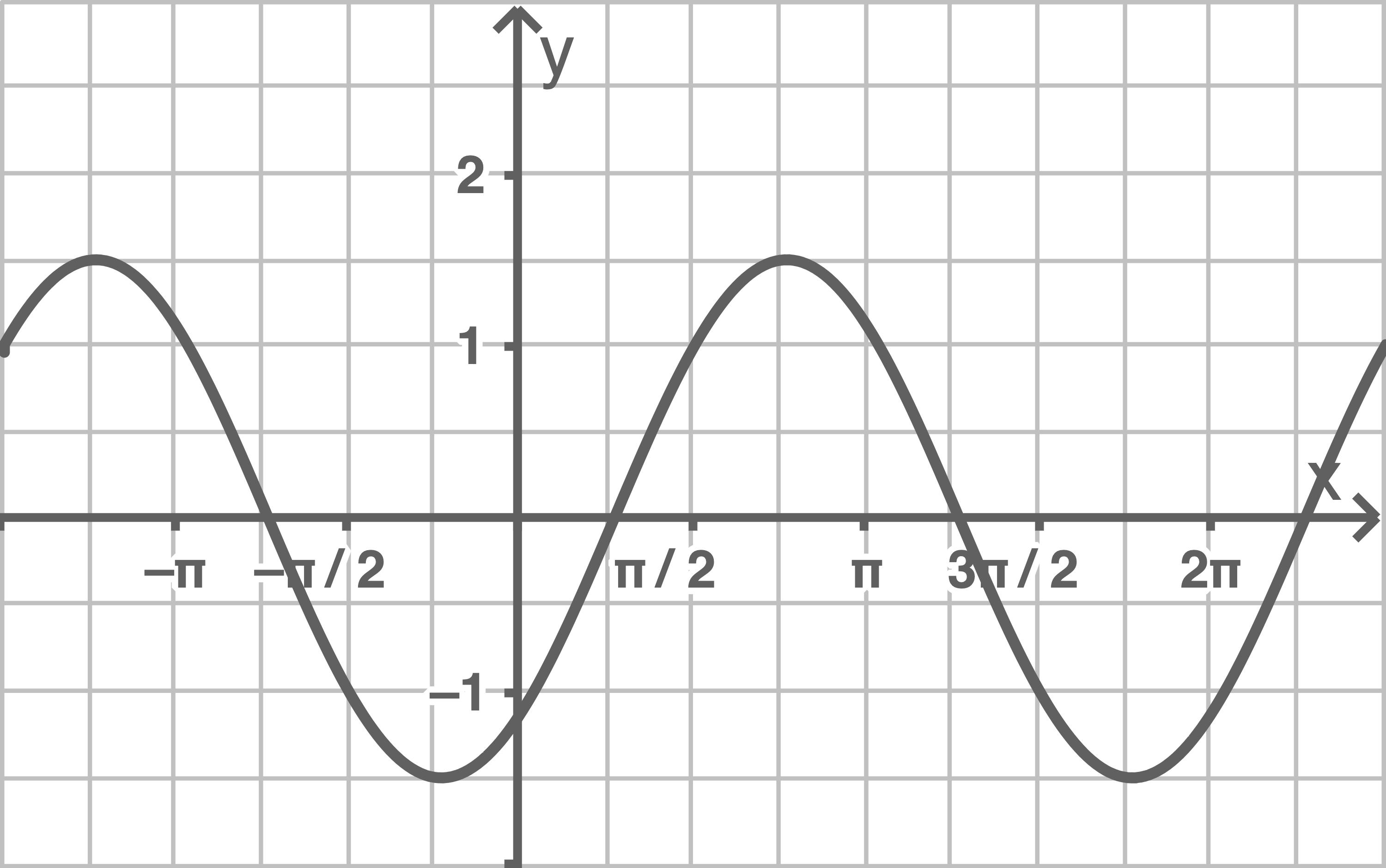sinusfunktion zuornung ableitung bw abi

Abbildung 2

Entscheide begründet, in welcher Abbildung der Graph von $\(f$ dargestellt ist.

c)

Begründe ohne zu rechnen, dass $\(\displaystyle\int_{-\pi}^{\pi}f$ gilt.

d)

Berechne $\displaystyle\int_{0}^{\pi} (f(x)-5) \;\mathrm dx$ und deute das Ergebnis geometrisch.

e)

Beurteile die folgende Aussage:
„Eine trigonometrische Funktion ist durch die Angabe der Koordinaten eines beliebigen Hochpunkts und eines beliebigen Tiefpunkts ihres Graphen eindeutig bestimmt.“

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?