A9 – Ganzrationale Funktion
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
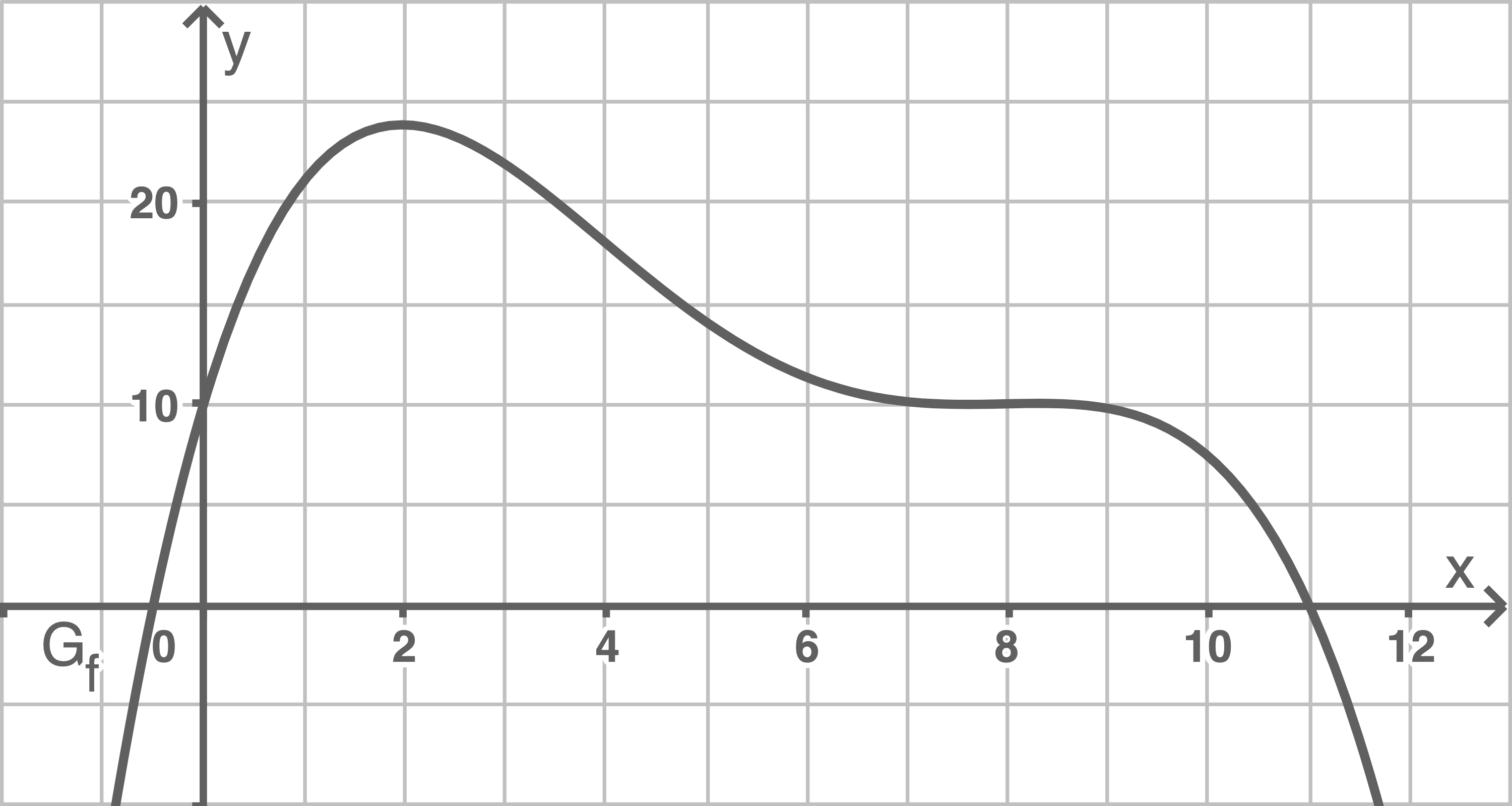
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) Die Abbildung zeigt den Graphen einer in
definierten ganzrationalen Funktion 
vierten Grades. Die Tangente im Wendepunkt 
des Graphen hat die Steigung 
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR) Die Abbildung zeigt den Graphen einer in
a)
Zeichne die beschriebene Tangente ein und berechne die Größe des Winkels, unter dem diese Tangente die 
-Achse schneidet.
b)
Begründe, dass 
außerhalb des abgebildeten Bereichs keine Wendepunkte besitzt.
c)
Gib die beiden Nullstellen der ersten Ableitungsfunktion 
von an.
d)
Der Graph von hat einen Tiefpunkt. Gib die Koordinaten dieses Tiefpunkts an und begründe deine Angabe.
e)
Beurteile die folgende Aussage:
Für jede Stammfunktion 
von gilt 
für jeden Wert von ![\(x\in[0;5].\)](https://mathjax.schullv.de/26a5be3c0e536f83dc20a89ef986c015a5d3ac58d0c085363f74f220eb732bf4?color=5a5a5a)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
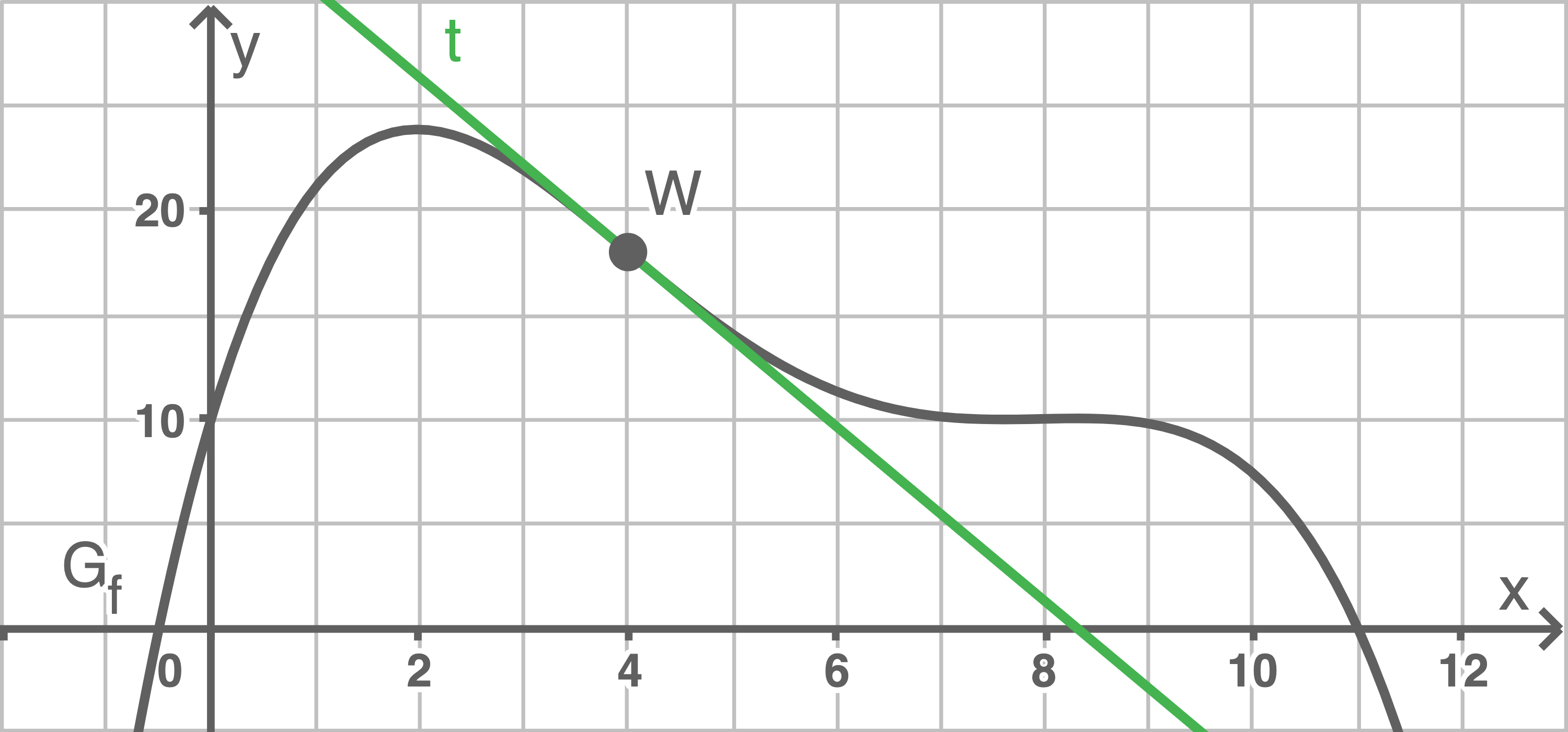
b)
Eine Wendestelle ist mit
Deshalb hat
c)
Die Nullstellen der Ableitungsfunktion sind die Extremstellen der Funktion bzw. die Stellen, an der 
eine waagrechte Tangente hat. Diese lassen sich aus der Abbildung mit 
und 
ablesen.
Die Nullstellen von sind also und 
Die Nullstellen von
d)
Die Stelle an der
Der Abbildung lässt sich entnehmen, dass
In der Aufgabenstellung ist angegeben, dass die Steigung im Wendepunkt
e)