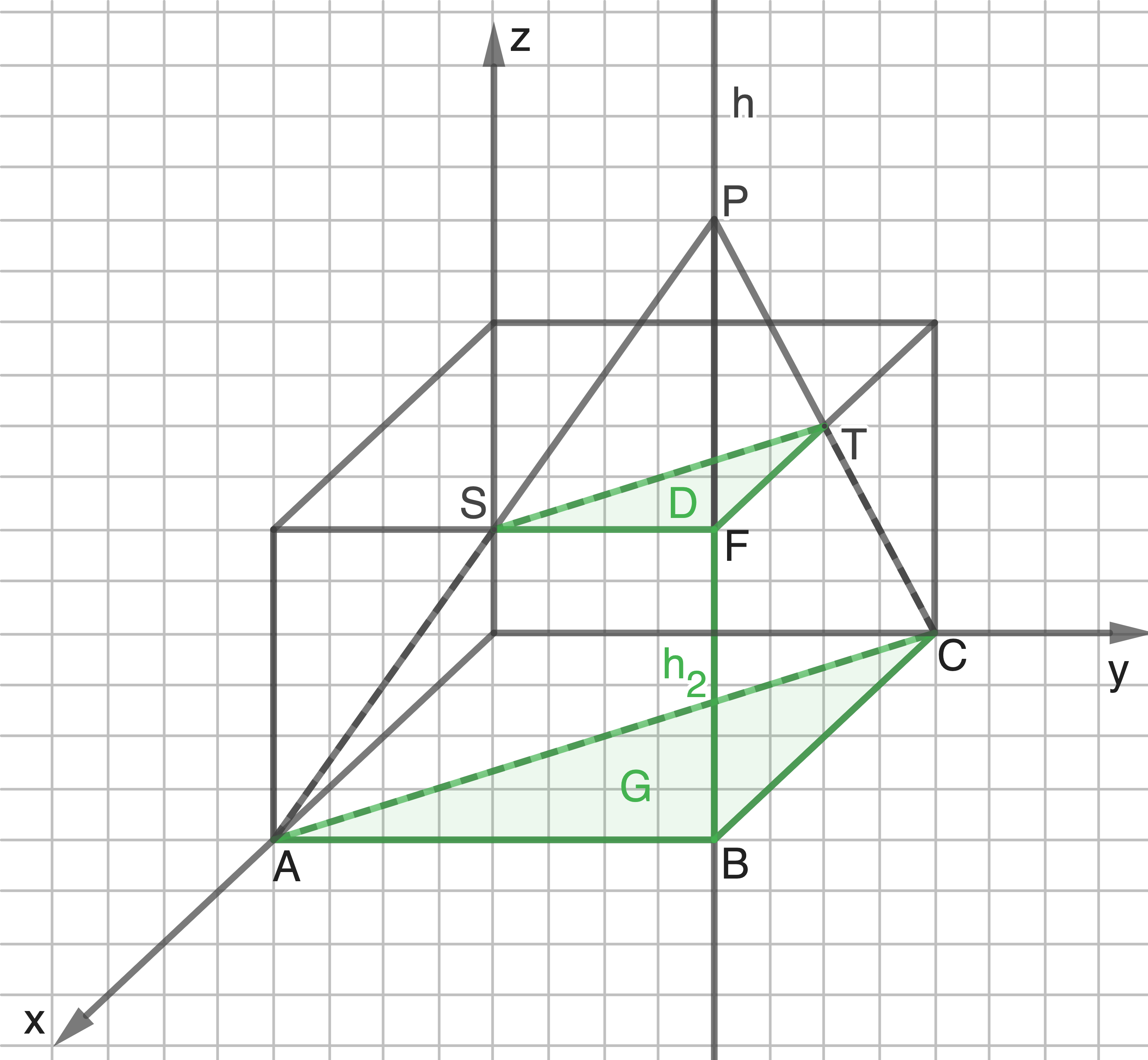
AG1 – Quader
Anmerkung zur Prüfungssituation
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)
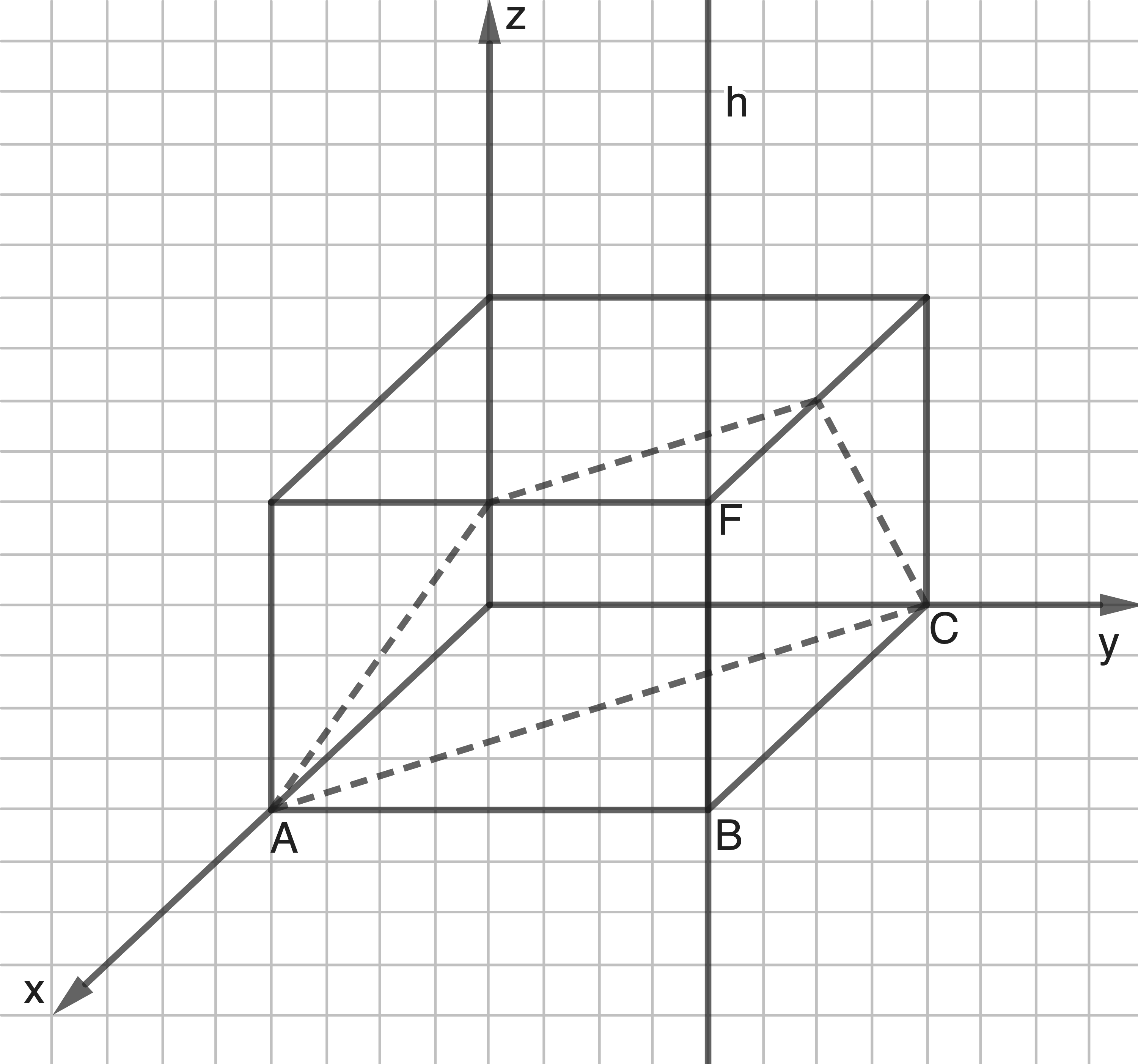
Die Abbildung zeigt gestrichelt die Seiten der Schnittfigur des Quaders und einer Ebene, in der die Punkte
und 
sowie ein Punkt 
der Gerade 
liegen.
Diese Ebene zerlegt den Quader in zwei Teilkörper.
Vorbereitungszeit: 20 min
Zugelassene Hilfsmittel: Merkhilfe & Taschenrechner (WTR)
a)
Begründe, dass das Dreieck 
rechtwinklig und gleichschenklig ist.
Gib den Flächeninhalt dieses Dreiecks an.
Gib den Flächeninhalt dieses Dreiecks an.
b)
Gib eine Gleichung der Geraden an, die durch und verläuft.
Begründe, dass diese Gerade windschief zur Geraden ist.
Begründe, dass diese Gerade windschief zur Geraden
Die Abbildung zeigt gestrichelt die Seiten der Schnittfigur des Quaders und einer Ebene, in der die Punkte
Diese Ebene zerlegt den Quader in zwei Teilkörper.
c)
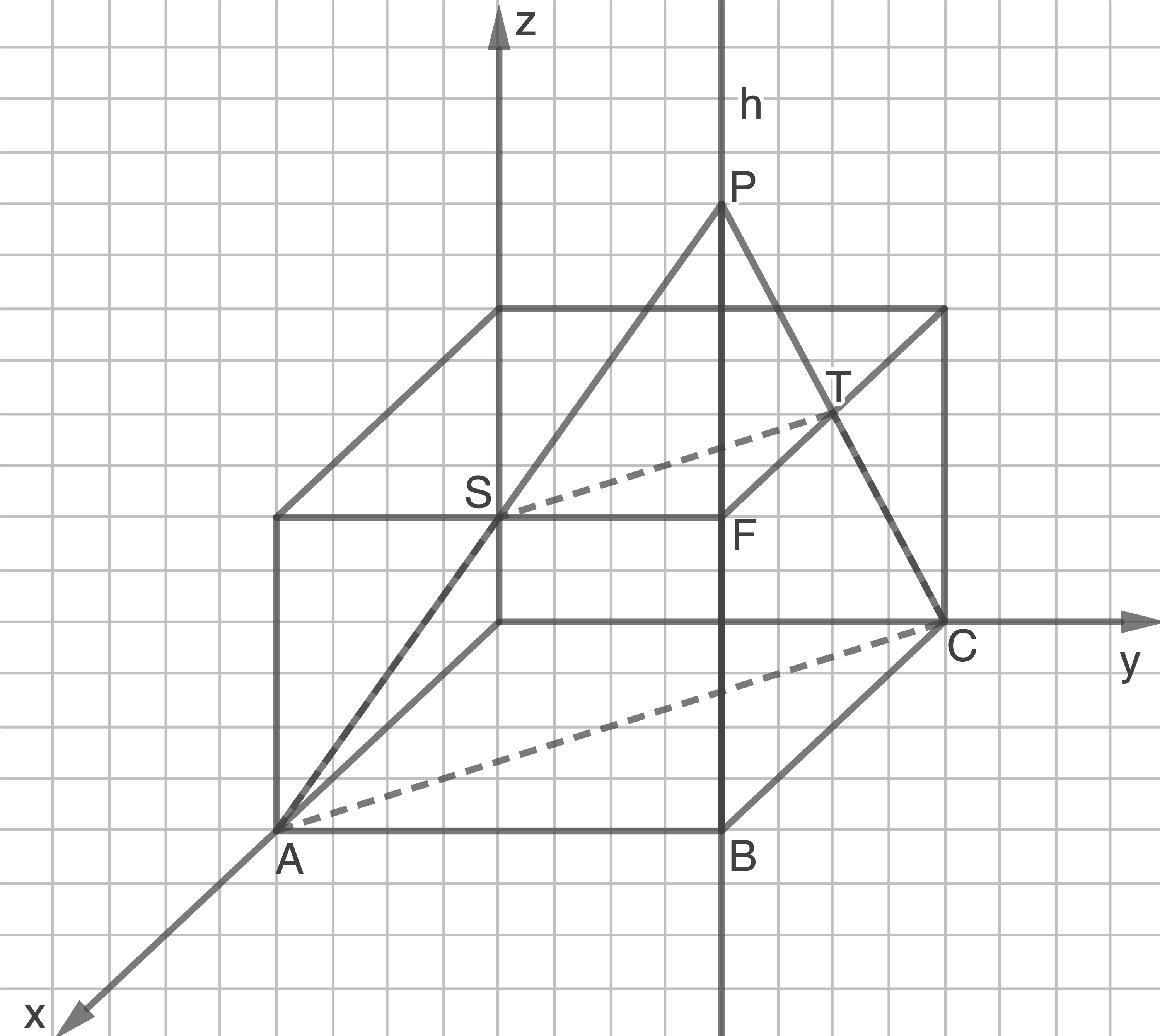
Beschreibe, wie man mithilfe der Abbildung ermitteln kann, dass die z-Koordinate 6 hat.
d)
Berechne das Volumen desjenigen der beiden Teilkörper, zu dem der Punkt 
gehört, und erläutere dein Vorgehen.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Alle Seitenflächen eines Quaders sind Rechtecke oder Quadrate. Da 
und Eckpunkte einer gemeinsamen Seitenfläche des Quaders und 
und 
zwei der Kanten sind, muss das Dreieck im Punkt einen rechten Winkel besitzen.
Die Länge der Seite ergibt sich mithilfe des zugehörigen Verbindungsvektors und seinem Betrag zu:
![\(\begin{array}[t]{rll}
\left|\overrightarrow{AB} \right|&=& \left|\pmatrix{4-4\\4-0\\0-0} \right| \\[5pt]
&=& \left|\pmatrix{0\\4\\0} \right| \\[5pt]
&=& \sqrt{0^2+4^2+0^2} \\[5pt]
&=& 4
\end{array}\)](https://mathjax.schullv.de/9d77755d8997e3049de09a6a504739b19c02eb6407171ba6a2b015efe245520e?color=5a5a5a)
Für die Länge von gilt analog:
![\(\begin{array}[t]{rll}
\left|\overrightarrow{BC} \right|&=& \left|\pmatrix{0-4\\4-4\\0-0} \right| \\[5pt]
&=& \left|\pmatrix{-4\\0\\0} \right| \\[5pt]
&=& \sqrt{(-4)^2+0^2+0^2} \\[5pt]
&=& 4
\end{array}\)](https://mathjax.schullv.de/2de66cfaa67dfdd50982805d1bd70e77726ee5bb39388e3bd78a86b3063b980e?color=5a5a5a)
Das Dreieck ist also gleichschenklig.
Aufgrund des rechten Winkels ergibt sich der Flächeninhalt zu:
![\(\begin{array}[t]{rll}
A_{ABC}&=& \dfrac{1}{2}\cdot 4\cdot 4 \\[5pt]
&=& 8
\end{array}\)](https://mathjax.schullv.de/8fddde265f138fe257956be0918c7699e29a8c95bfed4523a9ecac5a0e146597?color=5a5a5a)
Das Dreieck hat einen Flächeninhalt von 8 FE.
Die Länge der Seite
b)
c)
d)
