Teil B – Pflichtaufgaben

Aufgabe 1

Die Grafik zeigt die Veränderung der Nutzung von Medien in Deutschland. Es wird die durchschnittliche tägliche Nutzung durch die gesamte Bevölkerung in Minuten angegeben.

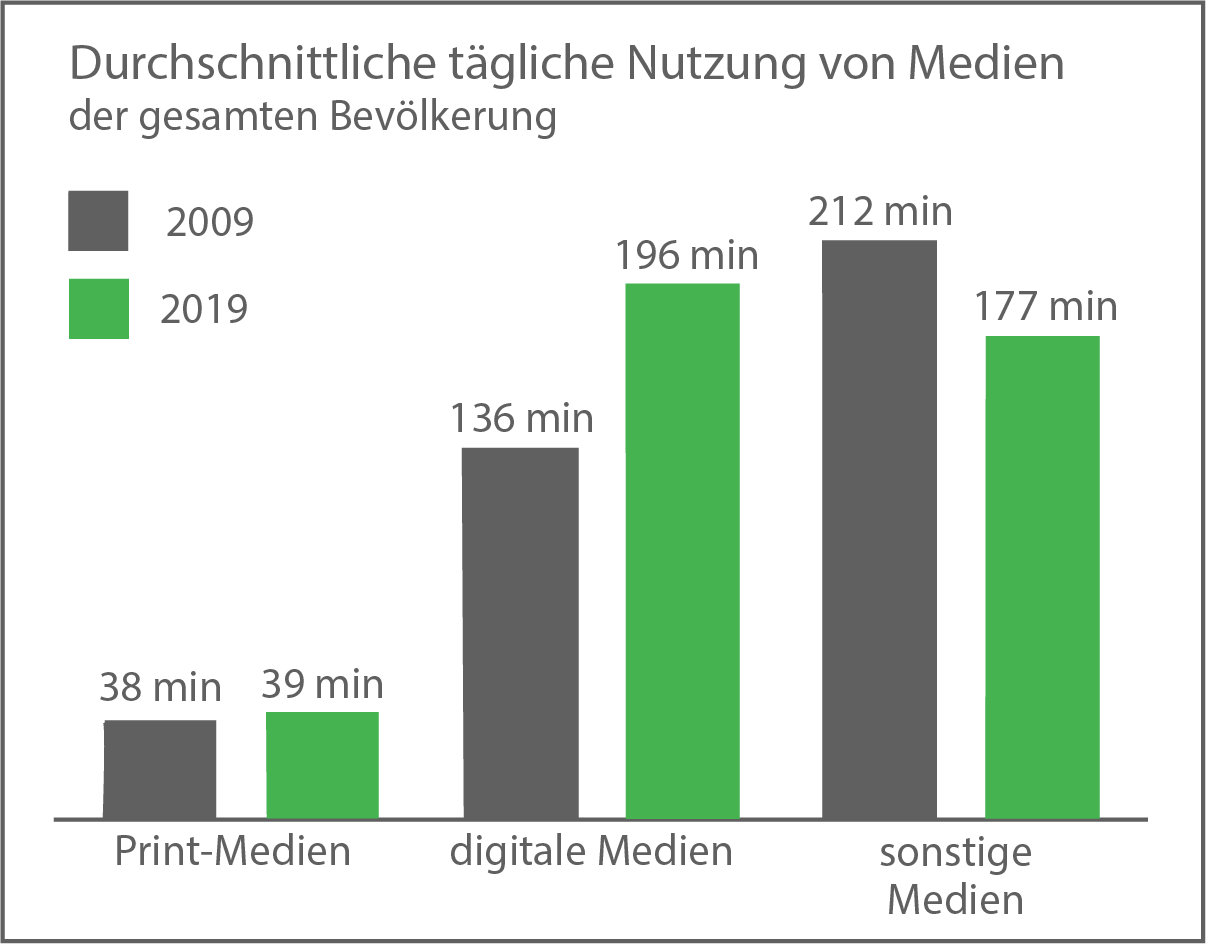
Balkendiagramm zur täglichen Mediennutzung der Bevölkerung in 2009 und 2019.

Berechne für 2009 den prozentualen Anteil der Nutzung von Print-Medien an der gesamten Mediennutzung.

Berechne, um wie viel Prozent die Nutzung der digitalen Medien 2019 gegenüber 2009 stieg.

Für das Jahr 2023 wurden die folgenden Daten veröffentlicht.

Im Durchschnitt spielten Jugendliche täglich $34$ Minuten online. Das entsprach $13,2\,\text{%}$ der täglichen Nutzung digitaler Medien durch Jugendliche.

Berechne, wie viel Minuten Jugendliche täglich digitale Medien im Durchschnitt nutzten.

(6 BE)

Aufgabe 2

Der Graph einer linearen Funktion $f$ verläuft durch den Punkt $A( 0\mid– 6 )$ und hat die Nullstelle $x_0 = 4.$

Zeichne den Graphen der Funktion $f$ in ein rechtwinkliges Koordinatensystem mindestens im Intervall $–1\leq x \leq 5.$

Gib die Funktionsgleichung der Funktion $f$ an.

Der Graph $f$ schneidet die $x$ -Achse im Punkt $B.$ Der Koordinatenursprung ist Punkt $C.$
Die Punkte $A, B$ und $C$ bilden das Dreieck $ABC.$
Eine Längeneinheit im Koordinatensystem entspricht $1,0\;\text{cm}.$

Berechne die Länge der Strecke $AB.$

Gib den Flächeninhalt des Dreiecks $ABC$ an.

(6 BE)

Aufgabe 3

In einer Stadt wurde ein zylinderförmiges Wasserbecken mit Steinrand und einem ringförmigen Sandweg angelegt (siehe Abbildung).

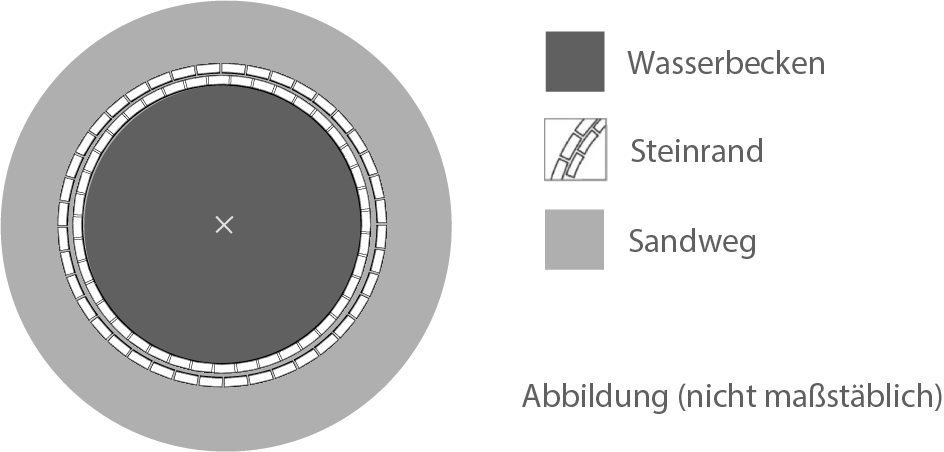
Diagramm eines Wasserbeckens mit Steinrand und Sandweg, nicht maßstäblich.

Das Wasserbecken hat einen Durchmesser von $14,00\;\text{m}.$ Der Steinrand ist $50\;\text{cm}$ breit.
Die Breite des Sandweges beträgt $3,50\;\text{m}.$

Das Wasserbecken muss im Frühjahr neu gefüllt werden.
Die Wasserhöhe beträgt $0,30\;\text{m}.$

Berechne, wie viel Liter Wasser dafür benötigt werden.

Berechne den äußeren Umfang des Steinrandes.

Berechne den Flächeninhalt des Sandweges.

(6 BE)

Aufgabe 4

Im Rahmen der „Europäischen Gradmessung 1864“ wurde auch das Königreich Sachsen vermessen. Dazu wurden unter anderem diese vier Messpunkte festgelegt (siehe Abbildung).

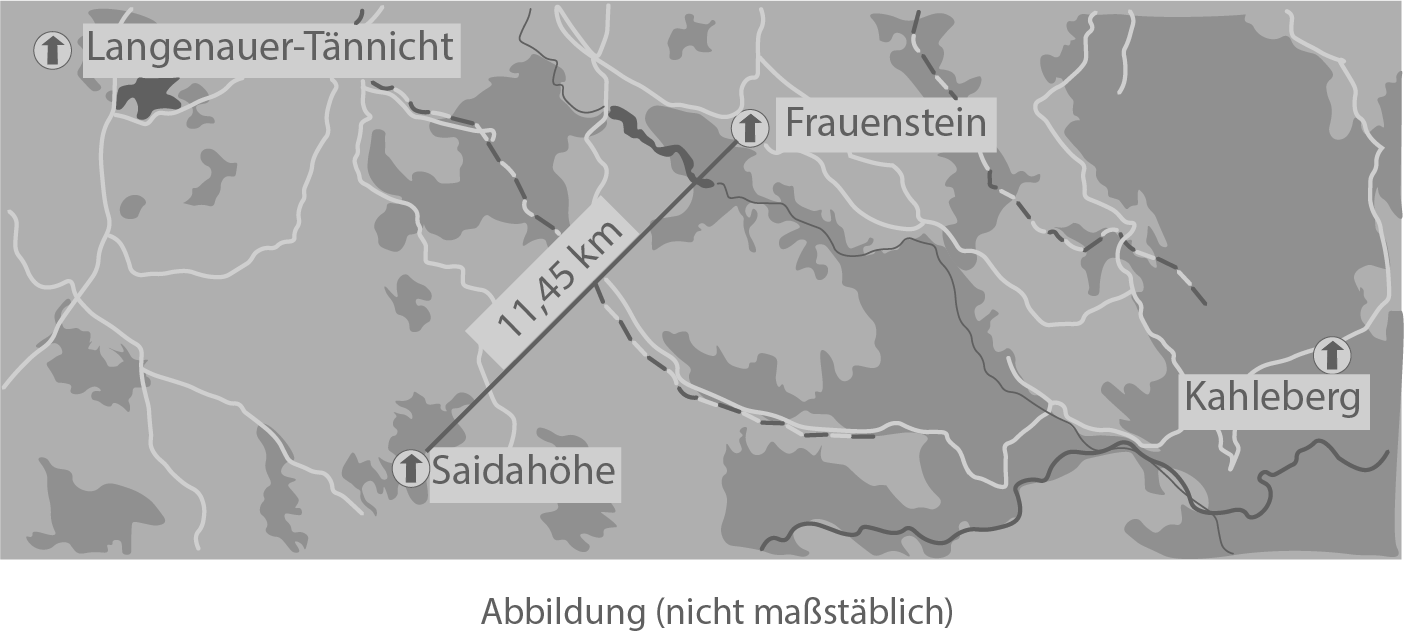
Karte mit markierten Orten und einer Strecke von 11,45 km, nicht maßstabsgetreu.

Die weitere Vermessung erfolgte mittels Winkelmessungen und Berechnungen von Längen in Dreiecken.

Im Erzgebirge wurde der Messpunkt Kahleberg $(K)$ von den Messpunkten Saidahöhe $(S)$ und Frauenstein $(F)$ angepeilt (siehe Abbildung). Die Messpunkte $S, K$ und $F$ bilden das Dreieck $SKF.$

Für das Dreieck $SKF$ erhielt man die folgenden Winkelgrößen.

$\sphericalangle KSF=37,9^\circ$
$\sphericalangle SFK=113,7^\circ$

Zeichne das Dreieck $SKF$ im Maßstab 1 : 200 000.

Berechne die Entfernung des Messpunktes Saidahöhe $(S)$ vom Messpunkt Kahleberg $(K).$

Der Messpunkt Langenauer-Tännicht $(L)$ ist vom Messpunkt Saidahöhe $(S)$ $12,84\;\text{km}$ und vom Messpunkt Frauenstein $(F)$ $16,55\;\text{km}$ entfernt. Diese Messpunkte bilden das Dreieck $LSF.$

Berechne die Größe des Winkels $\sphericalangle SLF.$

(6 BE)

Aufgabe 5

Gegeben ist das folgende Zahlenrätsel.

Vermindert man das Zehnfache der gesuchten Zahl um acht, so erhält man die Summe aus dem Zwölffachen der gesuchten Zahl und vier.

Stelle eine Gleichung auf.

Gib die gesuchte Zahl an.

Berechne die Nullstellen der folgenden quadratischen Funktion.

$y=f(x)=x^2-8x+7$

Das Volumen einer Pyramide beträgt $80,0\;\text{cm}^3.$ Die quadratische Grundfläche der Pyramide hat eine Seitenlänge von $5,0\;\text{cm}.$
Berechne die Höhe dieser Pyramide.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

Prozentualer Anteil der Print-Medien an der gesamten Mediennutzung 2009:
Gesamtnutzung 2009: $38\;\text{min}+136\;\text{min}+212\;\text{min}=386\;\text{min}$
Anteil Print: $\frac{38}{386}\cdot 100\approx 9,85\,\text{%}$

Der prozentuale Anteil der Print-Medien beträgt etwa $9,85\,\text{%}.$

Prozentuale Steigung der Nutzung der digitalen Medien 2019 gegenüber 2009:
Zuwachs: $196\;\text{min}-136\;\text{min}=60\;\text{min}$
$\frac{60}{136}\cdot 100\approx 44,12\,\text{%}$

Die Nutzung der digitalen Medien 2019 gegenüber 2009 stieg um etwa $44,12\,\text{%}.$

Durchschnittliche tägliche digitale Medien Nutzung von Jugendlichen:
$34\;\text{min} :0,132\approx 257,58\;\text{min}$

Die durchschnittliche tägliche digitale Medien Nutzung von Jugendlichen beträgt etwa $257,58\;\text{Minuten}.$

Lösung 2

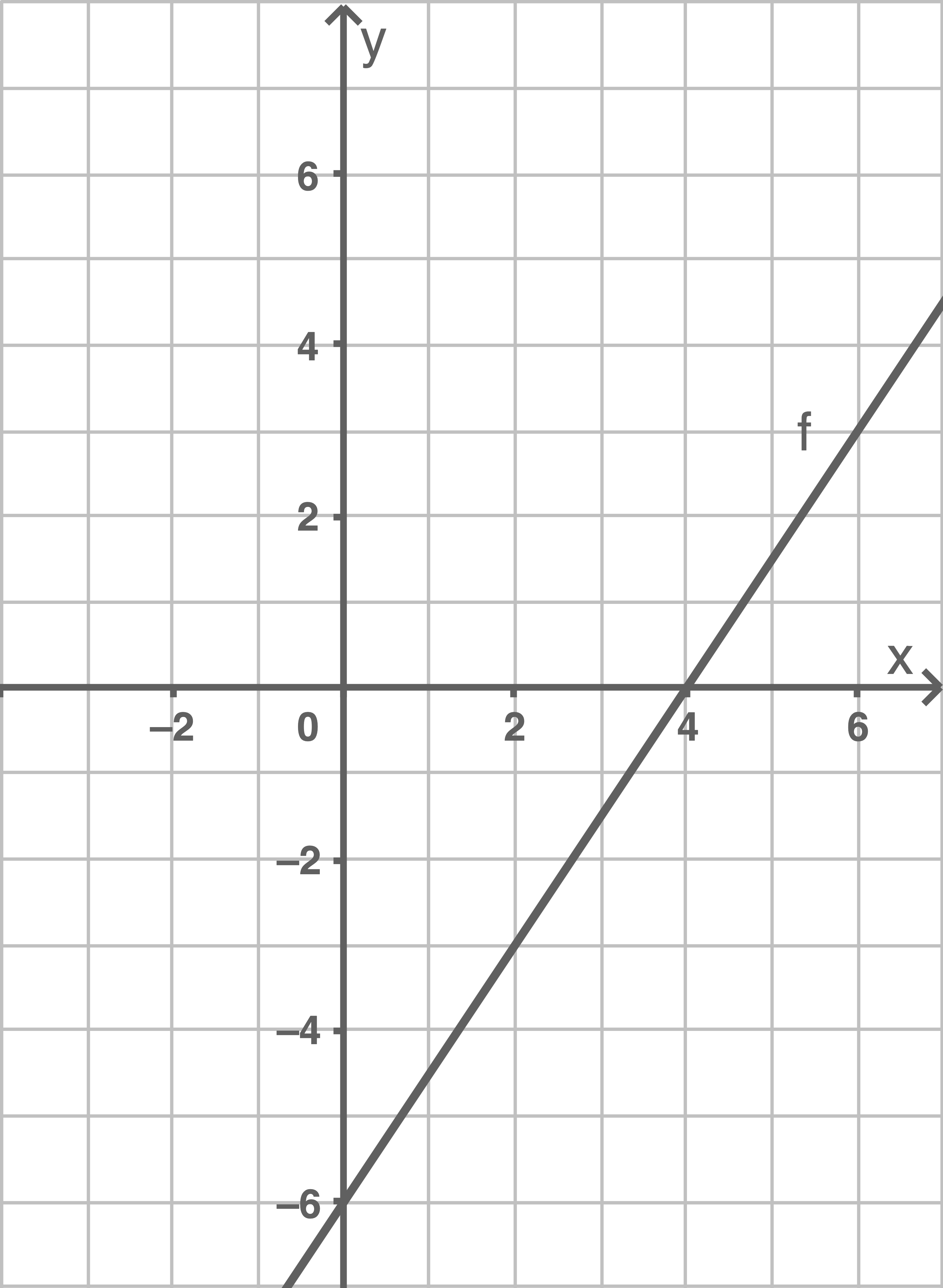
Graph eines linearen Funktion mit Achsenbeschriftungen und einem Anstieg.

Allgemeine Funktionsgleichung: $f(x)=m\cdot x+c$
Bestimme die Steigung $m:$ $m=\frac{y_2-y_1}{x_2-x_1}=\frac{0-(-6)}{4-0}=\frac{3}{2}$
Bestimme den y-Achsenabschnitt $c:$ $c$ ist gegeben durch den Punkt $A(0\mid -6),$ da der Graph die $y-$ Achse bei $-6$ schneidet.

Daraus ergibt sich folgende Funktionsgleichung: $f(x)=\frac{3}{2}x-6$

Länge der Strecke $\overline{AB}$ berechnen:
$\overline{AB}=\sqrt{(4-0)^2+(0-(-6))^2}=\sqrt52\approx 7,21\;\text{cm}$
Die Länge der Strecke $\overline{AB}$ beträgt etwa $7,21\;\text{cm}.$

Flächeninhalt des Dreiecks $ABC$ berechnen:
$A=\dfrac{1}{2}\cdot AC\cdot CB=\dfrac{1}{2}\cdot 6\cdot 4=12\;\text{cm}^2$
Der Flächeninhalt des Dreiecks $ABC$ beträgt $12\;\text{cm}^2$

Lösung 3

Benötigte Wassermenge (Liter):

$\begin{array}[t]{rlll} V&=&\pi\cdot r^2\cdot h \\[5pt] &=&\pi\cdot 7^2\cdot 0,3 \\[5pt] &\approx& 46,18\;\text{m}^3 \end{array}$

Umrechnung in Liter:

$\begin{array}[t]{rlll} 1\;\text{m}^3&=&1000\;\text{l} \\[5pt] V&\approx&46\, 180\;\text{l} \end{array}$

Für das Wasserbecken werden etwa $46\, 180$ Liter Wasser benötigt.

Äußerer Umfang des Steinrandes:
Äußeres Radius des Steinrandes: $r=7\;\text{m}+0,5\;\text{m}=7,5\;\text{m}$
$U=2\pi r= 2\cdot \pi \cdot 7,5\;\text{m} \approx 47,12\;\text{m}$

Der äußere Umfang des Steinrandes beträgt etwa $47,12\;\text{m}.$

Flächeninhalt des Sandweges berechnen:
Äußerer Radius Sandweg: $r=7,5\;\text{m}+3,5\;\text{m}=11\;\text{m}$
Innerer Radius Sandweg $=$ äußerer Radius Steinrand $r=7,5\;\text{m}$
$A=\pi(11^2-7,5^2)\approx 203,42\;\text{m}^2$

Der Flächeninhalt des Sandweges beträgt etwa $203,42\;\text{m}^2.$

Lösung 4

Fehlenden Winkel bestimmen: $\sphericalangle SKF=180^\circ-37,9^\circ -113,7^\circ=28,4^\circ$

Dreieck $SKF$ im Maßstab 1 : 200 000, d.h. $1\;\text{cm}$ auf der Zeichnung entspricht $2\;\text{km}$ in der Realität.

$\overline{SF}=11,45\;\text{km}=11\, 450\;\text{m}$
$\frac{11\, 450\;\text{m}}{200\, 000}=0,05725\;\text{m}=5,725\;\text{cm}$

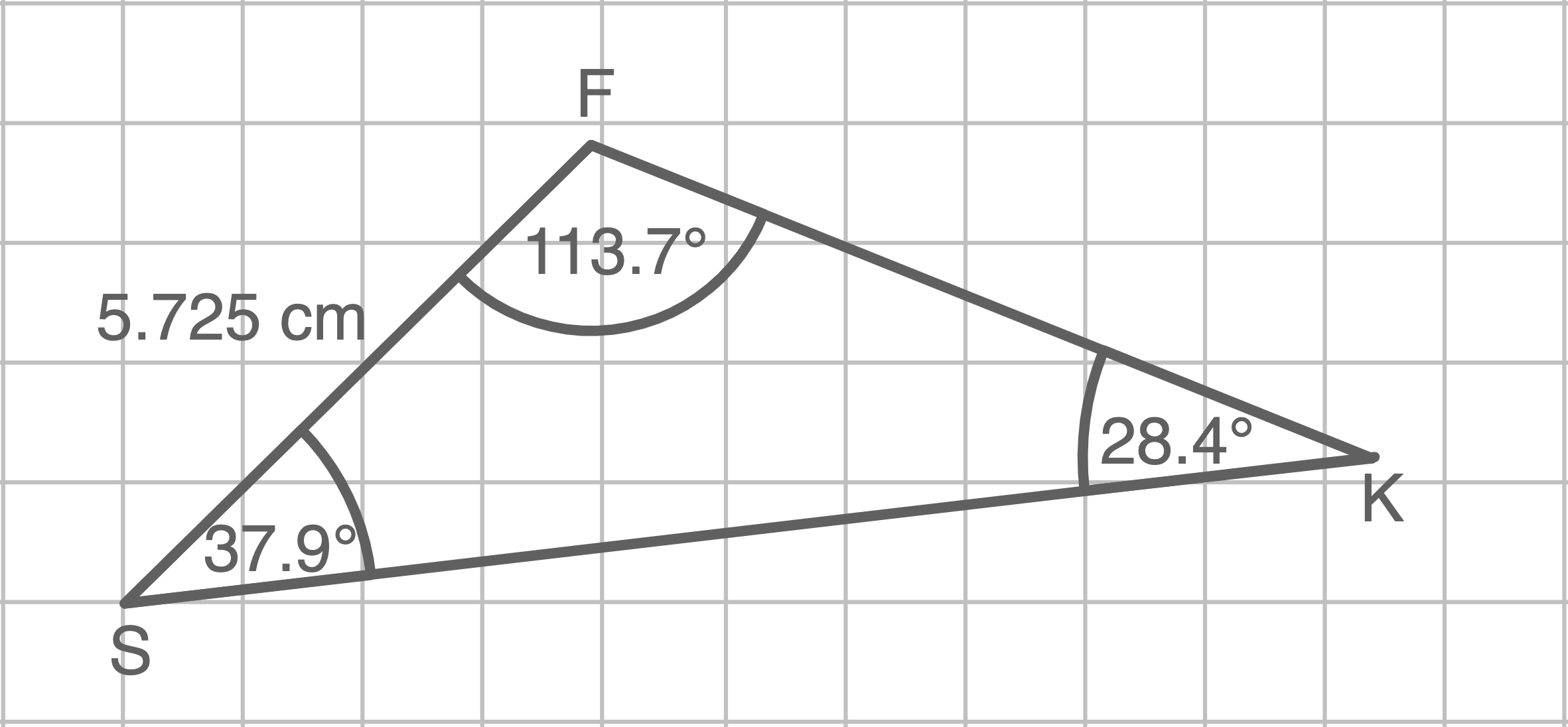
Geometrisches Diagramm eines Dreiecks mit Seitenlängen und Winkeln.

Entfernung des Messpunktes Saidahöhe $(S)$ vom Messpunkt Kahleberg $(K)$ mit dem Sinussatz berechnen:
$\frac{KF}{\sin (\sphericalangle KSF)}=\frac{SK}{\sin (\sphericalangle SFK)}$
$\frac{11,45\;\text{km}}{\sin (37,9^\circ)}=\frac{SK}{\sin (113,7^\circ)}$
$SK=11,45\cdot \frac{\sin (113,7^\circ)}{\sin (37,9^\circ)}\approx 11,45\cdot 2,84\approx 32,52\;\text{km}$

Entfernung des Messpunktes Saidahöhe $(S)$ vom Messpunkt Kahleberg $(K)$ beträgt etwa $32,52\;\text{km}.$

Winkel $\sphericalangle SLF$ im Dreieck $LSF$ mit dem Kosinussatz bestimmen:
$\cos (\sphericalangle SLF)=\frac{LS^2+LF^2-SF^2}{2\cdot LS\cdot LF}=\frac{12,84^2+16,55^2-11,45^2}{2\cdot 12,84\cdot 16,55}\approx0,72$
$\sphericalangle SLF= \cos(0,72)\approx 43,95^\circ$

Lösung 5

Gleichung aufstellen:
$\begin{array}[t]{rlll} 10x-8&=&12x+4 &\mid\;+8 \\[5pt] 10x&=&12x+12 &\mid\;-12x\\[5pt] -2x&=&12 &\mid\;:(-2)\\[5pt] x&=&-6 \end{array}$

Die gesuchte Zahl ist $-6.$

Nullstellen mit der Mitternachtsformel berechne:

$f(x)=x^2-8x+7=0$
$x_{1,2}=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\begin{array}[t]{rll} x_{1,2}&=&\dfrac{-(-8)\pm \sqrt{(-8)^2-4\cdot 1\cdot 7}}{2\cdot 1} \\[5pt] x_{1,2}&=&\dfrac{8\pm \sqrt{36}}{2} \\[5pt] x_{1,2}&=&\dfrac{8\pm 6}{2} \\[5pt] x_1&=&1 \\[5pt] x_2&=&7 \end{array}$

Höhe der Pyramide berechnen:
$A=a^2=(5\;\text{cm})^2=25\;\text{cm}^2$
$h=\frac{3V}{A}=\frac{3\cdot 80\;\text{cm}^3}{25\;\text{cm}^2}=9,6\;\text{cm}$

Die Höhe der Pyramide beträgt $9,6\;\text{cm}.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?