Teil A – Arbeitsblatt

$19,04\cdot 2,7=$

$\dfrac{10-6}{-18+5}=$

$4^x=64\qquad$ $x=$

$\frac{2}{5}$ von $45\;\text{min}$ sind $\text{____________} \;\text{min}.$

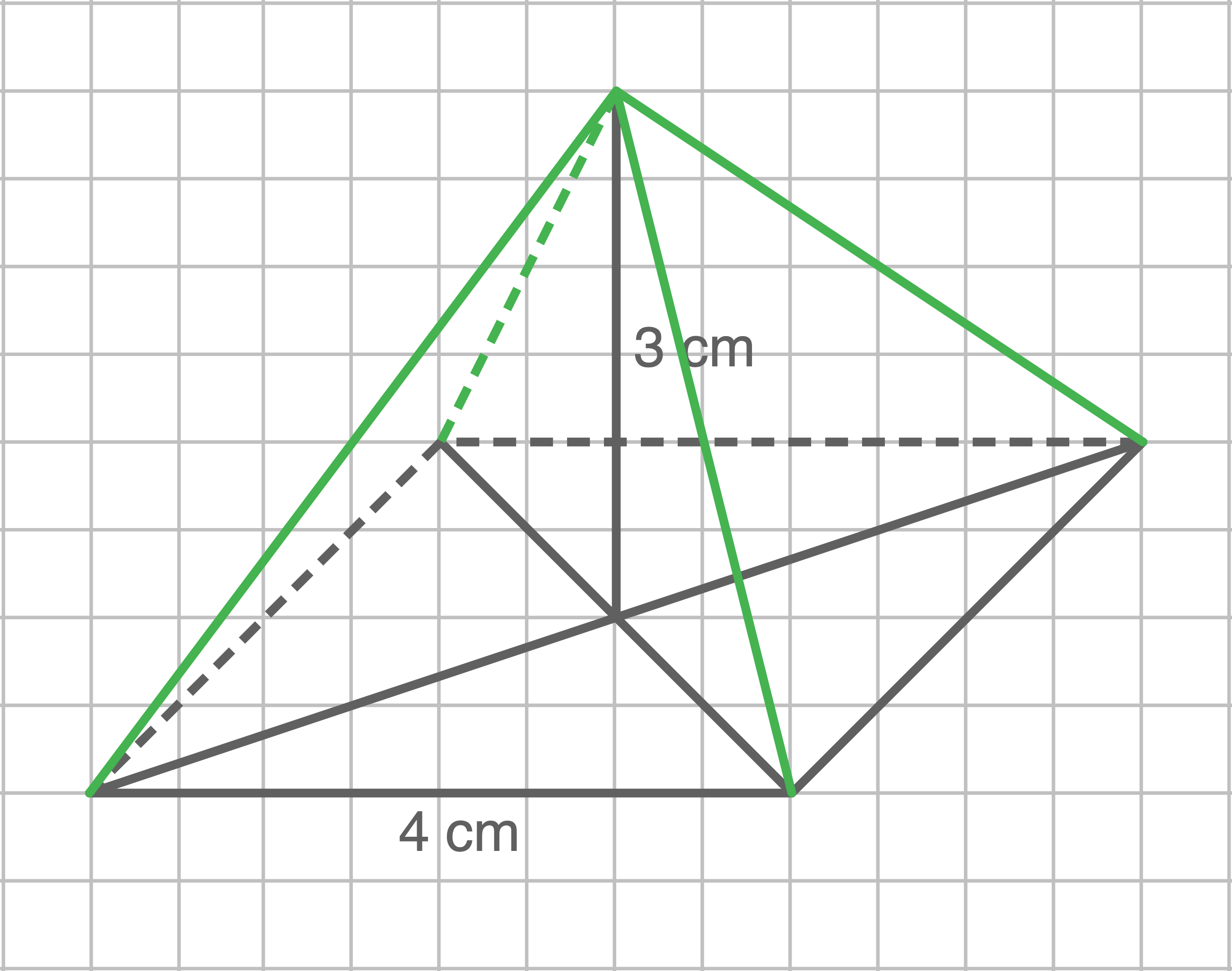
Eine $3,0\;\text{cm}$ hohe Pyramide hat eine quadratische Grundfläche mit der Seitenlänge $a=4,0\;\text{cm}.$

Zeichne ein Schrägbild dieser Pyramide.

Wahr oder falsch? Kreuze an.

	wahr	falsch
Die kleinste ganze Zahl ist $-1.$		
Ein Dreieck mit den Seitenlängen $3\;\text{cm},$ $4\;\text{cm}$ und $5\;\text{cm}$ ist rechtwinklig.		

Notiere den Messwert.

$\text{____________}$ $\text{ml}$

Messbecher mit Skala, zeigt Flüssigkeitsstand zwischen 20 und 60 ml.

Gib den Zentralwert der Temperaturen an.

$19^\circ C \quad 13^\circ C \quad 12^\circ C \quad 16^\circ C \quad 12^\circ C \quad 10^\circ C \quad 14^\circ C$

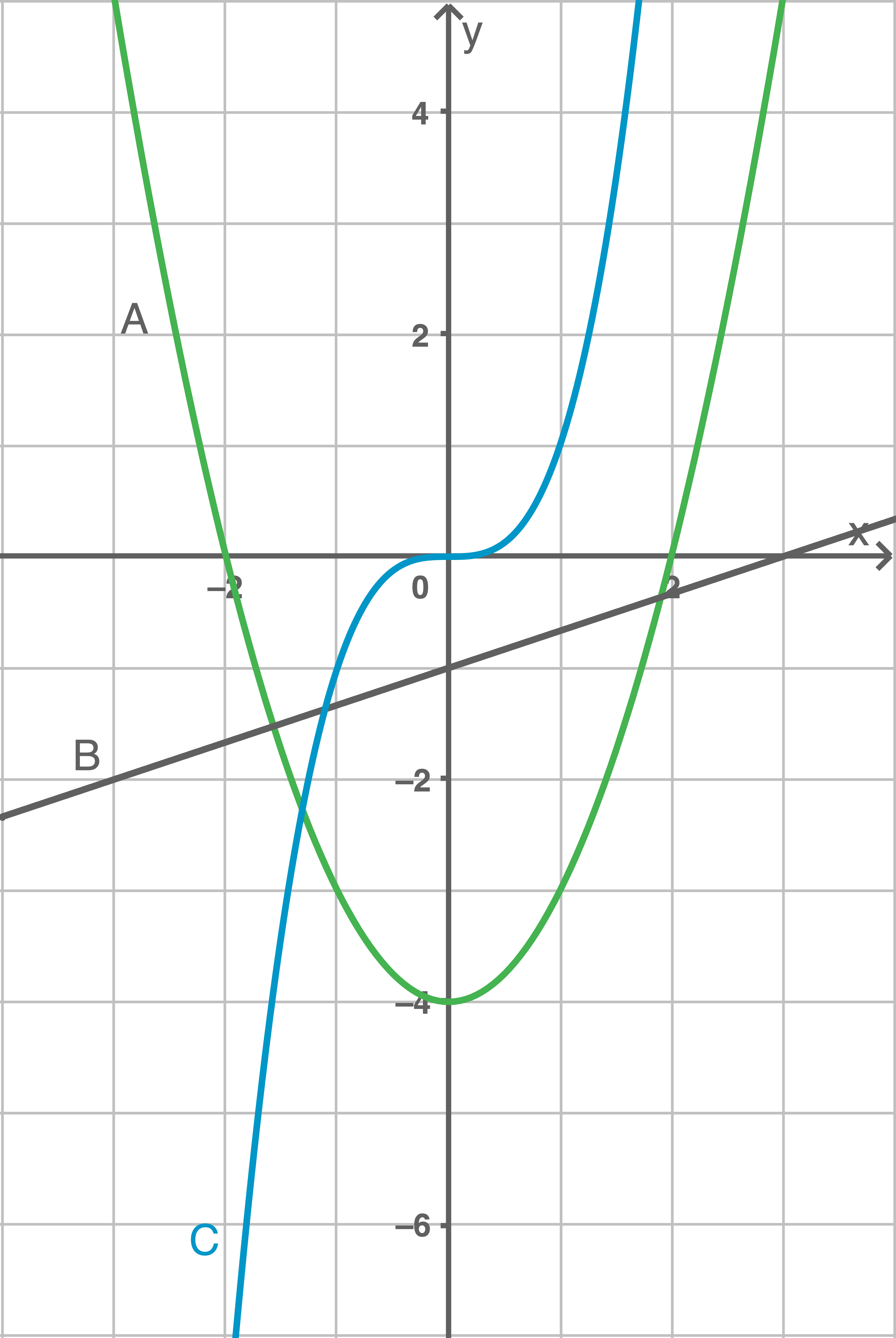
Ordne jeder Funktionsgleichung genau einen Graphen zu.

Funktionsgleichung	Graph
$y=f(x)=\dfrac{1}{3}x-1$
$y=x^2-4$
$y=x^3$

Koordinatensystem mit x- und y-Achse, grüne Parabel, blaue Kurve, graue Gerade und Beschriftungen A, B, C

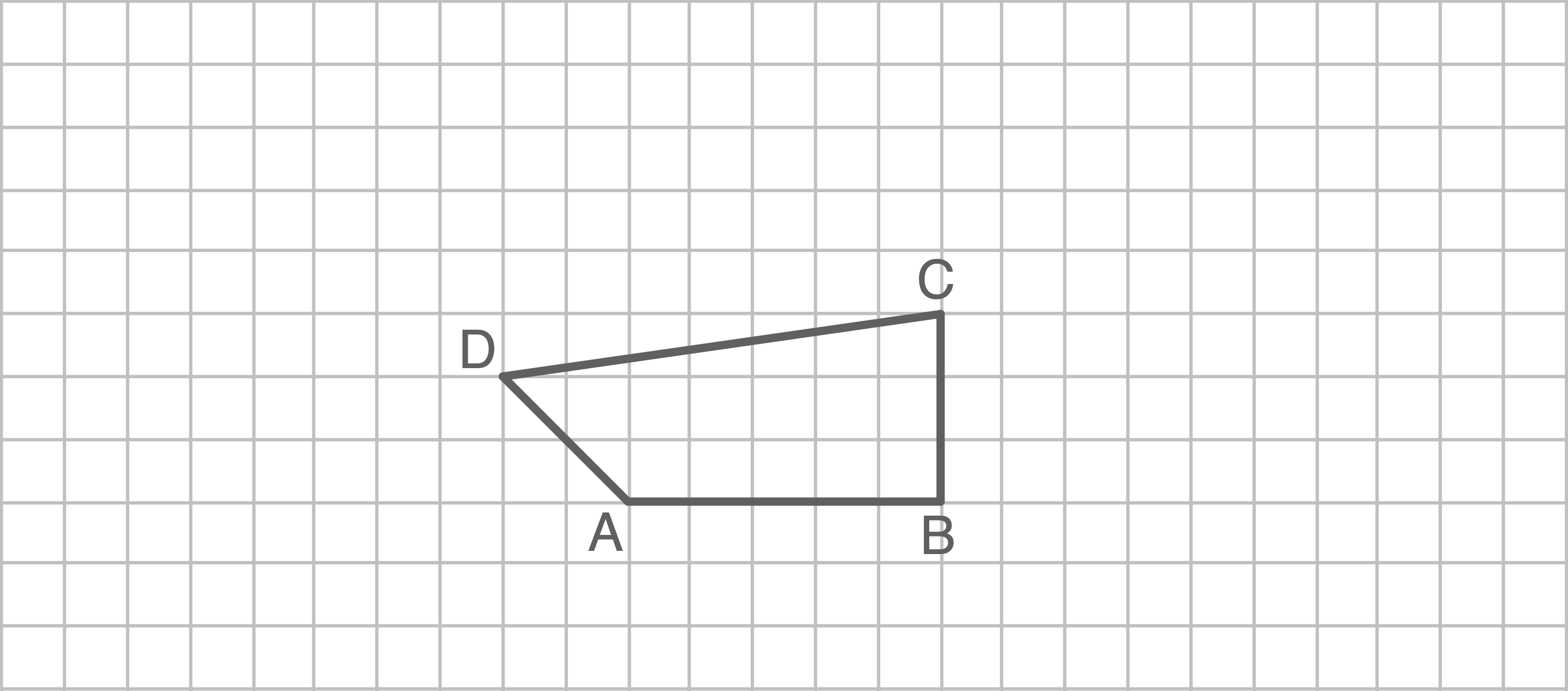
Zeichne ein Bild $A_1B_1C_1D_1$ des Vierecks $ABCD$ im Maßstab 3 : 1.

Geometrische Darstellung eines Trapezes mit den Punkten A, B, C und D auf einem Gitterhintergrund.

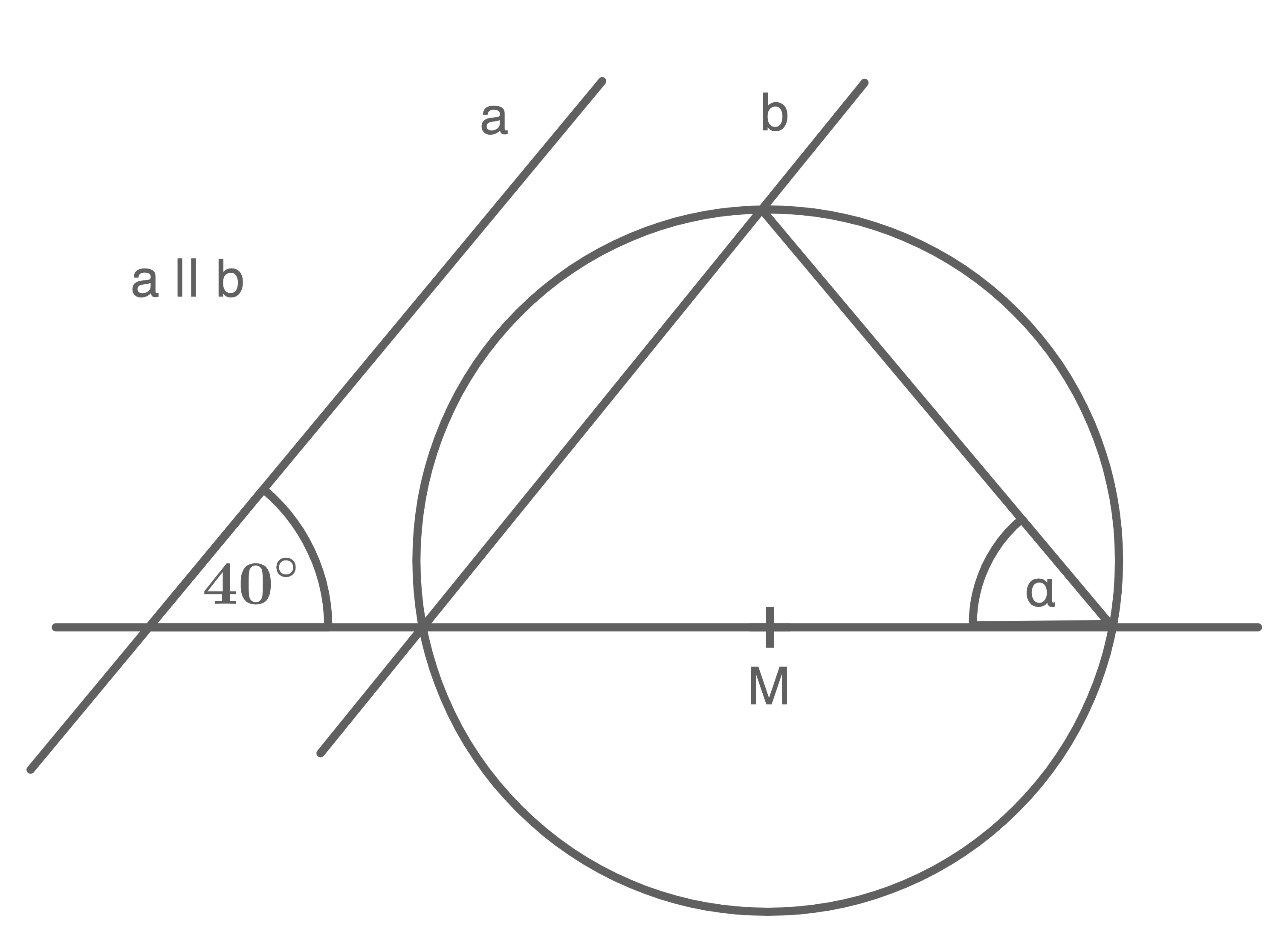
Gib die Größe des Winkels $\alpha$ an.

Diagramm mit parallelen Linien, einem Kreis und verschiedenen Winkeln.

Abbildung (nicht maßstäblich)

Ersetze die Symbole so durch Ziffern, dass eine wahre Aussage entsteht.
Gleiche Symbole bedeuten gleiche Ziffern.

Mathematische Gleichung mit Symbolen für Kartenfarben: Kreuz, Herz und Diamant.

(12 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$19,04\cdot 2,7=51,408$

$\dfrac{10-6}{-18+5}=-\dfrac{4}{13}$

$4^x=64\qquad$ $x=3$

$\frac{2}{5}$ von $45\;\text{min}$ sind $18\;\text{min}.$

Geometrische Zeichnung mit einem 4 cm langen und einem 3 cm hohen Dreieck auf einem karierten Hintergrund.

	wahr	falsch
Die kleinste ganze Zahl ist $-1.$		
Ein Dreieck mit den Seitenlängen $3\;\text{cm},$ $4\;\text{cm}$ und $5\;\text{cm}$ ist rechtwinklig.		

Erläuterung:
Die 1. Aussage ist falsch, denn es gibt keine kleinste ganze Zahl.
Die 2. Aussage ist wahr, denn es gilt:

$(3\; \text{cm})^2 + (4\; \text{cm})^2 = 9\; \text{cm}^2 + 16; \text{cm}^2 = 25\; \text{cm}^2 = (5\, \text{cm})^2$

Nach der Umkehrung des Satzes des Pythagoras ist das Dreieck rechtwinklig.

Messwert: $44\;\text{ml}$

Temperaturen sortiert: $10^\circ \quad 12^\circ C \quad 12^\circ C \quad 13^\circ C \quad 14^\circ C \quad 16^\circ C \quad 19^\circ C$

Der zentrale Wert in einer geordneten Liste mit ungerader Anzahl an Werten ist derjenige, der genau in der Mitte liegt.
Der zentrale Wert ist hier $13^\circ C.$

Funktionsgleichung	Graph
$y=f(x)=\dfrac{1}{3}x-1$	B
$y=x^2-4$	A
$y=x^3$	C

Erläuterung:
Die 1. Funktionsgleichung ist eine lineare Funktion. Ihr Graph ist eine Gerade mit der Steigung $m = \tfrac{1}{3}$ und dem $y$ -Achsenabschnitt $b = -1$ .
Die 2. Funktionsgleichung ist eine quadratische Funktion. Ihr Graph ist eine nach nach oben geöffnete Normalparabel, die um $4$ Einheiten nach unten verschoben ist.
Die 3. Funktionsgleichung ist eine Potenzfunktion 3. Grades. Ihr Graph verläuft durch den Koordinatenursprung und ist punktsymmetrisch zu diesem.

Geometrisches Diagramm mit Linien und Punkten A, B, C und D auf einem karierten Hintergrund.

$\alpha= 180^\circ - 40^\circ-90^\circ=50^\circ$

Erläuterung:
Da Stufenwinkel an geschnittenen Parallelen gleich groß sind, beträgt der von der horizontalen Geraden und der Geraden $b$ eingeschlossene Winkel ebenfalls $40^{\circ}.$ Nach dem Satz des Thales ist der Winkel am Punkt auf dem Kreisbogen ein rechter Winkel. Da die Innenwinkelsumme im Dreieck $180^{\circ}$ beträt, kann der fehlende Winkel anschließend berechnet werden.

Mathematische Gleichung mit Karten und Zahlen, die Addition darstellt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?