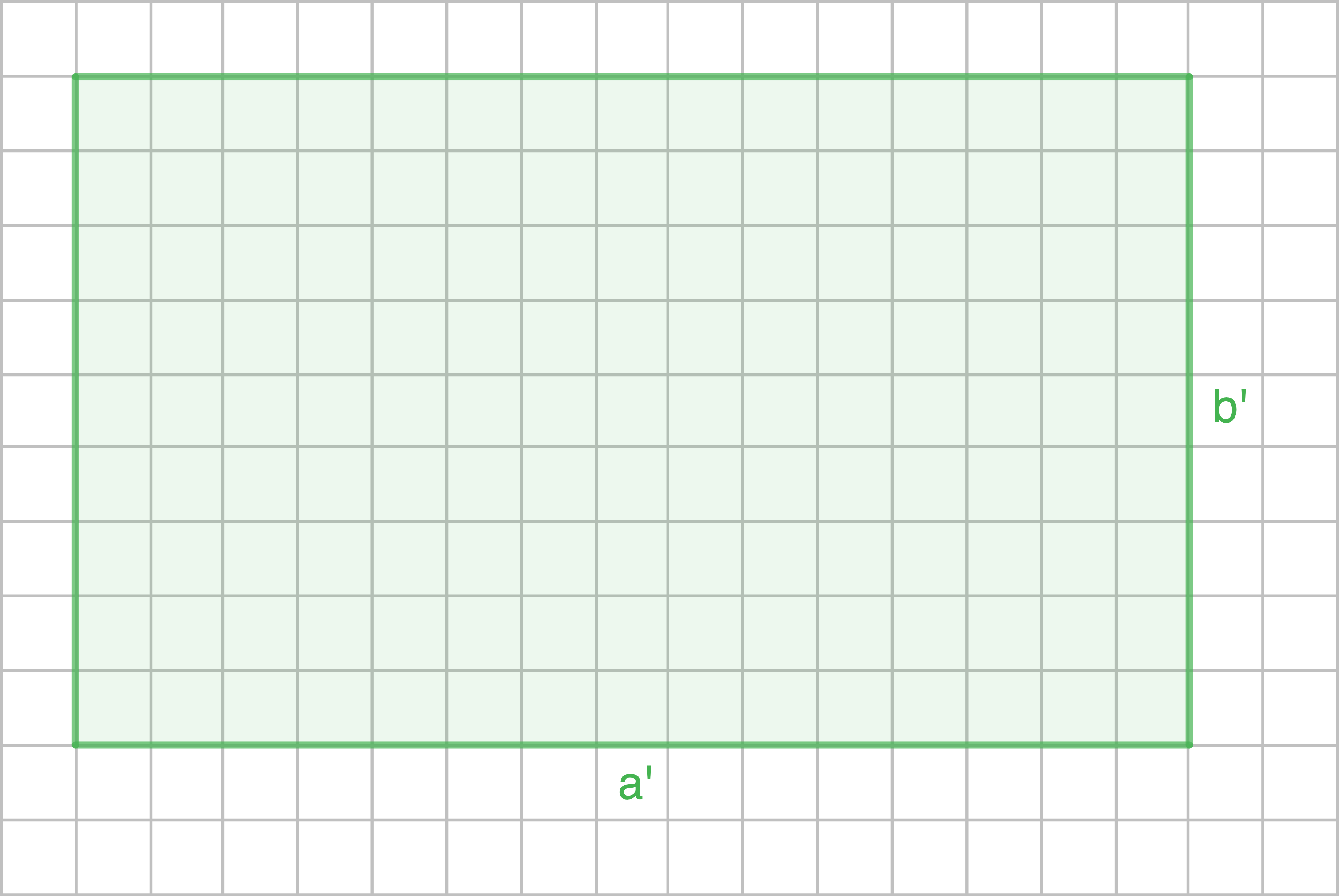
Ähnliche Figuren
Wird eine Figur vergrößert oder verkleinert, so entsteht eine neue Figur. Diese Figur wird ähnliche Figur genannt, wenn gilt:
Für 
ergibt sich eine Vergrößerung, für 
ergibt sich eine Verkleinerung.
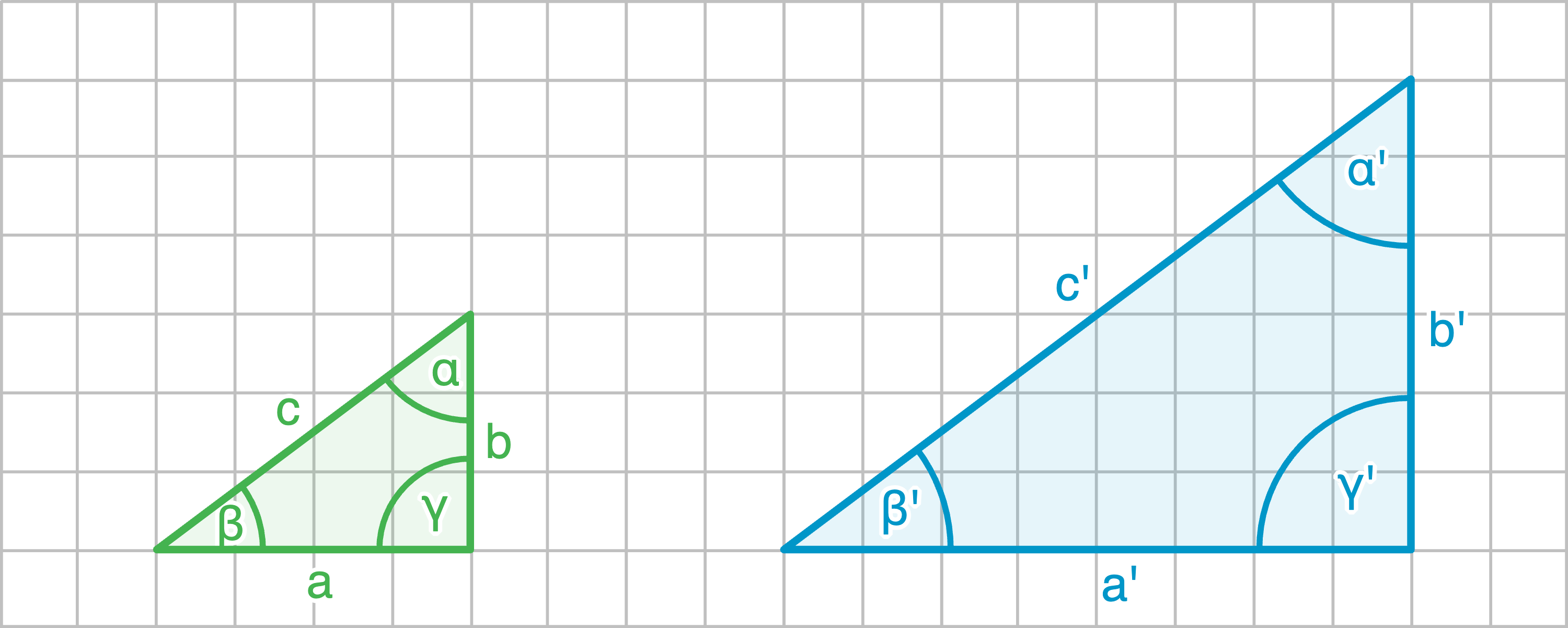
- Einander entsprechende Winkel sind gleich groß
- Einander entsprechende Seiten stehen im gleichen Längenverhältnis
zueinander. Dabei gilt:
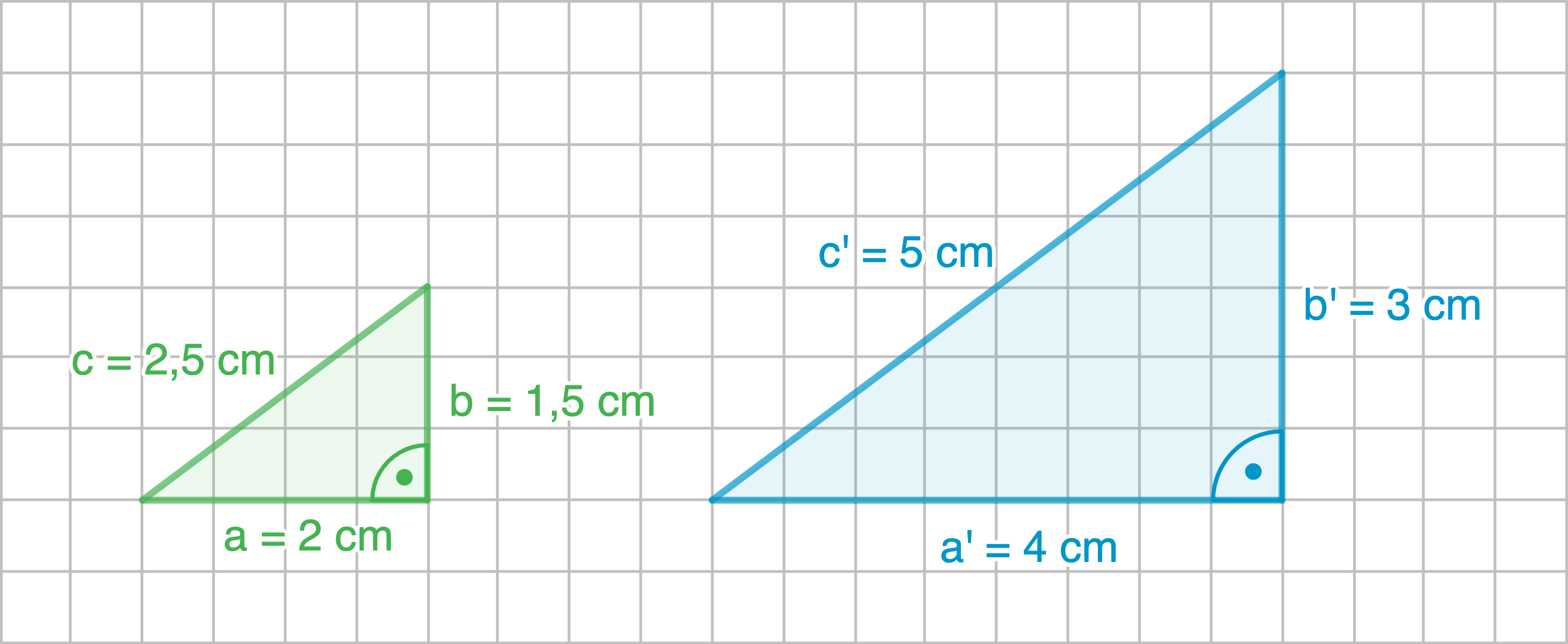
Beispiel
Längenverhältnisse überprüfen:
Somit gilt: 
Da die Längenverhältnisse aller zusammengehörenden Seiten gleich sind und alle Winkel gleich groß sind, sind die Dreiecke ähnlich.
1
Zeichne ähnliche Figuren mit dem angegebenen Vergrößerungsfaktor.
a)
Vergrößerungsfaktor: 
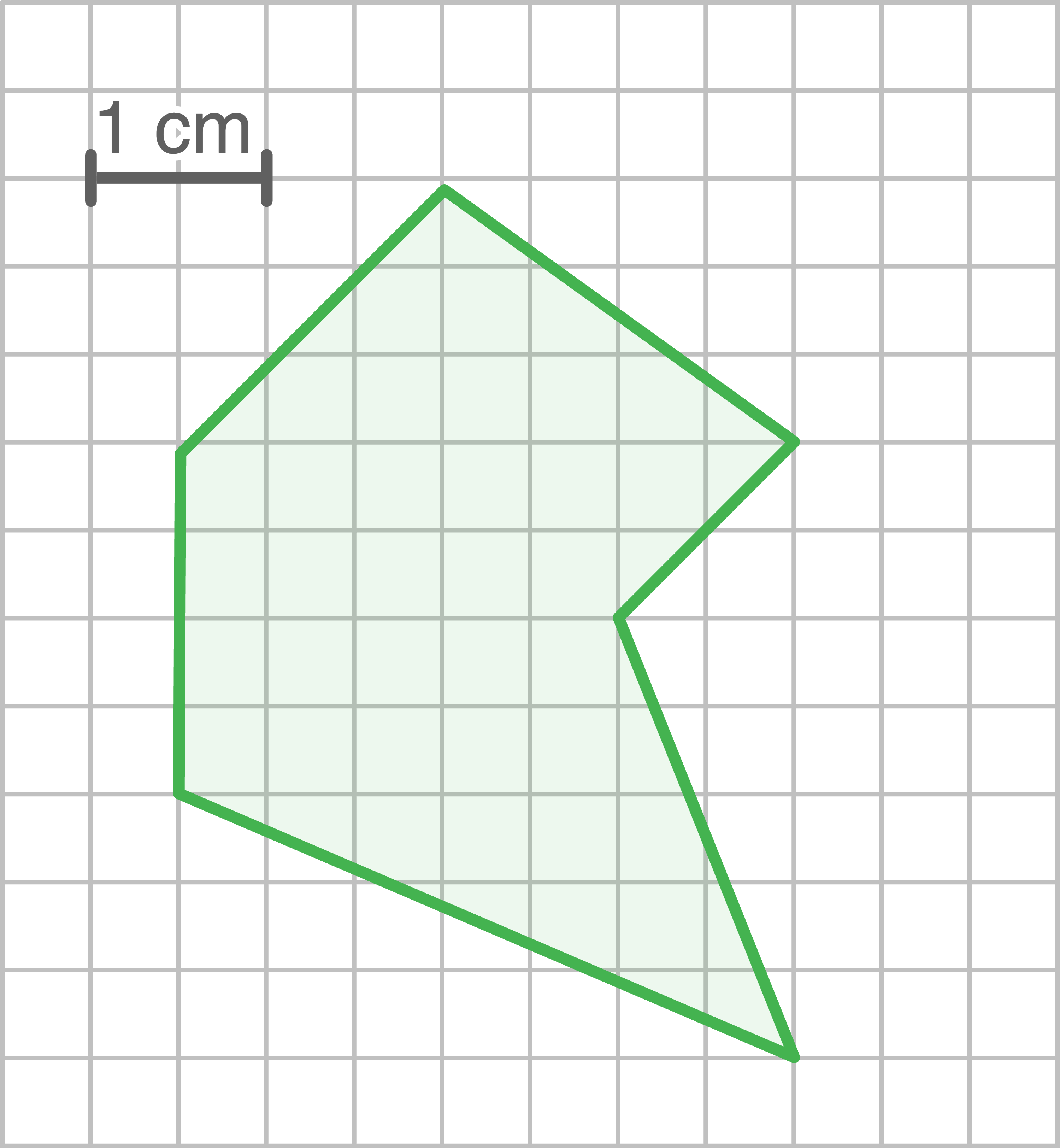
b)
Vergrößerungsfaktor: 
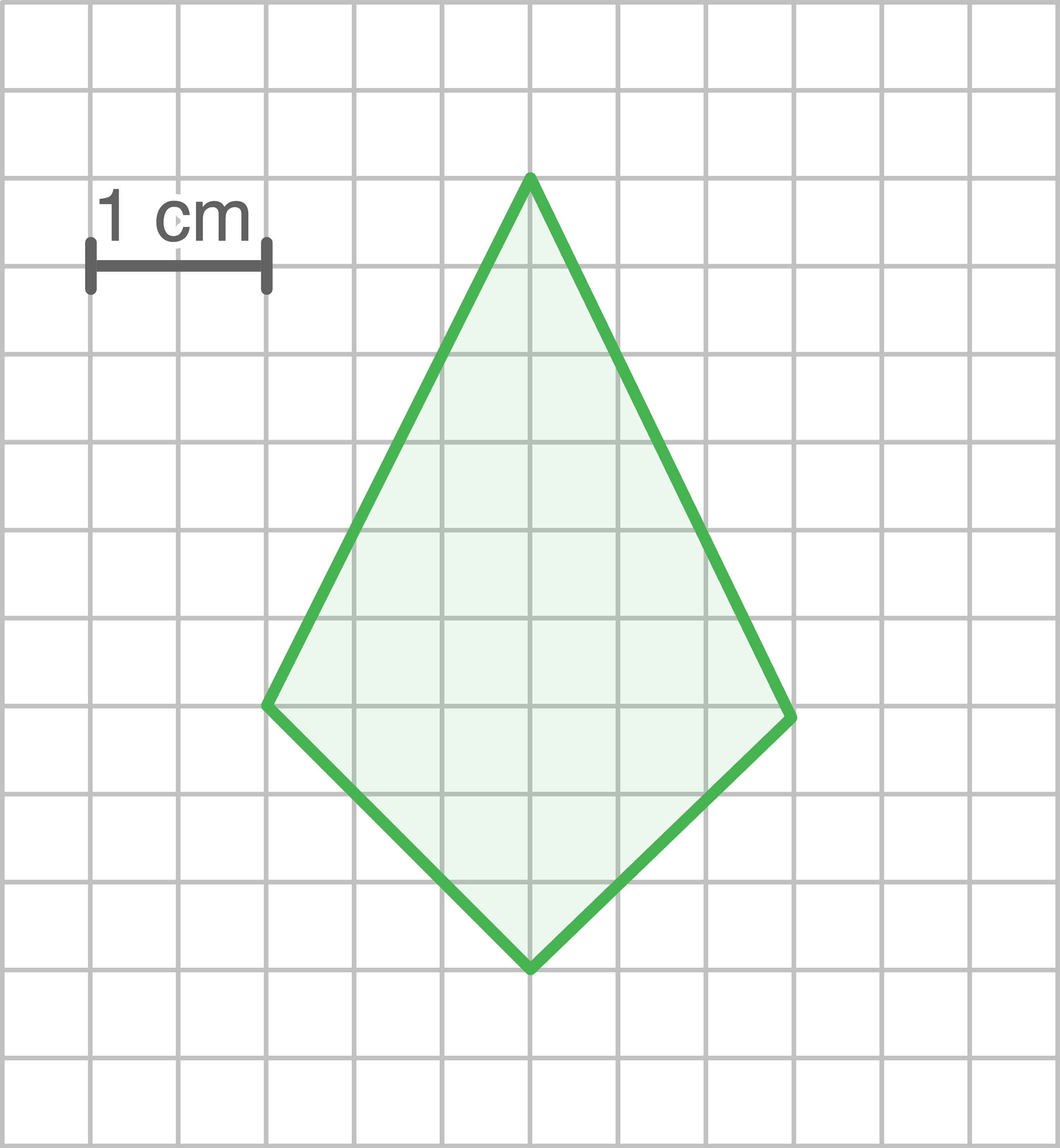
c)
Vergrößerungsfaktor: 
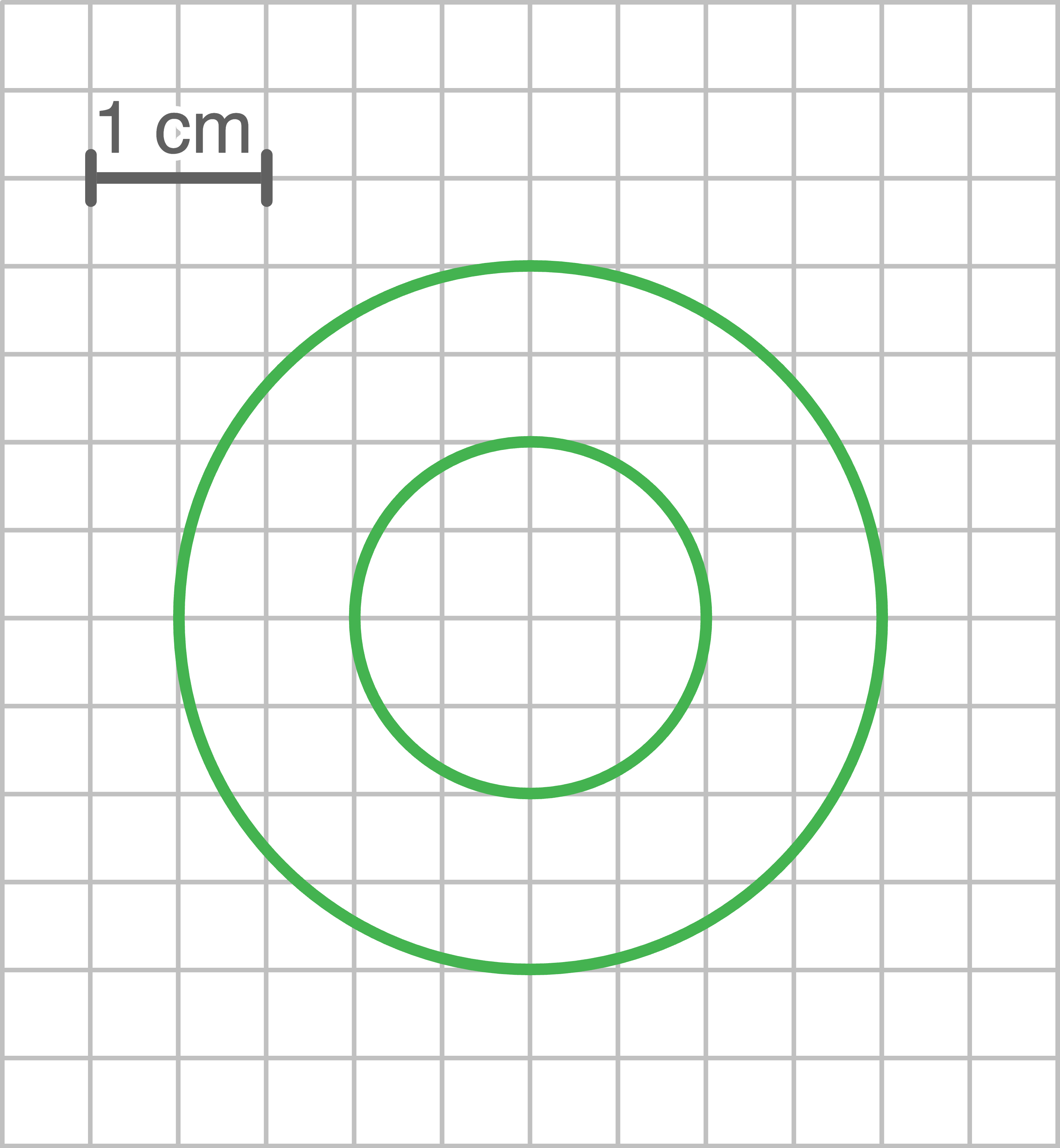
2
Sind die Figuren ähnlich? Begründe.
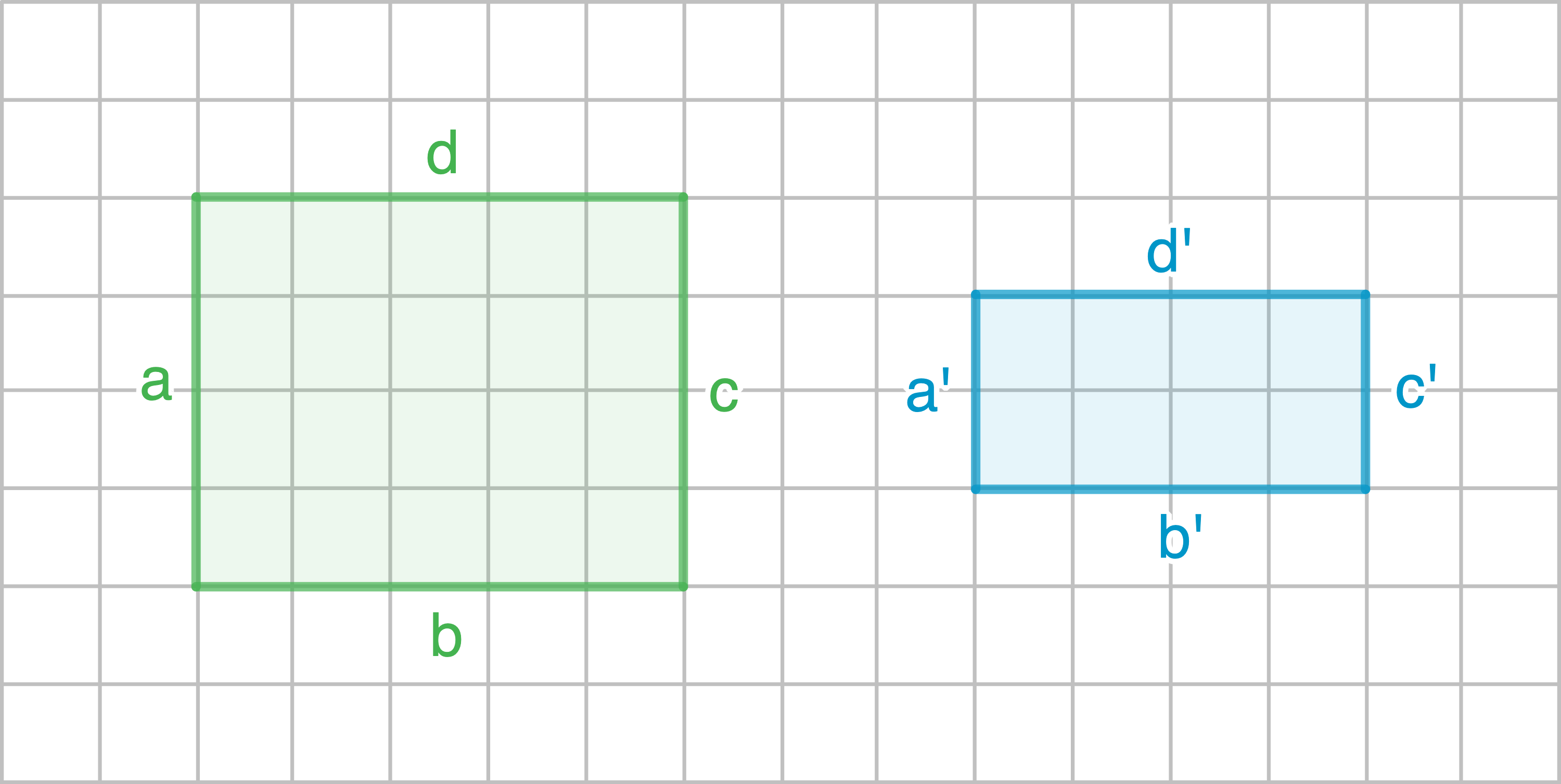
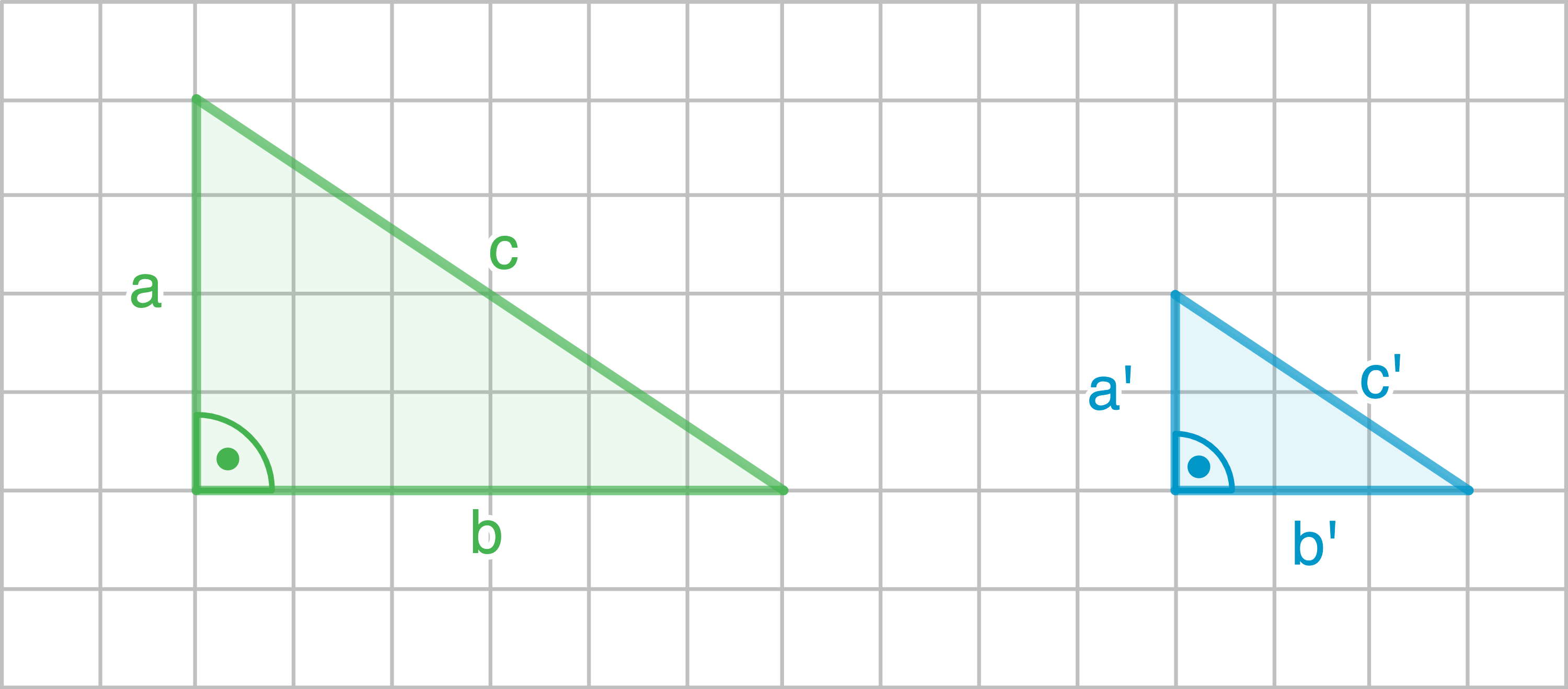
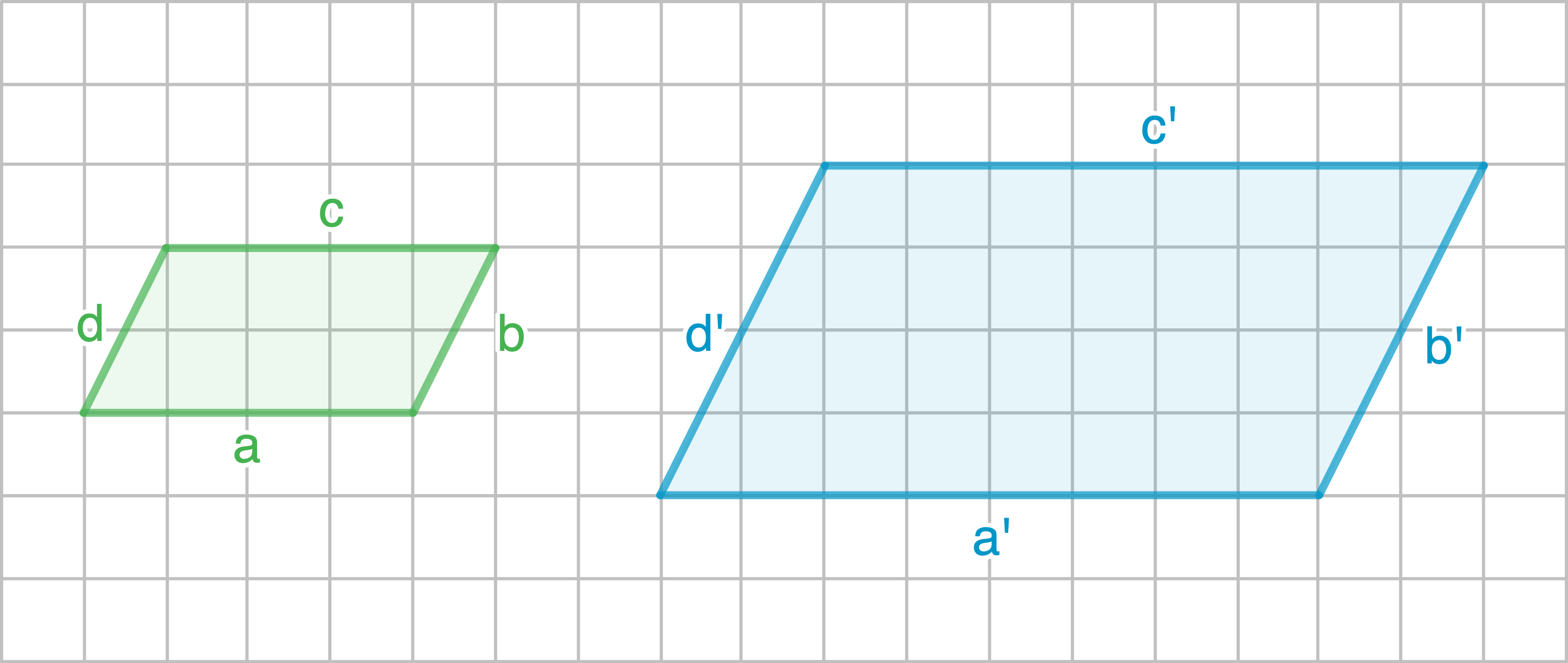
a)
b)
c)
3
Begründe, ob die Dreiecke jeweils ähnlich zueinander sind.
a)
Für das Dreieck 
gilt:
gilt:
b)
Für das Dreieck 
gilt:
gilt:
c)
Für das Dreieck 
gilt:
gilt:
d)
Für das Dreieck 
gilt:
gilt:
4
Für ein Rechteck gilt:
für welches bereits gegeben ist:
a)
Bestimme den Faktor 
b)
Zeichne das ähnliche Rechteck 
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
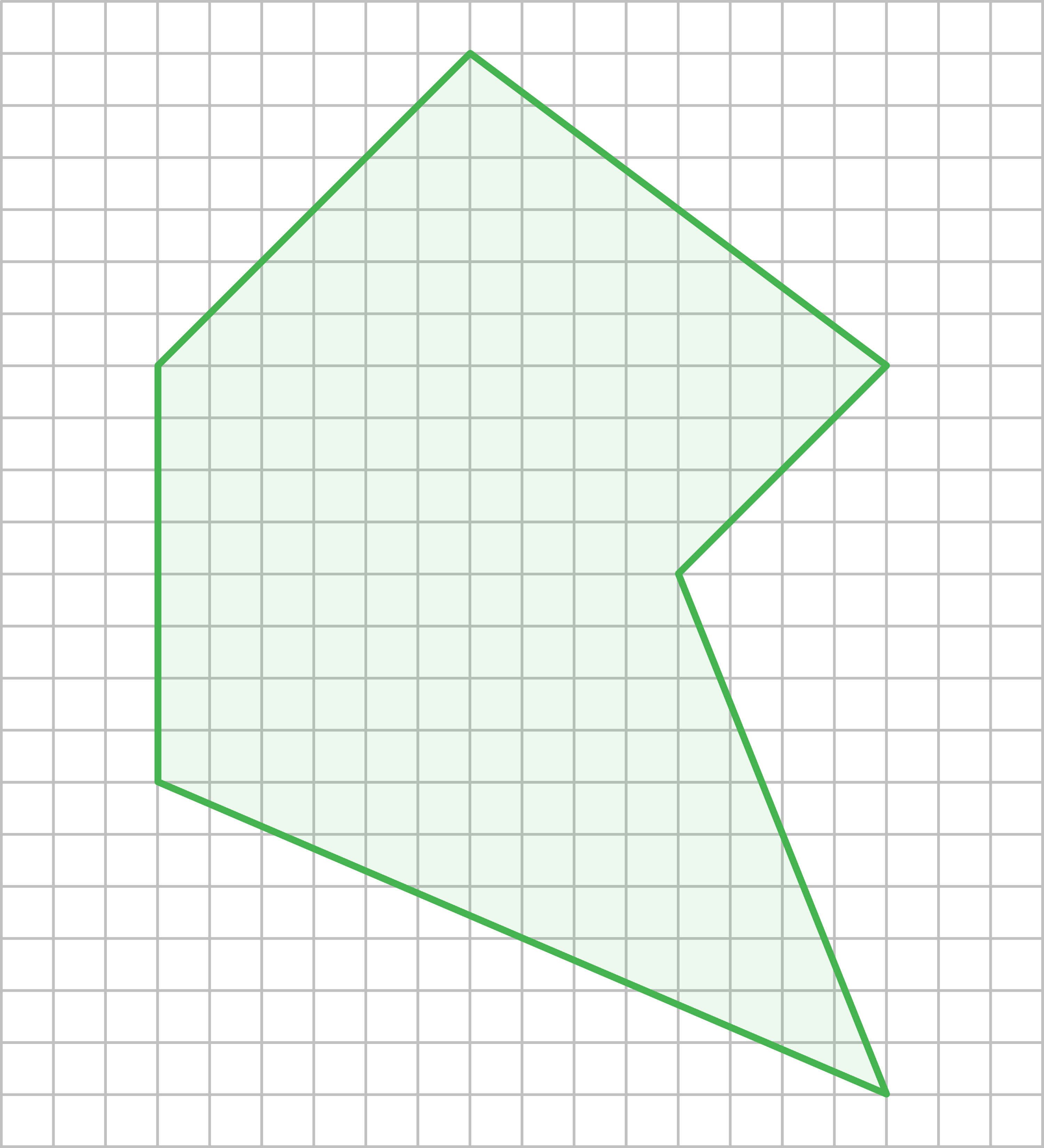
b)
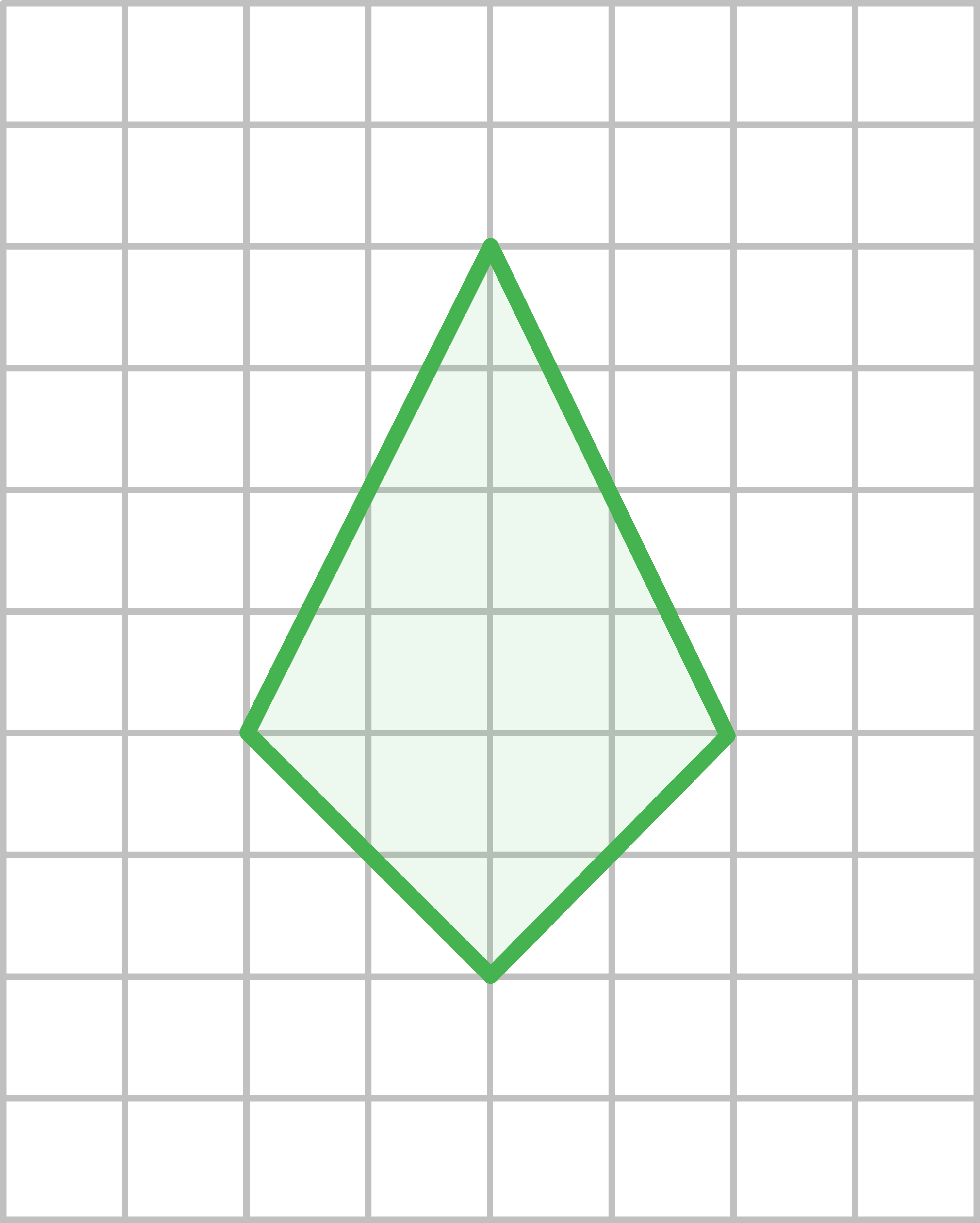
c)
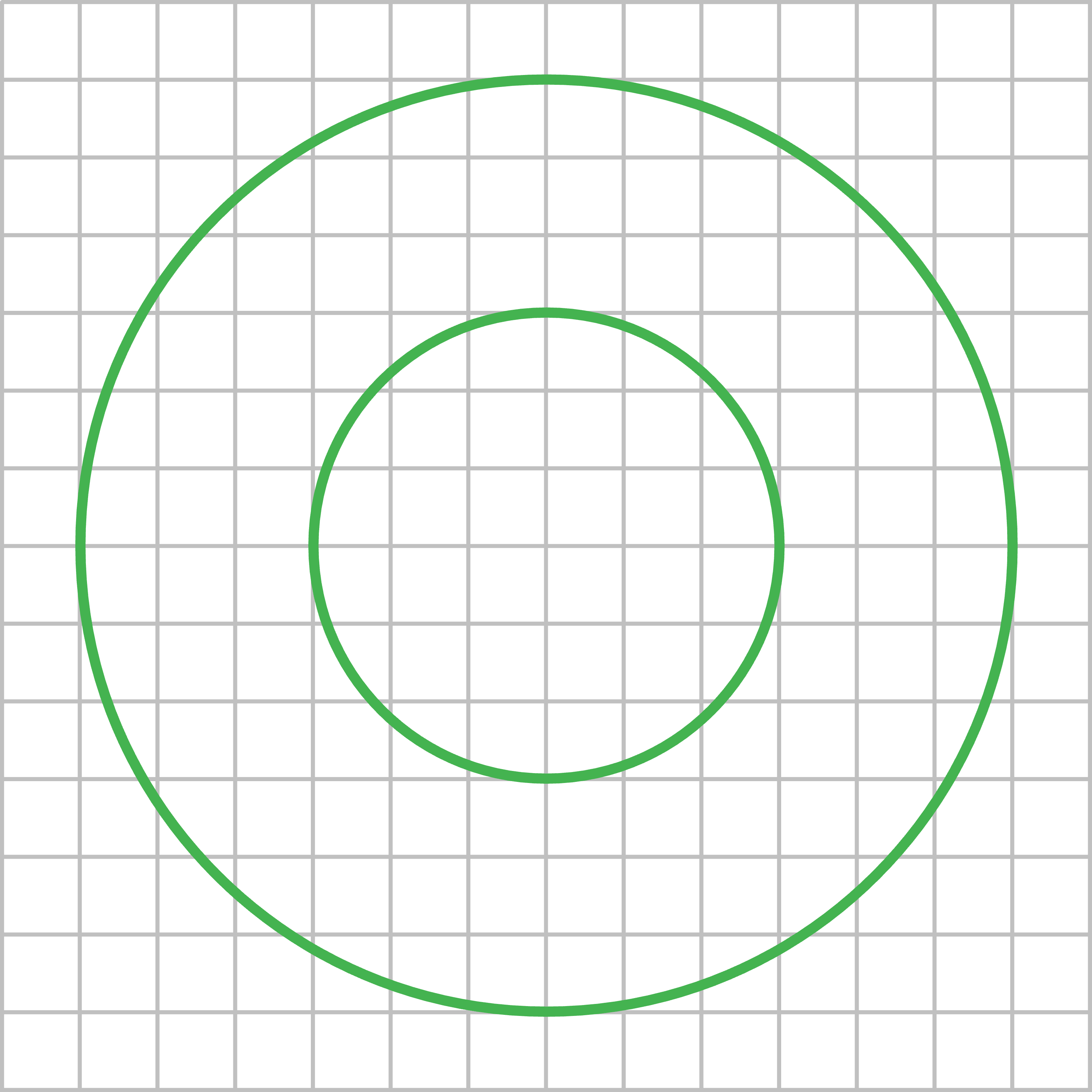
2
a)
Längenverhältnisse überprüfen:
Die Längenverhältnisse stimmen nicht überein.
Die Rechtecke sind nicht ähnlich.
b)
Längenverhältnisse überprüfen:
Um das Längenverhältnis der dritten Seite bestimmen zu können, müssen zunächst die Längen der Seite 
und der Seite 
mit dem Satz des Pythagoras berechnet werden:
![\(\begin{array}[t]{rll}
c^2&=&a^2+b^2 &\\[5pt]
c^2&=&2^2+3^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
c&=&\sqrt{2^2+3^2} &\\[5pt]
c&=&3,6 &\\[5pt]
\end{array}\)](https://mathjax.schullv.de/f78b94f3be81300b1d260d54c4901fe87221dd9c8838b2724a51bbc1dd4f59c1?color=5a5a5a)
![\(\begin{array}[t]{rll}
c](https://mathjax.schullv.de/7f0233e96c5450a42281ce3a3918313eab195b7586759a224e2d19bc5c7cc5b9?color=5a5a5a)
Somit folgt:
Die Längenverhältnisse stimmen überein.
Es gilt also: 
Die Rechtecke sind somit ähnlich.
c)
Längenverhältnisse überprüfen:
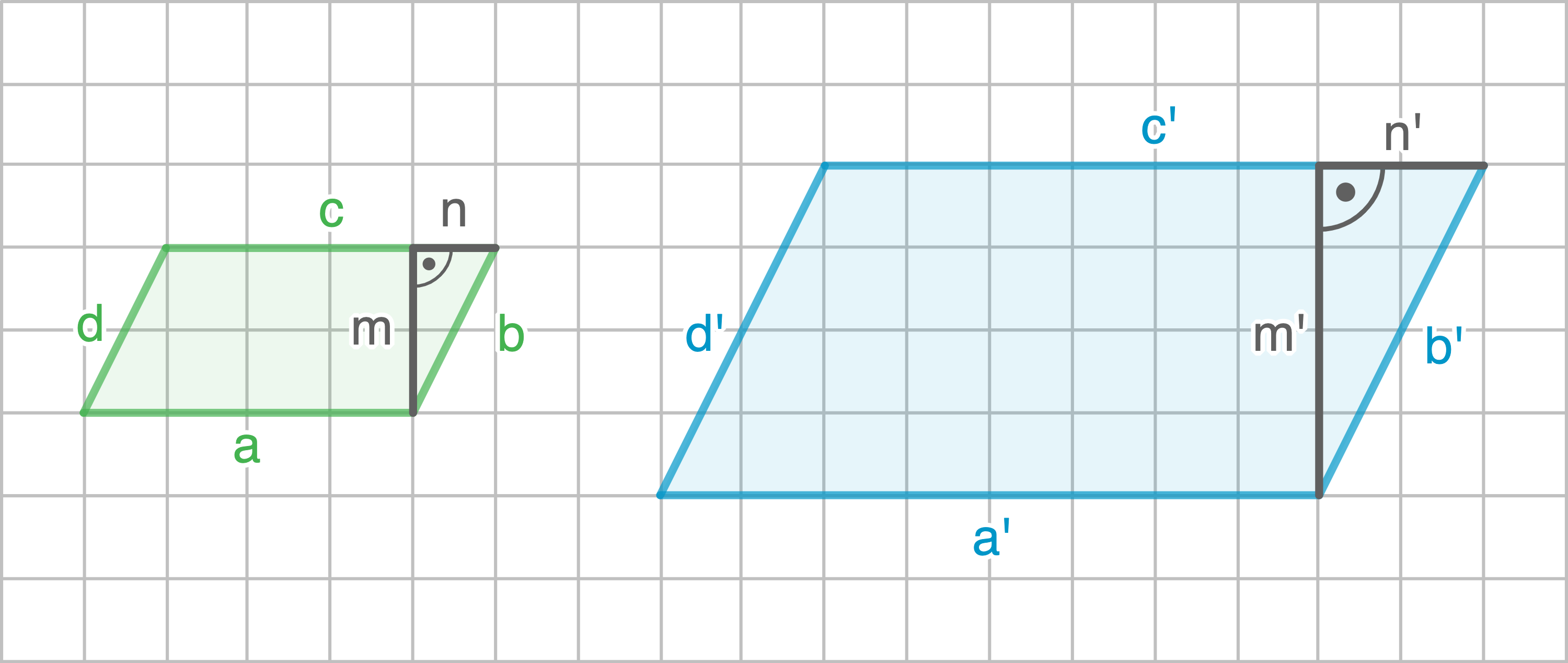Um das zweite Längenverhältnis bestimmen zu können, müssen zunächst die Längen der Seite 
und der Seite 
mit dem Satz des Pythagoras berechnet werden.
![\(\begin{array}[t]{rll}
b^2&=&m^2+n^2 &\\[5pt]
b^2&=&1^2+0,5^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
b&=&\sqrt{1^2+0,5^2} &\\[5pt]
b&=&1,1
\end{array}\)](https://mathjax.schullv.de/c1f4bff94c02fd6bccd94b5465908da764ff6f30c324b4ce0085730dc0d41d64?color=5a5a5a)
![\(\begin{array}[t]{rll}
b](https://mathjax.schullv.de/e7ef967b74a57649ec107260fec44cb5e2b01a68777a6ba44afd95c4772ff119?color=5a5a5a)
Es folgt also:
Da es sich bei beiden Figuren um Parallelogramme handelt, reicht das Überprüfen von zwei benachbarten Seiten aus.
Es gilt also: 
Die Parallelogramme sind ähnlich.
1
a)
Mit den Längenverhältnissen kann hier überprüft werden, ob die Dreiecke ähnlich sind.
Längenverhältnis 1
Längenverhältnis 2
Längenverhältnis 3
Da alle zusammengehörigen Seiten das gleiche Längenverhältnis haben, gilt: Die Dreiecke sind ähnlich.
b)
Mit den Winkelgrößen kann hier überprüft werden, ob die Dreiecke ähnlich sind.
Größe des Winkels 
![\(\begin{array}[t]{rll}
\gamma&=&180^{\circ}-\alpha-\beta &\\[5pt]
\gamma&=&180^{\circ}-35^{\circ}-90^{\circ} &\\[5pt]
\gamma&=&55^{\circ}&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/f8b4f60fa0192bc3b57b54a8ab49bc41e863e7621037001a4eab6e49b9824b41?color=5a5a5a)
Es gilt: 
Die Dreiecke sind nicht ähnlich.
c)
Mit den Seitenverhältnissen kann hier überprüft werden, ob die Dreiecke ähnlich sind.
Längenverhältnis 1
Längenverhältnis 2
Längenverhältnis 3
Das Längenverhältnis der Seiten und stimmt nicht mit dem Längenverhältnis der anderen Seiten überein. Somit gilt: Die Dreiecke sind nicht ähnlich.
d)
Mit den Winkelgrößen kann hier überprüft werden, ob die Dreiecke ähnlich sind.
Größe des Winkels 
![\(\begin{array}[t]{rll}
\alpha&=&180^{\circ}-\beta-\gamma &\\[5pt]
\alpha&=&180^{\circ}-83^{\circ}-36^{\circ} &\\[5pt]
\alpha&=&61^{\circ}&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/f8c92f5d917824da0bd68e6e3489adca6800e2e1da24ee145605592c8d11017b?color=5a5a5a)
Somit gilt: 
und 
Die Dreiecke sind also ähnlich.
4
a)
Da das Rechteck ähnlich zu Rechteck ist, gilt:
Somit gilt für den Faktor: 
b)
Länge der Seite berechnen:
