Ähnlichkeit bei Dreiecken
Definition
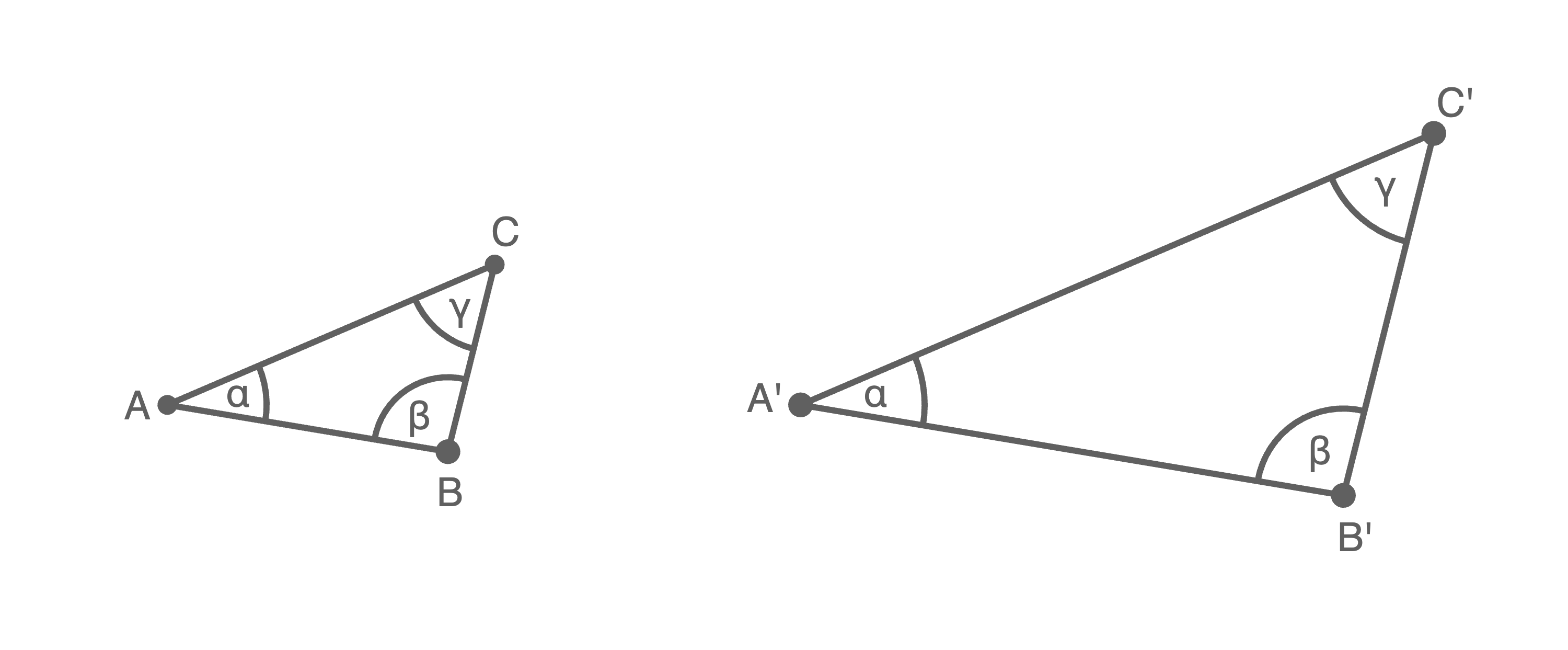
Anders als bei andere Figuren müssen zur Überprüfung der Ähnlichkeit bei Dreiecken nicht alle Seitenverhältnisse und Winkelgrößen verglichen werden. Mit den Eigenschaften der zentrischen Streckung und den Kongurenzsätzen für Dreiecke gilt: Hauptähnlichkeitssatz für Dreiecke Zwei Dreiecke sind ähnlich, wenn sie in der Größe zweier Winkel übereinstimmen (ww).Herleitung
Um zu prüfen, ob die Ähnlichkeit von zwei Dreiecken  und
und  festgestellt werden kann, wenn nur gegeben ist, dass die Winkelgrößen in beiden Dreiecken übereinstimmen, wird das Dreieck
festgestellt werden kann, wenn nur gegeben ist, dass die Winkelgrößen in beiden Dreiecken übereinstimmen, wird das Dreieck  mit einem Faktor
mit einem Faktor  zentrisch gestreckt, sodass eine Seite gleich groß wie die zugehörige Seite im Dreieck
zentrisch gestreckt, sodass eine Seite gleich groß wie die zugehörige Seite im Dreieck  ist.
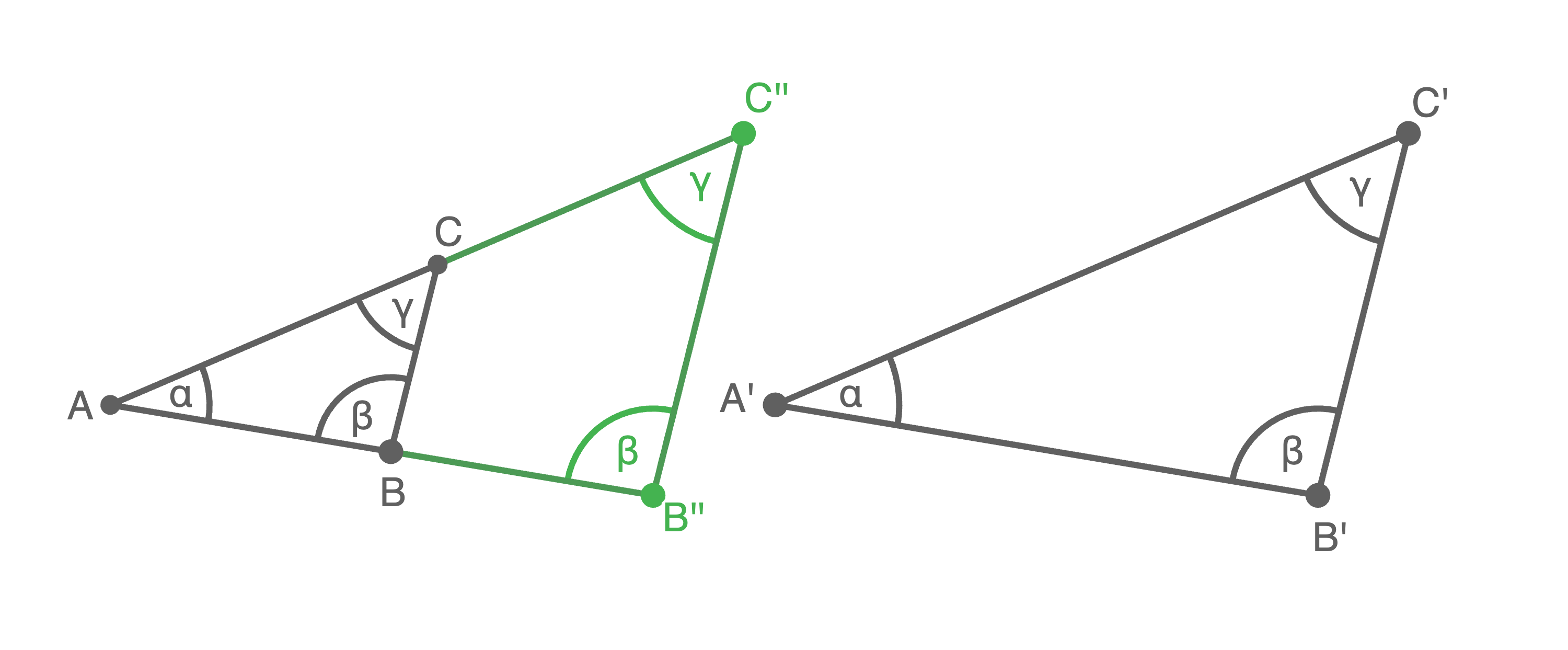
Da sich durch diese Streckung die Winkel nicht ändern, sind die Winkel des ursprünglichen und des gestreckten Dreiecks
ist.
Da sich durch diese Streckung die Winkel nicht ändern, sind die Winkel des ursprünglichen und des gestreckten Dreiecks  gleich. Da nun eine Seite gleich lang gewählt wurde und die Winkel in den Dreiecken
gleich. Da nun eine Seite gleich lang gewählt wurde und die Winkel in den Dreiecken  und
und  übereinstimmen, folgt mit dem Kongruenzsatz
übereinstimmen, folgt mit dem Kongruenzsatz  dass die beiden Dreiecke kongruent und somit insbesondere ähnlich sind.
Wenn zwei Dreiecke also gleiche Winkel haben, sind sie automatisch ähnlich. Da der dritte Winkel wegen der Innenwinkelsumme von
dass die beiden Dreiecke kongruent und somit insbesondere ähnlich sind.
Wenn zwei Dreiecke also gleiche Winkel haben, sind sie automatisch ähnlich. Da der dritte Winkel wegen der Innenwinkelsumme von  im Dreieck direkt folgt, müssen also nur zwei Winkel überprüft werden.
im Dreieck direkt folgt, müssen also nur zwei Winkel überprüft werden.
Weitere Ähnlichkeitssätze
Die gleiche Herleitung durch zentrische Streckung kann auch auf die Kongruenzsätze sss, sws und SsW angewandt werden, sodass weiterhin folgt: Zwei Dreiecke sind zueinander ähnlich, wenn sie...- in allen Verhältnissen einander entsprechender Seiten übereinstimmen (sss).
- in einem Winkel und den Verhältnissen einander entsprechender am Winkel anliegender Seiten übereinstimmen (sws).
- in einem Winkel und den Verhältnissen einander entsprechender am Winkel anliegender Seiten übereinstimmen oder in den Verhältnissen je zweier entsprechender Seiten und dem Gegenwinkel der jeweils größeren Seite übereinstimmen (SsW).
1
Prüfe, ob die beiden beschriebenen Dreiecke jeweils ähnlich sind und gib den passenden Ähnlichkeitssatz an.
a)
Dreieck 1:
 Dreieck 2:
Dreieck 2:

b)
Dreieck 1:
 Dreieck 2:
Dreieck 2:

c)
Dreieck 1:
 Dreieck 2:
Dreieck 2:

d)
Dreieck 1:
 Dreieck 2:
Dreieck 2:

e)
Dreieck 1 und Dreieck 2 sind jeweils rechtwinklig und gleichschenklig.
f)
Dreieck 1 und Dreieck 2 sind gleichseitig zueinander.
2
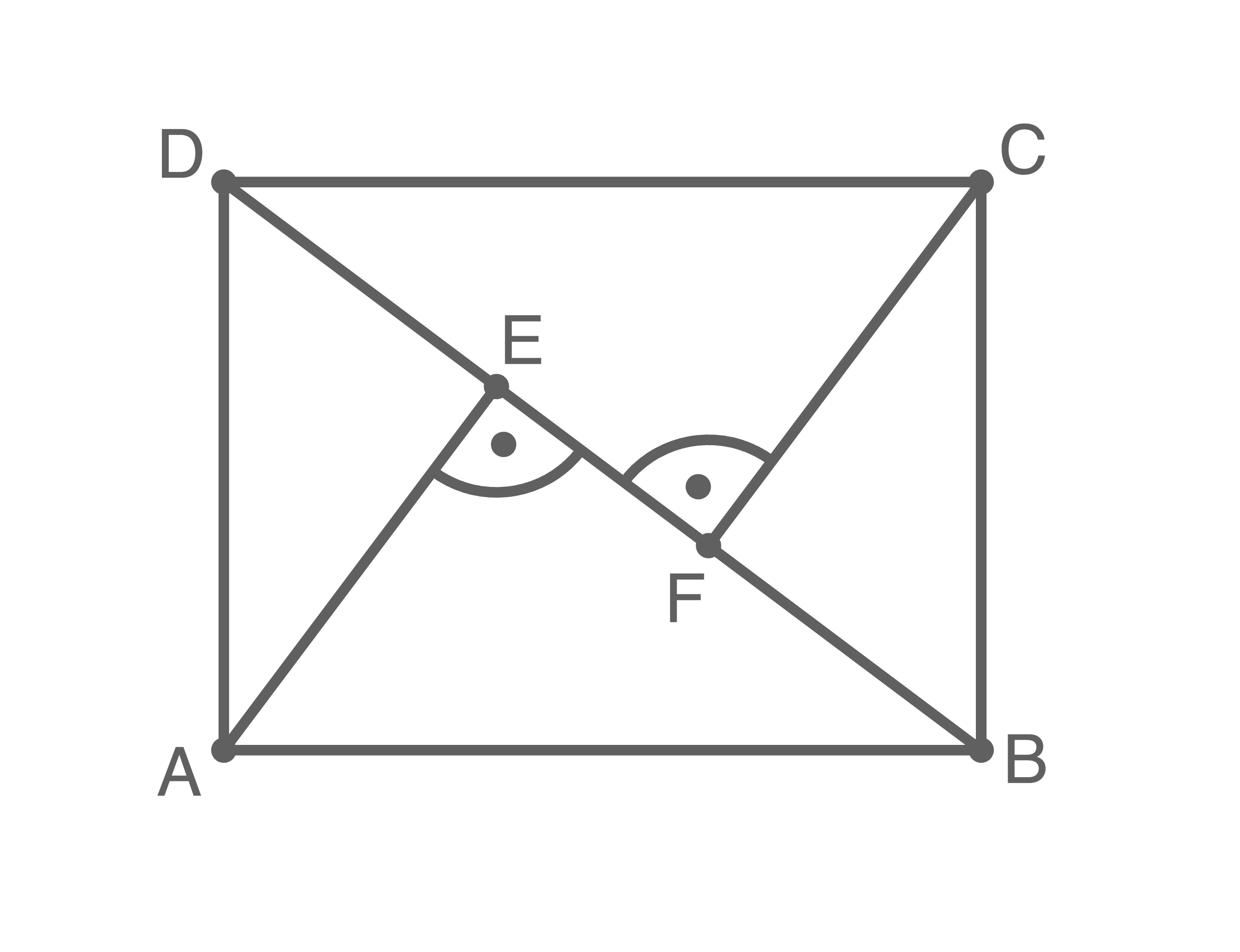
Ein Rechteck  hat die Seitenlängen
hat die Seitenlängen  und
und  . Durch das Einzeichnen der Diagonalen durch
. Durch das Einzeichnen der Diagonalen durch  und
und  sowie der zu dieser orthogonal stehenden Strecken von
sowie der zu dieser orthogonal stehenden Strecken von  und
und  aus ergeben sich vier Dreiecke.
aus ergeben sich vier Dreiecke.
a)
Prüfe, welche Dreiecke ähnlich zueinander sind und gib jeweils den entsprechenden Ähnlichkeitssatz an.
b)
Berechne die Länge der Diagonalen 
c)
Berechne jeweils die Seitenlängen der beiden Dreiecke  und
und 

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Mit dem Innenwinkelsatz ergibt sich der dritte Winkel des ersten Dreiecks zu:
![\(\begin{array}[t]{rlll}
\gamma&=& 180^\circ - \alpha -\beta & \\[5pt]
&=& 180^\circ - 80 ^\circ -30^\circ & \\[5pt]
&=& 70 ^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/fad98135c6889fce742009917ef33fb9967e0f7b6a77582c249cfbde014cf38c_light.svg) Somit stimmen zwei Winkelgrößen der beiden Dreiecke überein
Somit stimmen zwei Winkelgrößen der beiden Dreiecke überein  und
und  Nach dem Hauptähnlichkeitssatz (ww) sind die beiden Dreiecke also ähnlich.
Nach dem Hauptähnlichkeitssatz (ww) sind die beiden Dreiecke also ähnlich.
b)
Mit dem Innenwinkelsatz ergibt sich der dritte Winkel des ersten Dreiecks zu:
![\(\begin{array}[t]{rlll}
\gamma&=& 180^\circ - \alpha -\beta & \\[5pt]
&=& 180^\circ - 20 ^\circ -130^\circ & \\[5pt]
&=& 30 ^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/cbb7c991b497b5b3942e155e19abacb00b3862cb33c042f40ccff8d7c787c096_light.svg) Für das zweite Dreieck gilt:
Für das zweite Dreieck gilt:
![\(\begin{array}[t]{rlll}
\gamma&=& 180^\circ - \alpha -\beta & \\[5pt]
&=& 180^\circ - 30 ^\circ -120^\circ & \\[5pt]
&=& 30 ^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/970825ef2d7803863f0dc840247f0652c4c2201b667f5591eac0e650311e600a_light.svg) Somit stimmen die beiden Dreiecke in keiner Winkelgröße überein.
Die Dreiecke sind somit nicht ähnlich.
Somit stimmen die beiden Dreiecke in keiner Winkelgröße überein.
Die Dreiecke sind somit nicht ähnlich.
c)
Um entsprechende Seiten zu vergleichen, muss das Verhältnis der kleinsten Seite von Dreieck 1 zur kleinsten Seite von Dreieck 2 verglichen werden und analog für alle weiteren Seiten vorgegangen werden:


 Mit dem Ähnlichkeitssatz sss sind die beiden Dreiecke somit ähnlich.
Mit dem Ähnlichkeitssatz sss sind die beiden Dreiecke somit ähnlich.
d)
Es wird analog wie in c) vorgegangen, um die Seitenverhältnisse zu bestimmen:


 Die beiden Dreiecke sind somit nicht ähnlich.
Die beiden Dreiecke sind somit nicht ähnlich.
e)
Da beide Dreiecke rechtwinklig sind, folgt direkt, dass sie eine gemeinsame Winkelgröße haben  Wegen der Gleichschenkligkeit muss außerdem gelten, dass die Schenkelwinkel jeweils gleichgroß sind und mit der Innenwinkelsumme des Dreiecks somit jeweils
Wegen der Gleichschenkligkeit muss außerdem gelten, dass die Schenkelwinkel jeweils gleichgroß sind und mit der Innenwinkelsumme des Dreiecks somit jeweils  Mit dem Hauptähnlichkeitssatz (ww) sind die beiden Dreiecke somit ähnlich.
Mit dem Hauptähnlichkeitssatz (ww) sind die beiden Dreiecke somit ähnlich.
f)
In einem gleichseitigen Dreieck sind per Definition alle drei Winkel gleich groß  Da die Winkel also in beiden Dreiecken übereinstimmen, sind die Dreiecke nach dem Hauptähnlichkeitssatz für Dreiecke (ww) ähnlich.
Da die Winkel also in beiden Dreiecken übereinstimmen, sind die Dreiecke nach dem Hauptähnlichkeitssatz für Dreiecke (ww) ähnlich.
2
a)
Es ergeben sich sechs Dreiecke:

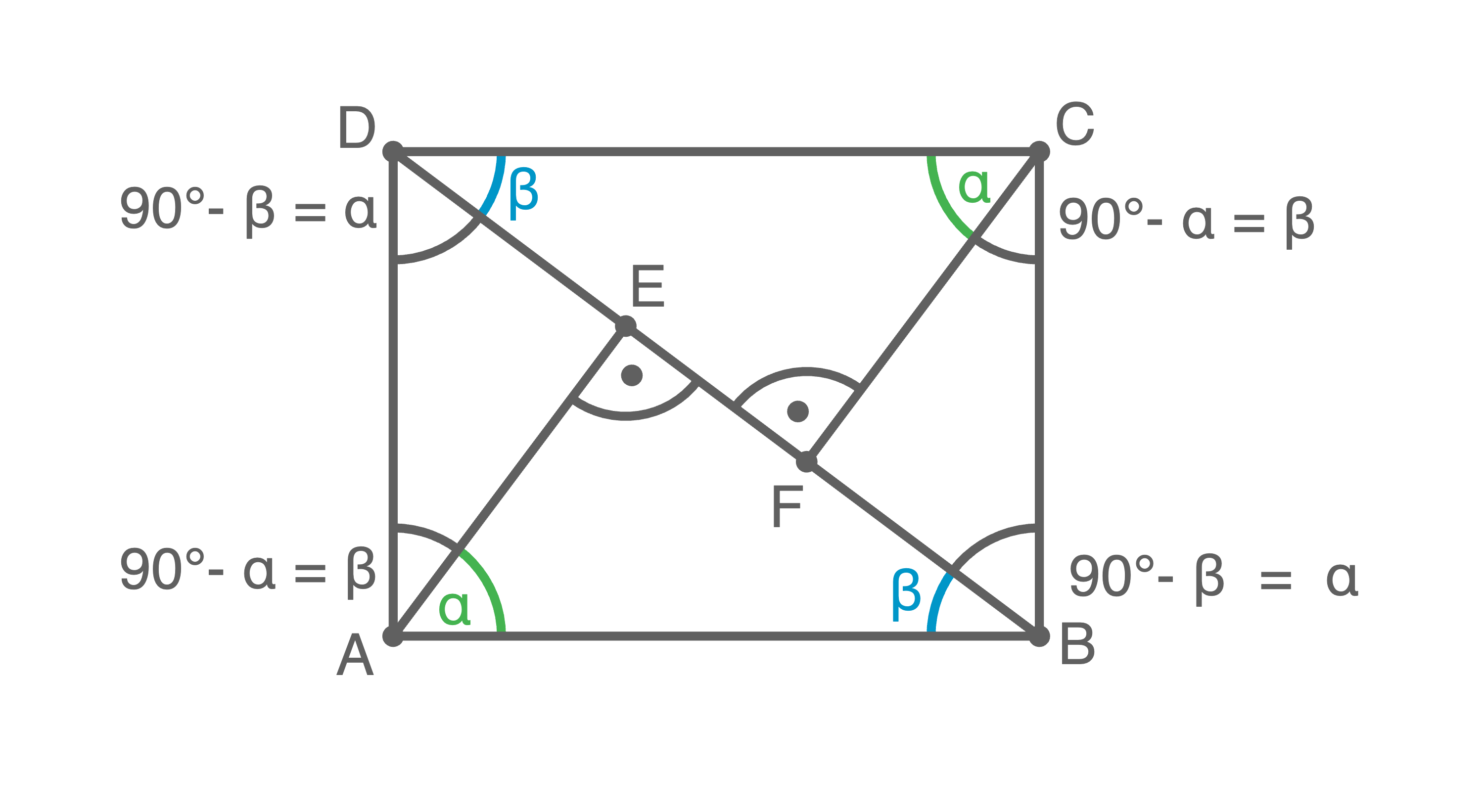
- Da die gegenüberliegenden Seiten im Rechteck gleich lang sind, gilt mit sws, dass
und
ähnlich sind
- Mit dem Wechselwinkelsatz an der Diagonalen gilt, dass der Winkel bei
im Dreieck
gleich groß ist wie der Winkel bei
im Dreieck
Da beide Dreiecke außerdem einen rechten Winkel besitzen, sind die beiden Dreiecke mit dem Hauptähnlichkeitssatz ww ähnlich.
- Mit der gleichen Begründung sind die beiden Dreiecke
und
ähnlich.
- Da jede Ecke im Rechteck
hat, gilt für den Winkel bei
im Dreieck
Analog gilt für den Winkel bei
Somit stimmen sich die Dreiecke
und
in allen Winkeln überein. Mit dem Hauptähnlichkeitssatz ww folgt also die Ähnlichkeit.
- Mit der gleichen Begründung sind die beiden Dreiecke
und
ähnlich.
- Da sich die beiden Dreiecke
und
den Winkel bei
teilen und jeweils einen rechten Winkel besitzen, sind die beiden Dreiecke mit mit dem Hauptähnlichkeitssatz ww ähnlich.
- Mit der gleichen Begründung sind die beiden Dreiecke
und
ähnlich.
b)
Mit dem Satz des Pythagoras gilt:
![\(\begin{array}[t]{rlll}
DB^2 &=& 9^2 + 12 ^2&\\[5pt]
DB^2 &=& 225 &\mid\; \sqrt{\, }\\[5pt]
DB&=& 15
\end{array}\)](https://www.schullv.de/resources/formulas/f596e08ceebd16ebb9f450e516ddf556e23e3690f2d030a773771d1e353faef2_light.svg)
c)
Seitenlängen von AED
Die Diagonale  des Dreiecks
des Dreiecks  entspricht der Grundseite
entspricht der Grundseite  des Dreiecks
des Dreiecks  Diese sind gegeben und stehen im Verhältnis
Diese sind gegeben und stehen im Verhältnis  zueinander.
Die Höhe
zueinander.
Die Höhe  des Dreiecks
des Dreiecks  entspricht der Seite
entspricht der Seite  des Dreiecks
des Dreiecks  Mit dem gegebenen Längenverhältnis gilt also:
Mit dem gegebenen Längenverhältnis gilt also:
![\(\begin{array}[t]{rlll}
\frac{5}{3}&=& \frac{AD}{DE} &\mid\; AD= 9\\[5pt]
\frac{5}{3}&=& \frac{9}{DE} &\mid\; \cdot DE\\[5pt]
\frac{5}{3}\cdot DE&=& 9 &\mid\; \cdot \frac{3}{5}\\[5pt]
DE &=& 5,4
\end{array}\)](https://www.schullv.de/resources/formulas/412887dcd8fd8cd1bbcf05bb686add11cc173506602a35c0ea73e1805b882df6_light.svg) Für die dritte Seite gilt analog:
Für die dritte Seite gilt analog:
![\(\begin{array}[t]{rlll}
\frac{5}{3}&=& \frac{AB}{AE} &\mid\; AB= 12\\[5pt]
\frac{5}{3}&=& \frac{12}{AE} &\mid\; \cdot AE\\[5pt]
\frac{5}{3}\cdot AE&=& 12 &\mid\; \cdot \frac{3}{5}\\[5pt]
AE &=& 7,2
\end{array}\)](https://www.schullv.de/resources/formulas/23ac75b614d1ec950ce4d45a152816f4489a9bbd727d7a0ad479c6654baed3b1_light.svg) Das Dreieck
Das Dreieck  besitzt somit die Seitenlängen
besitzt somit die Seitenlängen  und
und  Seitenlängen von ABE
Die Diagonale
Seitenlängen von ABE
Die Diagonale  des Dreiecks
des Dreiecks  entspricht der Grundseite
entspricht der Grundseite  des Dreiecks
des Dreiecks  Diese sind gegeben und stehen im Verhältnis
Diese sind gegeben und stehen im Verhältnis  zueinander.
Die Höhe
zueinander.
Die Höhe  des Dreiecks
des Dreiecks  entspricht der Seite
entspricht der Seite  des Dreiecks
des Dreiecks  Diese ist bereits berechnet worden und entspricht 7,2. Mit dem gegebenen Längenverhältnis kann dies überprüft werden:
Diese ist bereits berechnet worden und entspricht 7,2. Mit dem gegebenen Längenverhältnis kann dies überprüft werden:
![\(\begin{array}[t]{rlll}
\frac{5}{4}&=& \frac{AD}{AE} &\mid\; AD= 9\\[5pt]
\frac{5}{4}&=& \frac{9}{AE} &\mid\; \cdot AE\\[5pt]
\frac{5}{4}\cdot AE&=& 9 &\mid\; \cdot \frac{4}{5}\\[5pt]
DE &=& 7,2
\end{array}\)](https://www.schullv.de/resources/formulas/c83e6671a85089883fa99d7a2f16f653de1f2127f1973a10ec1d5004d3009a90_light.svg) Für die dritte Seite gilt analog:
Für die dritte Seite gilt analog:
![\(\begin{array}[t]{rlll}
\frac{5}{4}&=& \frac{AB}{EB} &\mid\; AB= 12\\[5pt]
\frac{5}{4}&=& \frac{12}{EB} &\mid\; \cdot EB\\[5pt]
\frac{5}{4}\cdot EB&=& 12 &\mid\; \cdot \frac{4}{5}\\[5pt]
EB &=& 9,6
\end{array}\)](https://www.schullv.de/resources/formulas/e5511c09d6e8047ffd7e2526fb1b6510bf360989803bd0cb198d1b8a70c5ea97_light.svg) Das Dreieck
Das Dreieck  besitzt somit die Seitenlängen
besitzt somit die Seitenlängen  und
und 