Gleichungen höheren Grades
Gleichungen dritten Grades
Gleichungen dritten Grades besitzen folgende Form:Biquadratische Gleichungen
Biquadratische Gleichungens besitzen folgende Form:
Beispiel
![\(\begin{array}[t]{rlll}
x^3+2x^2-3x&=& 0 &\mid\; \text{Ausklammern} \\[5pt]
x\cdot (x^2+2x-3)&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/4ba2e3e8a74b173b02c77990ec6bd8388559df2391d8048afddf20015bb765b5_light.svg) Mit dem Satz vom Nullprodukt folgt direkt
Mit dem Satz vom Nullprodukt folgt direkt  sowie
sowie  Anwenden der
Anwenden der  -Formel ergibt:
-Formel ergibt:
![\(\begin{array}[t]{rlll}
x_{2;3}&=& -\dfrac{2}{2} \pm \sqrt{\left(\dfrac{2}{2}\right)^2-(-3)} \\[5pt]
x_{2;3}&=& -1 \pm \sqrt{4} \\[5pt]
x_2&=& -5 & \\[5pt]
x_3&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/3adae8abfedc47d32bee871e3aca204b4adabf862a93fd83d9d5ccf42849aa9b_light.svg) Lösungsmenge:
Lösungsmenge: 
Beispiel
 Substitution mit
Substitution mit  ergibt:
ergibt:
 Anwenden der
Anwenden der  -Formel ergibt nun:
-Formel ergibt nun:
![\(\begin{array}[t]{rlll}
x_{1;2}&=& -\dfrac{8}{2} \pm \sqrt{\left(\dfrac{8}{2}\right)^2-7} \\[5pt]
x_{1;2}&=& 4 \pm \sqrt{9} \\[5pt]
x_1&=& 1 & \\[5pt]
x_2&=& 7
\end{array}\)](https://www.schullv.de/resources/formulas/9bdc17b2c4f4dcce2cb7f971e21e6d96b1238cd8046ee935cf6e66fd66a303bd_light.svg) Rücksubstitution ergibt:
Rücksubstitution ergibt:
![\(\begin{array}[t]{rlll}
z&=& x^2 &\mid\;z_1=1 \\[5pt]
1&=& x^2 &\mid\; \sqrt{\,} \\[5pt]
\pm 1 &=& x
\end{array}\)](https://www.schullv.de/resources/formulas/a57c1e08f0ed1e5522a6a45ae0815c8aeeec2fcb56bd22f1419508731f91566c_light.svg)
![\(\begin{array}[t]{rlll}
z&=& x^2 &\mid\;z_2=7 \\[5pt]
7&=& x^2 &\mid\; \sqrt{\,} \\[5pt]
\pm \sqrt{7} &=& x
\end{array}\)](https://www.schullv.de/resources/formulas/ede48a4d04ebd3ba0bcb3e1fe332bc1f65b8d915981ce66295d92924a5a42f29_light.svg) Lösungsmenge:
Lösungsmenge: 
1
Löse die Gleichungen.






a)
b)
c)
d)
e)
f)
2
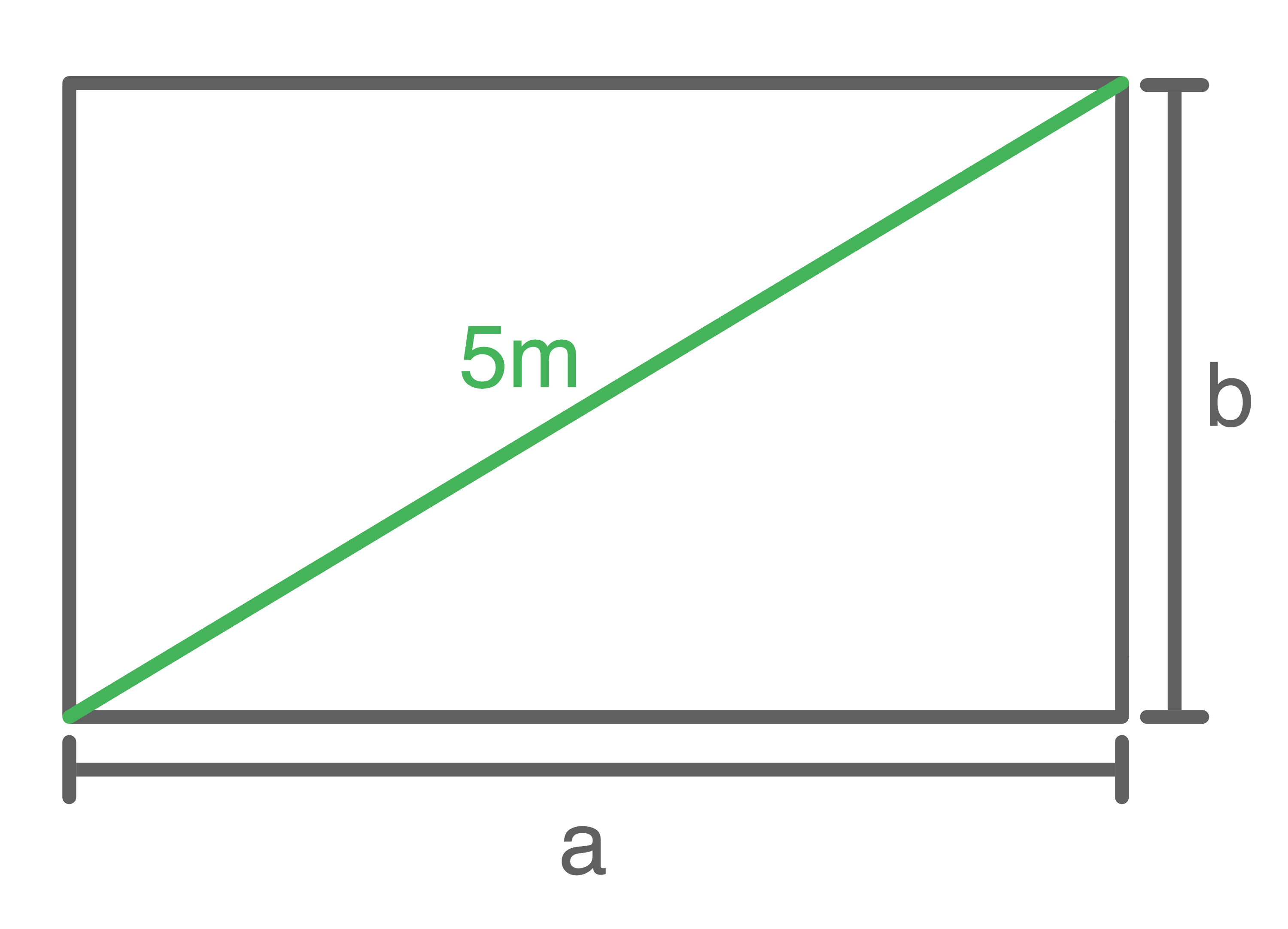
In einem Rechteck mit dem Flächeninhalt  ist die Diagonale
ist die Diagonale  lang.
Berechne die Seitenlängen des Rechtecks.
lang.
Berechne die Seitenlängen des Rechtecks.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
d)
Substitution mit  ergibt:
ergibt:
 Anwenden der
Anwenden der  -Formel ergibt nun:
-Formel ergibt nun:
![\(\begin{array}[t]{rlll}
x_{1;2}&=& -\dfrac{(-6)}{2} \pm \sqrt{\left(\dfrac{-6}{2}\right)^2-5} \\[5pt]
x_{1;2}&=& 3 \pm \sqrt{4} \\[5pt]
x_1&=& 1 & \\[5pt]
x_2&=& 5
\end{array}\)](https://www.schullv.de/resources/formulas/cf21414bdd5c6e3644cda4985b587118eb9a56836f0a28a06441d42327b12419_light.svg) Rücksubstitution ergibt:
Rücksubstitution ergibt:
![\(\begin{array}[t]{rlll}
z&=& x^2 &\mid\;z_1=1 \\[5pt]
1&=& x^2 &\mid\; \sqrt{\,} \\[5pt]
\pm 1 &=& x
\end{array}\)](https://www.schullv.de/resources/formulas/a57c1e08f0ed1e5522a6a45ae0815c8aeeec2fcb56bd22f1419508731f91566c_light.svg)
![\(\begin{array}[t]{rlll}
z&=& x^2 &\mid\;z_2=5 \\[5pt]
5&=& x^2 &\mid\; \sqrt{\,} \\[5pt]
\pm \sqrt{5} &=& x
\end{array}\)](https://www.schullv.de/resources/formulas/b24e4eb27a08c4dbc158201fc061355e68d45eaac46d516d60178e16b64430c7_light.svg) Lösungsmenge:
Lösungsmenge: 
e)
f)
2
1. Schritt: Funktionsgleichung aufstellen
Für die Längen  und
und  der Seiten des Rechtecks gilt:
der Seiten des Rechtecks gilt:
![\(\begin{array}[t]{rll}
a\cdot b&=& 12 &\quad \scriptsize \mid\; :a\\[5pt]
b&=&\dfrac{12}{a}
\end{array}\)](https://www.schullv.de/resources/formulas/e7e3c3a80c1f7401cadc4e2299d674e7ac9dbf279e5dde617453f580d30183df_light.svg) Einsetzen in die dritte Bedingung liefert nun:
Einsetzen in die dritte Bedingung liefert nun:
![\(\begin{array}[t]{rll}
a^2+\left(\dfrac{12}{a}\right)^2&=& 5^2& \\[5pt]
a^2+\dfrac{144}{a^2}&=& 25&\quad \scriptsize \mid\; \cdot a^2\\[5pt]
a^4+144&=& 25a^2&\quad \scriptsize \mid\; -25a^2\\[5pt]
a^4-25a^2+144&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/c166da3d0d74ac1375b68df1295024de97fcc2260917c5b73387c5b8897bce41_light.svg) 2. Schritt: Substitution
Mit
2. Schritt: Substitution
Mit  folgt:
folgt:
 3. Schritt: Quadratische Gleichung lösen
Mit der
3. Schritt: Quadratische Gleichung lösen
Mit der  -Formel ergibt sich:
-Formel ergibt sich:
![\(\begin{array}[t]{rlll}
x_{1;2}&=&-\dfrac{(-25)}{2} \pm \sqrt{\left(\dfrac{-25}{2}\right)^2-144} \\[5pt]
x_{1;2}&=& 12,5 \pm 3,4 & \\[5pt]
x_1&=& 9 &\\[5pt]
x_2&=& 16
\end{array}\)](https://www.schullv.de/resources/formulas/6bb9f6297d6cb2d87a434b52e75e7e805e5ed43070e1382e292f67c4a84b6560_light.svg) 4. Schritt: Resubstitution
Ersetzen von
4. Schritt: Resubstitution
Ersetzen von  durch
durch  liefert:
liefert:
![\(\begin{array}[t]{rll}
a^2&=& z_1& \mid z_1=9 \\[5pt]
a^2&=& 9 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
a&=& \pm 3
\end{array}\)](https://www.schullv.de/resources/formulas/926df74c3a240230e30d5f017a1c802fa43dbc4c0be039c4f0623643f1c4e087_light.svg)
![\(\begin{array}[t]{rll}
a^2&=& z_2& \mid z_2=16\\[5pt]
a^2&=& 16&\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
a&=& \pm 4
\end{array}\)](https://www.schullv.de/resources/formulas/e6ae2d649dc6f80d8bb8636cfe8caaaee288465c6b24fba995ef922edb411b98_light.svg) Da
Da  gelten muss, kommen nur die positiven Lösungen
gelten muss, kommen nur die positiven Lösungen  und
und  als eine Seitenlänge des Rechtecks in Betracht.
5. Schritt: Gleichung lösen
als eine Seitenlänge des Rechtecks in Betracht.
5. Schritt: Gleichung lösen
![\(\begin{array}[t]{rll}
a\cdot b&=& 12&\quad \scriptsize \mid\; a_1=3\\[5pt]
3\cdot b&=& 12&\quad \scriptsize \mid\; :3\\[5pt]
b&=& 4
\end{array}\)](https://www.schullv.de/resources/formulas/7065113e6740daccc492347c0c201daaa9be955db19f49841e3af635e86cc554_light.svg)
![\(\begin{array}[t]{rll}
a\cdot b&=& 12&\quad \scriptsize \mid\; a_2=4\\[5pt]
4\cdot b&=& 12&\quad \scriptsize \mid\; :4 \\[5pt]
b&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/0333c9f9ebbca95f0fb6f60d97a62ada6d4402a2bef9dcae742cbe6c53e895a8_light.svg) Die Seitenlängen des Rechtecks betragen somit
Die Seitenlängen des Rechtecks betragen somit  und
und 