Parabeln
Das Schaubild der quadratischen Funktion 
ist eine Parabel.
Der höchste bzw. tiefste Punkt einer solchen Parabel wird Scheitelpunkt genannt und hat die Koordinaten 
Die Parabel wird um den Koeffizienten 
gestreckt oder gestaucht. Das Vorzeichen des Koeffizienten 
bestimmt hierbei, ob die Parabel nach oben oder nach unten geöffnet ist.
Die Parabel zur Funktionsgleichung 
mit 
heißt Normalparabel.
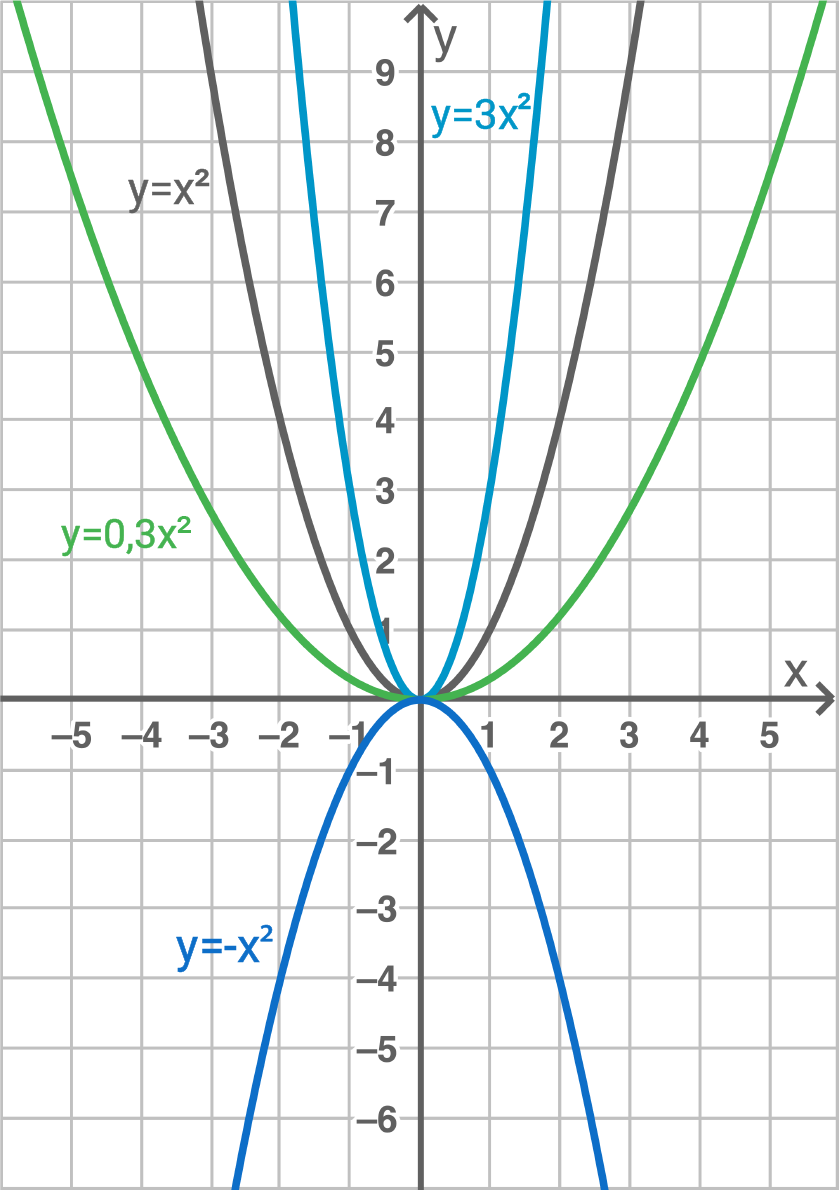
Öffnung der Parabel:
Parabel ist nach oben geöffnet
Parabel ist nach unten geöffnet
- Für
oder
ist die Parabel schmaler als die Normalparabel.
- Liegt
und
ist die Parabel breiter als die Normalparabel, ebenso wenn
und
1
Überprüfe rechnerisch, ob die gegebenen Punkte auf der Parabel 
liegen.
a)
b)
c)
d)
2
Bestimme denjenigen Wert von 
für den die Parabel der Form 
durch den Punkt 
verläuft, und zeichne den Graphen in ein Koordinatensystem.
a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Punktprobe durch Einsetzen der Koordinaten von 
in die gegebene quadratische Funktion ergibt:
![\(\begin{array}[t]{rlll}
6&=& 1,5\cdot 2^2 & \\[5pt]
6&=& 1,5\cdot 4 & \\[5pt]
6&=& 6
\end{array}\)](https://mathjax.schullv.de/a917ab78dd94e06b43273c06562be534302ae87774377b9111aa67e8d22ab70c?color=5a5a5a)
Da die Koordinaten von die Gleichung erfüllen, liegt auf der Parabel.
b)
Punktprobe:
![\(\begin{array}[t]{rlll}
-1,5&=& 1,5\cdot (-1)^2 & \\[5pt]
-1,5&=& 1,5\cdot 1 & \\[5pt]
-1,5&=& 1,5
\end{array}\)](https://mathjax.schullv.de/4cb4149f66f7cc3e14af96dd0eae1a3524b08d2c01916f79cf8eb4d6fa2047ed?color=5a5a5a)
Da die Koordinaten von 
die Gleichung nicht erfüllen, liegt nicht auf der Parabel.
c)
Punktprobe:
![\(\begin{array}[t]{rlll}
22&=& 1,5\cdot 4^2 & \\[5pt]
22&=& 1,5\cdot 16 & \\[5pt]
22&=& 24
\end{array}\)](https://mathjax.schullv.de/d37c99c8130f7bd521d2943ca6d3378c7e1e28f519d3d1d34d6a19d3656d53d7?color=5a5a5a)
Da die Koordinaten von 
die Gleichung nicht erfüllen, liegt nicht auf der Parabel.
d)
Punktprobe:
![\(\begin{array}[t]{rlll}
13,5&=& 1,5\cdot (-3)^2 & \\[5pt]
13,5&=& 1,5\cdot 9 & \\[5pt]
13,5&=& 13,5
\end{array}\)](https://mathjax.schullv.de/3369bbda8286c211a2fbf09a7a77ab896b0d382847bd5c030989cebec30c143a?color=5a5a5a)
Da die Koordinaten von 
die Gleichung erfüllen, liegt auf der Parabel.
2
a)
Einsetzen der Koordinaten von in die gegebene Parabelform liefert:
![\(\begin{array}[t]{rlll}
y&=& a\cdot x^2 &\quad \mid\; (1 \mid 4) \\[5pt]
4&=& a\cdot 1^2 &\quad \mid\; :1 \\[5pt]
4&=& a
\end{array}\)](https://mathjax.schullv.de/bffa53e2995f03a4fe67dc90f525bdada3598e4c3b872631b96f5f05454331ee?color=5a5a5a)
Die Parabel verläuft somit für den Wert 
durch den Punkt 
b)
c)
d)