Laplace-Experiment
Ein Laplace-Experiment ist ein Zufallsexperiment, bei dem alle möglichen Ergebnisse mit der gleichen Wahrscheinlichkeit erzielt werden. Für die Wahrscheinlichkeit eines Ereignisses 
gilt bei einem Laplace-Experiment die folgende Merkregel:
Jede Karte kommt nur einmal vor, das heißt alle Karten besitzen die gleiche Wahrscheinlichkeit aufgedeckt zu werden. Insgesamt gibt es fünf mögliche Karten, auf denen sich der Mond befinden könnte. Von diesen ist aber nur auf einer wirklich der Mond aufgedruckt. Somit folgt für die Wahrscheinlichkeit des Ereignisses 
„Der Mond wird nicht aufgedeckt“:
Beispiel
Auf den abgebildeten Karten, von denen bereits eine umgedreht ist, ist jeweils ein Symbol eines Himmelskörpers zu sehen. Es kommt keine Karte doppelt vor und unter den verdeckten Karten befindet sich unter anderem eine, die mit dem Mond bedruckt ist.
Bestimme die Wahrscheinlichkeit, dass beim einmaligen Aufdecken einer Karte nicht der Mond zum Vorschein kommt.
Bestimme die Wahrscheinlichkeit, dass beim einmaligen Aufdecken einer Karte nicht der Mond zum Vorschein kommt.
1
Eine Geldmünze mit den Seiten „Kopf“ und „Zahl“ wird vier Mal geworfen. Berechne die Wahrscheinlichkeiten für die folgenden Ereignisse:
„Kopf und Zahl werden gleich oft geworfen“
„Es wird mindestens ein Mal Zahl geworfen“
a)
b)
c)
2
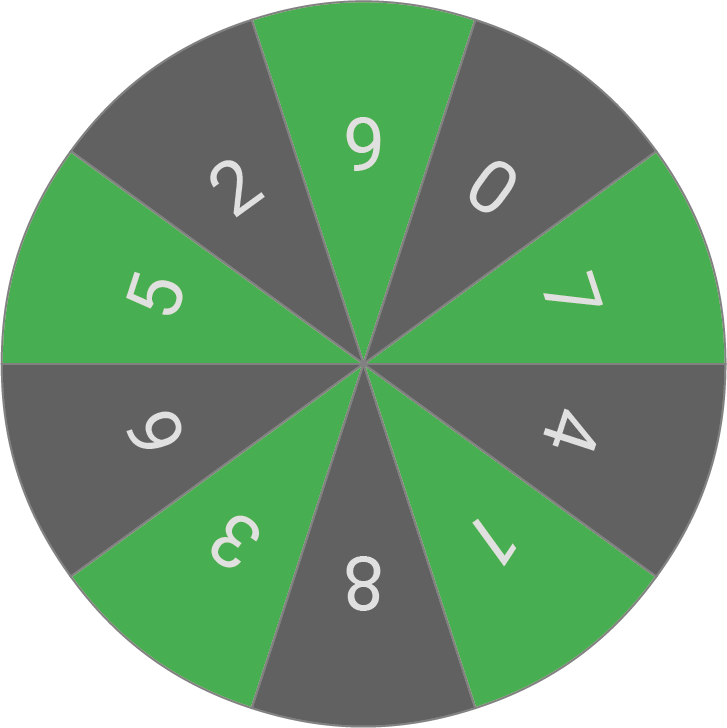
Auf einem Stadtfest gibt es einen Stand mit einem Glücksrad, das mit den Zahlen 
bis 
beschriftet ist. Der Einsatz für das Drehen des Glücksrades beträgt 
und nach jeder Drehung erhält der Spieler einen Eurobetrag in Höhe der gedrehten Zahl.
Überprüfe rechnerisch, ob die Wahrscheinlichkeit bei zweimaligem Drehen des Glücksrades Gewinn zu machen, mehr als
beträgt.
Überprüfe rechnerisch, ob die Wahrscheinlichkeit bei zweimaligem Drehen des Glücksrades Gewinn zu machen, mehr als
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Jedes Mal, wenn die Münze geworfen wird, gibt es zwei mögliche Ergebnisse: Kopf und Zahl. Somit ergibt sich die insgesamte Anzahl der möglichen Ergebnisse nach viermaligem Werfen der Münze als 
Aus der Mengenschreibweise der Ereignisses lässt sich leicht ablesen, dass zu genau zwei Ergebnisse gehören. Somit folgt:
b)
Ereignis 
tritt ein, wenn sowohl Kopf als auch Zahl jeweils zwei Mal geworfen werden. Hierfür gibt es mehrere Möglichkeiten: Kopf kann in Wurf 1 und 2, Wurf 1 und 3, Wurf 1 und 4, Wurf 2 und 3, Wurf 2 und 4 oder Wurf 3 und 4 geworfen werden. Das sind also insgesamt sechs verschiedene Möglichkeiten, die zwei Mal Kopf auf die insgesamt 4 Würfe aufzuteilen. Mit der Formel für die Wahrscheinlichkeiten von Ereignissen eines Laplace-Experiments folgt somit:
c)
Es wird immer mindestens ein Mal Zahl geworfen, außer wenn in jedem der vier Würfe Kopf fällt. Somit liefern 
der 
möglichen Ergebnisse das Ereignis 
Damit folgt für die gesuchte Wahrscheinlichkeit:
2
Um bei einem Einsatz von pro Drehung Gewinn zu machen, muss die Summe der beiden erzielten Zahlen über 
liegen. Wenn das Ereignis, dessen Wahrscheinlichkeit gesucht ist, mit 
bezeichnet wird, gilt somit in Mengenform:
Es gehören somit Ergebnisse zu dem Ereignis 
Insgesamt können 
verschiedene Ergebnisse durch zwei Drehungen erzielt werden. Damit folgt für die Wahrscheinlichkeit von 
Die Wahrscheinlichkeit, bei zweimaligem Drehen des Glücksrades einen Gewinn zu erzielen, beträgt somit nicht mehr als 